- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Круги Ейлера
Содержание
- 2. 621811+57ІІІХІХ9VI:ІХХI3IIV=
- 3. Множина—це сукупність різних об'єктів, які об'єднуються за певною спільною ознакою.
- 4. Леонардо Ейлер
- 5. Типи кругів Ейлера
- 6. ЩGЇЖБФКАВОSZFVQLT
- 7. Задача 1За святковим столом сиділо 15 дітей.
- 8. 5 + 8 = 13 дітей, що
- 9. Задача 2У класі навчається 14 дівчат. П'ять
- 10. 5 + 3 = 8 дівчат, які
- 11. Задача 3У групі зі 100 туристів 70
- 12. 100704523
- 13. Задача 4У класі 35 учнів. У математичному
- 15. З 90 туристів, що відправляються в подорож,
- 16. 3Англійською та французькою мовами володіють 10 людей,
- 17. німецькийфранцузькийанглійський375Відомо, що німецькою мовою володіють 30 людей,
- 18. Задача 6В одному з відділів магазину покупці
- 19. тортицукерки573612
- 20. Задача 7На уроці літератури вчитель спробував дізнатися,
- 21. 32СВ25222233А3110
- 23. 24, 129, 3, 57, 10, 1352410312913557
- 24. 924, 137, 80, 101, 1030, 5400809241371011030540
- 25. 9237, 101, 103092371011030
- 26. Скачать презентацию
- 27. Похожие презентации























Слайд 7
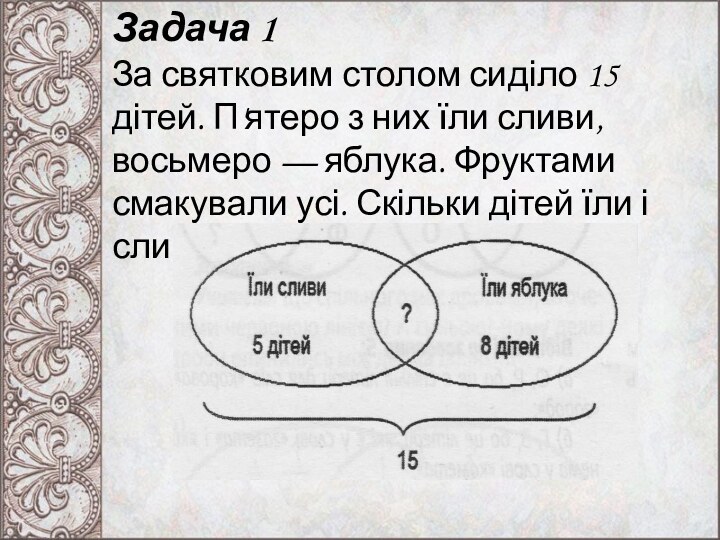
Задача 1
За святковим столом сиділо 15 дітей. П'ятеро
з них їли сливи, восьмеро — яблука. Фруктами смакували
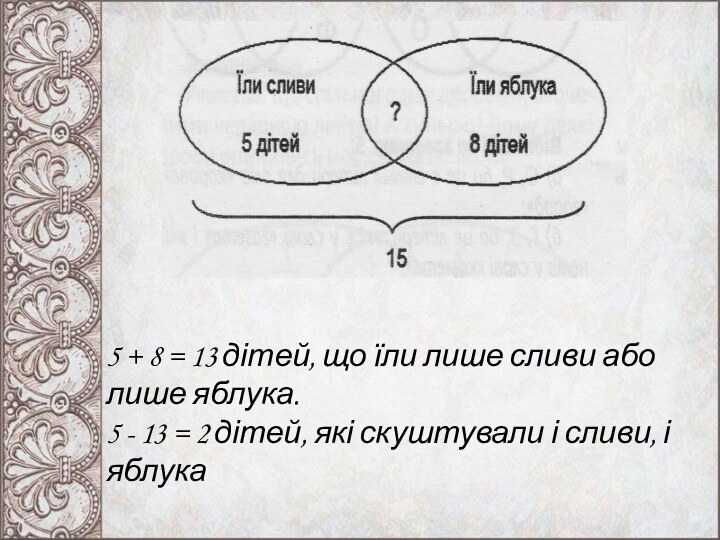
усі. Скільки дітей їли і сливи, і яблука?Слайд 8 5 + 8 = 13 дітей, що їли
лише сливи або лише яблука.
5 - 13 =
2 дітей, які скуштували і сливи, і яблука
Слайд 9
Задача 2
У класі навчається 14 дівчат. П'ять із
них відвідують лише гурток в'язання, а три — і
гурток в'язання, і гурток вишивання. Скільки дівчат відвідують лише гурток вишивання?Слайд 10 5 + 3 = 8 дівчат, які відвідували
гурток в'язання.
14 - 8 = 6 дівчат, які
відвідували лише гурток вишивання.
Слайд 11
Задача 3
У групі зі 100 туристів 70 знають
англійську мову, 45 – французьку і 23 –знають обидві мови. Скільки туристів
у групі не знають ні англійської, ні французької?
Слайд 13
Задача 4
У класі 35 учнів. У математичному гуртку
з них 12 займаються, в біологічному - 9, а
16 хлопців не відвідують ці гуртки. Скільки біологів захоплюються математикою.Слайд 14
35
Б-9
М - 12
Розв'язання. Виконуємо рисунок. Кількість учнів зобразимо за допомогою великого кола, а всередині помістимо кола поменше.
35 - 16 = 19 хлопців - займаються в гуртках
19 - 12 = 7 - біологи, які не відвідують мат. гурток
19 - 12 = 7 – біологи, які не відвідують мат. гурток
Слайд 15 З 90 туристів, що відправляються в подорож, німецькою
мовою володіють 30 людей, англійською - 28, французькою -
42. Англійською та німецькою одночасно володіють 8 людей, англійською та французькою -10, німецькою та французькою - 5, всіма трьома мовами - 3. Скільки туристів не володіють жодною мовою?Розв’язання:
Покажемо умову задачі графічно - за допомогою трьох кіл
французька
німецька
англійська
30
28
42
8
10
5
3
Задача 5
Слайд 16
3
Англійською та французькою мовами володіють 10 людей, а
3 з них володіють ще й німецькою. Значить, англійською
та французькою володіють 10 - 3 = 7 (людей)німецька
французька
англійська
У загальну частину англійської та французької кіл вписуємо число 7
7
Англійською та німецькою мовами володіють 8 чоловік, а 3 з них володіють ще і французьким. Значить, англійською і німецькою володіють 8 - 3 = 5 (людей)
У загальну частину англійської та німецької кіл вписуємо число 5
5
німецька
французька
английська
30
42
28
8
10
5
3
Слайд 17
німецький
французький
англійський
3
7
5
Відомо, що німецькою мовою володіють 30 людей, але
5 + 3 + 2 = 10 з них
володіють і іншими мовами, значить, тільки німецький знають 20 чоловік.Англійська мова знають 28 людина, але 5 + 3 + 7 = 15 чоловік володіють та іншими мовами, значить, тільки англійську знають 13 чоловік. Французьку мову знають 42 людини, але 2 + 3 + 7 = 12 чоловік володіють та іншими мовами, значить, тільки французький знають 30 чоловік. За умовою задачі всього 90 туристів. 20 + 30 + 13 + 5 + 2 + 3 + 7 = 80 туристів знають хоча б одну мову, отже, 10 людина не володіють жодною мовою.Німецькою та французькою мовами володіють 5 осіб, а 3 з них володіють ще й англійською. Значить, німецькою та французькою володіють
5 - 3 = 2 (людини)
У загальну частину німецької та французької кіл вписуємо число 2
2
20
13
30
Відповідь. 10 осіб.





























