- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Лекция № 2. Числовые характеристики выборки
Содержание
- 2. Выборочное среднее. Выборочная дисперсия. Выборочное среднее квадратическое
- 3. Пусть дано статистическое распределение выборки объёма n:где m – число ваиантов.
- 4. Выборочным средним
- 5. Выборочной дисперсией называется
- 6. Особенность состоит в том,
- 7. Выборочные начальные и центральные моменты. Асимметрия. Эксцесс.Приведём
- 8. Начальным выборочным моментом порядка называется среднее арифметическое
- 9. Из определения следует, что центральный выборочный момент второго порядка :
- 10. Выборочным коэффициентом асимметрии называется число
- 11. Выборочным коэффициентом эксцесса или коэффициентом крутости называется
- 12. Вычисление числовых характеристик выборки
- 13. -середина интервалов;
- 14. Упрощённый способ вычисления статистических характеристик вариационных рядовПри
- 15. Для вычисления числовых характеристик выборки составляем таблицуКонтроль:
- 16. С помощью сумм, полученных в нижней строке
- 17. Пример. Вычислить числовые характеристики выборки, рассмотренной в
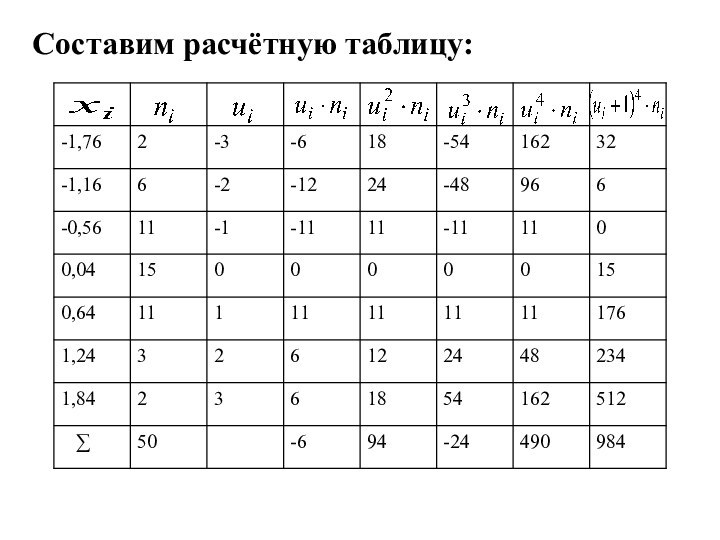
- 18. Составим расчётную таблицу:
- 19. Контроль:
- 20. Скачать презентацию
- 21. Похожие презентации
Выборочное среднее. Выборочная дисперсия. Выборочное среднее квадратическое отклонение В теории вероятностей определили числовые характеристики для случайных величин, с помощью которых можно сравнивать однотипные случайные величины. Аналогично можно определить ряд числовых характеристик и для выборки.


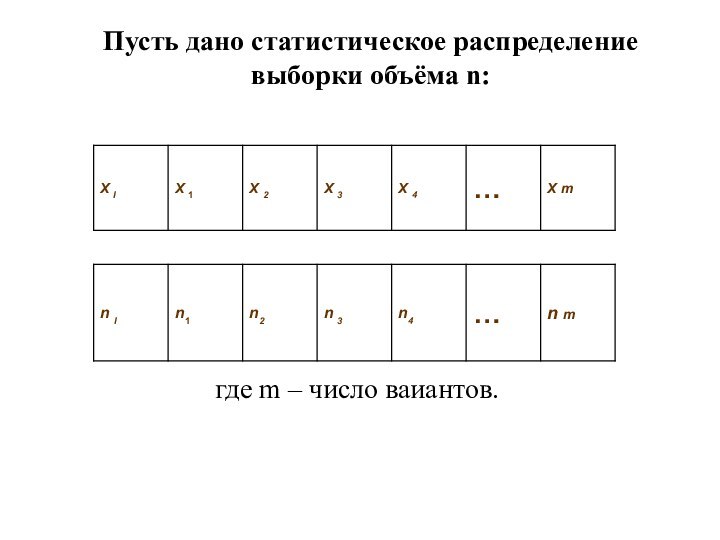
















Слайд 4 Выборочным средним называется
среднее арифметическое всех значений выборки.
Выборочное среднее можно записать и
так: , где:- частость.
В случае интервального статистического ряда в качестве берут середины интервалов, а ni – соответствующие им частоты.
Слайд 5 Выборочной дисперсией называется среднее
арифметическое квадратов отклонений выборки от
выборочного
среднего :или
Выборочное среднее квадратическое выборки определяется формулой:
Слайд 6 Особенность состоит в том, что
оно измеряется в тех же единицах, что и данные
выборки.Если объём выборки мал ( ), то пользуются исправленной выборочной дисперсией:
Величина называется исправленным средним квадратическим отклонением.
Слайд 7
Выборочные начальные и центральные моменты. Асимметрия. Эксцесс.
Приведём краткий
обзор характеристик, которые наряду с уже рассмотренными применяются для
анализа статистических рядов и являются аналогами соответствующих числовых характеристик случайной величины.Среднее выборочное и выборочная дисперсия являются частным случаем более общего понятия – момента статистического ряда.
Слайд 8 Начальным выборочным моментом порядка называется среднее арифметическое l
– х-степеней всех значений выборки:
или .Из определения следует , что начальный выборочный момент первого порядка:
Центральным выборочным моментом порядка l называется среднее арифметическое l-х-степеней отклонений наблюдаемых значений выборки от выборочного среднего .
или
Слайд 10
Выборочным коэффициентом асимметрии называется
число
, определяемое формулой:
Выборочный коэффициент асимметрии служит для
характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из его ветвей, начиная с вершины, имеет больший «спуск», чем другая.Если , то более пологий «спуск» полигона наблюдается слева; если - справа. В первом случае асимметрию называют левосторонней, а во втором – правосторонней.
Слайд 11 Выборочным коэффициентом эксцесса или коэффициентом крутости называется число
, определяемое формулой:
.
Выборочный коэффициент эксцесса служит для сравнения на «крутость» выборочного распределения с нормальным распределением. Коэффициент эксцесса для случайной величины, распределённой по нормальному закону, равен 0.
Поэтому за стандартное значение выборочного эксцесса принимают . Если , то полигон имеет более пологую вершину по сравнению с нормальной кривой ; если
, то полигон более крутой по сравнению с нормально кривой.
Слайд 13
-середина интервалов;
- частоты;
- объём выборки; с помощью суммы находимс помощью суммы находим и
с помощью суммы находим
С помощью суммы находим
Слайд 14
Упрощённый способ вычисления статистических характеристик вариационных рядов
При больших
значениях вариантов и соответствующих им частот вычисление выборочного среднего,
дисперсии и выборочного моментов по приведённым ниже формулам приводит к громоздким вычислениям.В этом случае условные варианты , определяемые по формулам ,
где числа с и h выбираются произвольно. Чтобы упростить вычисления, в качестве с выбирают вариант, который имеет наибольшую частоту или находится в середине ряда. Число с называется «ложным нулём». В качестве h выбирают число равное длине интервала (в случае интервального ряда) или наибольший общий делитель разностей .
Слайд 16 С помощью сумм, полученных в нижней строке таблицы,
находим условные моменты:
Числовые характеристики выборки вычисляем по формулам:
где
и находим по формулам:Слайд 17 Пример. Вычислить числовые характеристики выборки, рассмотренной в примере
2.
В качестве вариантов возьмём середины интервалов.
Перейдём
к условным вариантам.Вариант, значение которого 0,04, имеет наибольшую частоту и находится в середине модального ряда. Примем его за «ложный ноль» (начало отсчёта).
Условные варианты найдём по формуле:
, где
с = 0,04 h = 0,6
Слайд 19
Контроль:
→ расчёты проведены верно.
По данным таблицы находим условные моменты:
Находим числовые характеристики выборки:





























