- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Линии на плоскости
Содержание
- 2. План:Астроида Кардиоида Конхоида Никомеда Лемниската Бернулли Спираль Архимеда Улитка Паскаля Спираль Циклоида
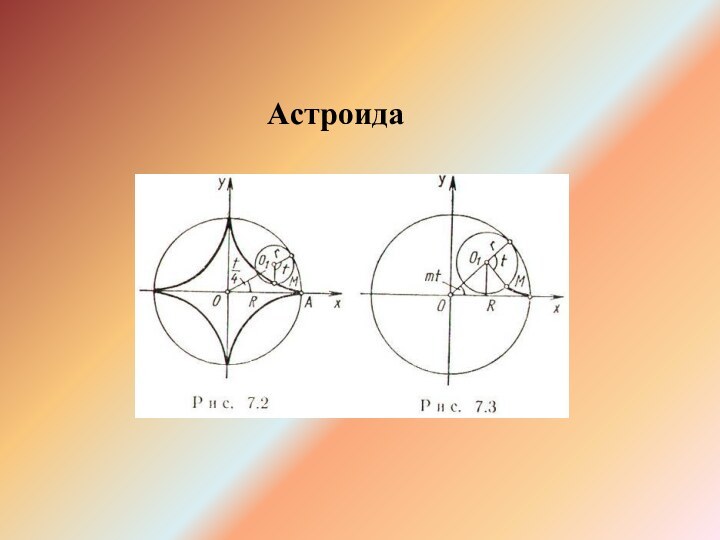
- 3. Астроида
- 4. Уравнение в декартовых координатах:
- 5. Уравнение в декартовых координатах:
- 6. Конхоида НикомедаКонхоида Никомеда - линия, полученная при
- 7. Конхоида Никомеда
- 8. Лемниската БернуллиУравнение в декартовых координатах:
- 9. Лемниската Бернулли
- 10. Спираль Архимеда Длина дуги между точками
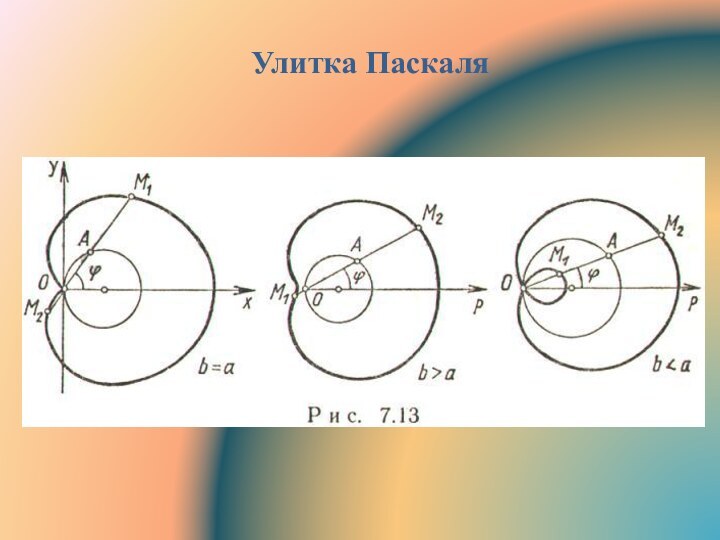
- 12. Улитка Паскаля
- 13. На произвольном луче OA от точки A
- 14. Циклоида - линия, которую описывает точка M,
- 15. Обыкновенная циклоида Параметрические уравнения:
- 16. Удлиненная (укороченная) циклоида Параметрические уравнения:x = at
- 17. Скачать презентацию
- 18. Похожие презентации
План:Астроида Кардиоида Конхоида Никомеда Лемниската Бернулли Спираль Архимеда Улитка Паскаля Спираль Циклоида












Слайд 4
Уравнение в декартовых координатах:
Параметрические
уравнения:
Площадь, ограниченная астроидой:
Длина дуги от точки A до произвольной точки M(t):Длина всей астроиды: s = 6R.
Радиус кривизны в произвольной точке:
Слайд 5
Уравнение в декартовых координатах:
Параметрические
уравнения:
Полярное уравнение (с полюсом в точке
A):Длина дуги от точки A до произвольной точки M:
Длина всей кардиоиды: s = 16r.
Площадь, ограниченная кардиоидой:
Радиус кривизны в произвольной точке:
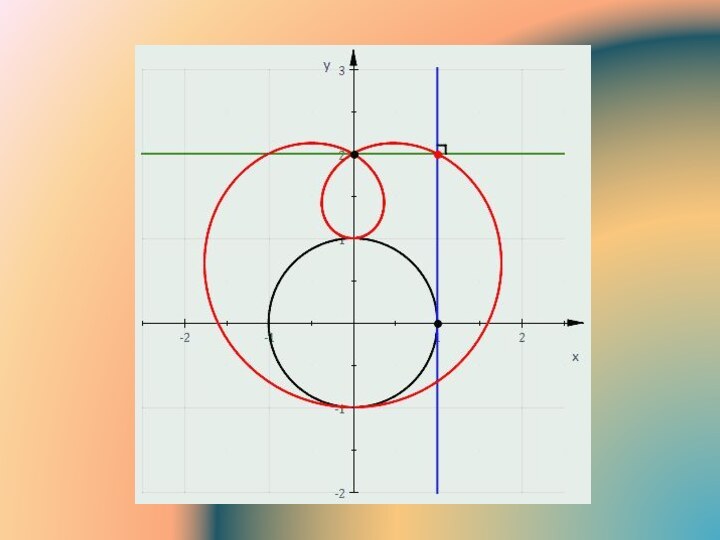
Кардиоида
Слайд 6
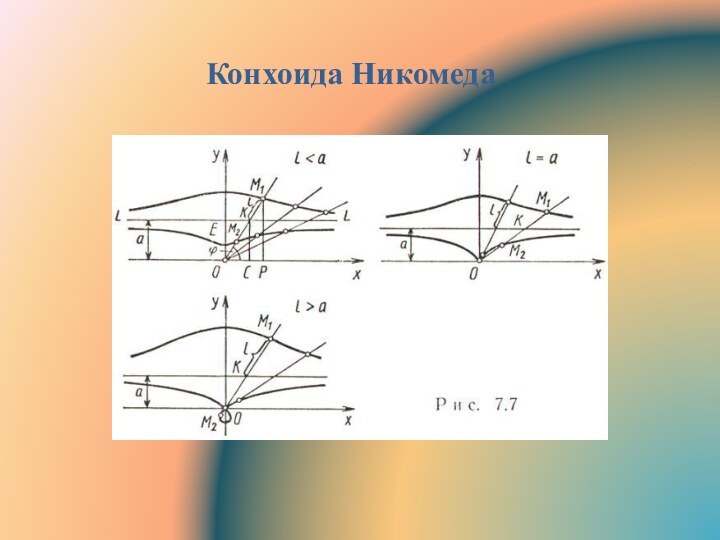
Конхоида Никомеда
Конхоида Никомеда - линия, полученная при увеличении
или уменьшении каждого радиуса-вектора точек данной прямой y =
a на одну и ту же величину l, т. е. Уравнение в декартовых координатах:
Полярное уравнение:
Асимптота: y = a.
Слайд 8
Лемниската Бернулли
Уравнение в декартовых координатах:
Полярное
уравнение:
Длина дуги лемнискаты между точками,
для которых и (эллиптический интервал первого рода).
Площадь сектора между осью и радиусом-вектором, соответствующим углу
Радиус кривизны:
Слайд 10
Спираль Архимеда
Длина дуги между точками
Площадь сектора, ограниченного дугой спирали Архимеда и двумя
радиусами-векторами и , соответствующими углам и :Площадь, ограниченная полярной осью и n-м витком спирали:
и
Слайд 13
На произвольном луче OA от точки A
пересечения
его с окружностью
по обе стороны откладываются отрезки
Улитка Паскаля - множество точек Мi.Уравнение в декартовых координатах:
Уравнение в полярных координатах:
Площадь, ограниченная улиткой (для случая l > 2a):
При l = 2a получается кардиоида.
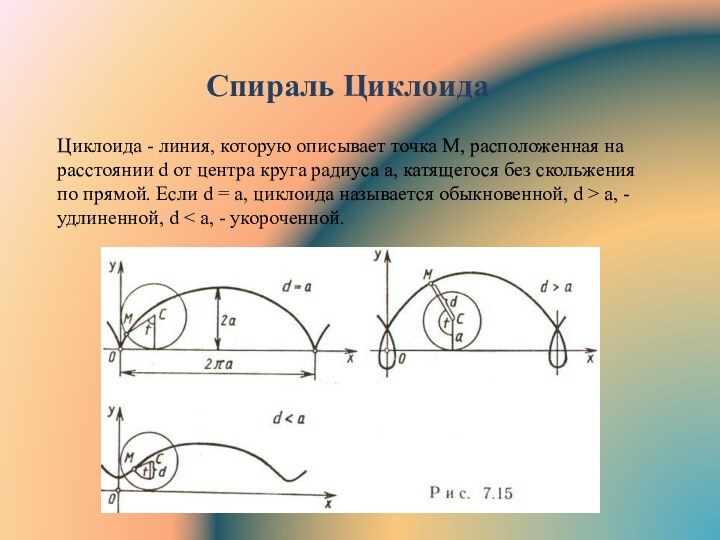
Слайд 14 Циклоида - линия, которую описывает точка M, расположенная
на расстоянии d от центра круга радиуса a, катящегося
без скольжения по прямой. Если d = a, циклоида называется обыкновенной, d > a, - удлиненной, d < a, - укороченной.Спираль Циклоида
Слайд 15
Обыкновенная циклоида
Параметрические уравнения:
Уравнение в декартовых координатах:
Длина дуги циклоиды
от исходной точки (t = 0) до произвольной точки M (t):Длина одной арки циклоиды: s = 8a.
Площадь, ограниченная одной аркой циклоиды и ее базисом:
Радиус кривизны в произвольной точке:
Слайд 16
Удлиненная (укороченная) циклоида
Параметрические уравнения:
x = at -
в sin t, y = a - в cos
t.Циссоида Диоклеса





























