Презентация на тему Машина Тьюринга

процесс, идущий от варьируемых исходных данных к искомому результату

(Марков А.А.)
Свойства алгоритма:
1) Дискретность.
2) Определенность.
3) Результативность.
4) Массовость.

математическая модель идеализированной цифровой вычислительной машины.
Устройство машины Тьюринга.
Лента.
Считывающая головка.
Устройство

управления.
Внутренняя память.

записан только один символ (буква) из внешнего алфавита A

= {˄, a1,a2,…,an-1}, 2≥n .

Пустая ячейка обозначается символом ˄, а сам символ ˄ называется пустым, при этом остальные символы называются непустыми.

записывать в нее новый символ из алфавита А. В

одном такте работы она может сдвигаться только на одну ячейку вправо (П), влево (Л) или оставаться на месте (Н).

конечное множество внутренних состояний Q = {q0, q1, …

, qm}, m≥ 1. Будем считать, что мощность | Q |≥2. Два состояния машины имеют особое значение: q1 – начальное внутреннее состояние (начальных внутренних состояний может быть несколько), q0 – заключительное состояние или стоп-состояние (заключительное состояние всегда одно). В каждый момент времени МТ характеризуется положением головки и внутренним состоянием.

момент t символ ai на новый символ aj (в

частности оставляет его без изменений, т. е. ai = aj );
Передвигает головку в одном из следующих направлений: Н, Л, П;
Изменяет имеющееся в момент t внутреннее состояние машины qi на новое qj , в котором будет машина в момент времени t +1. Такие действия устройства управления называют командой, которую можно записать в виде:

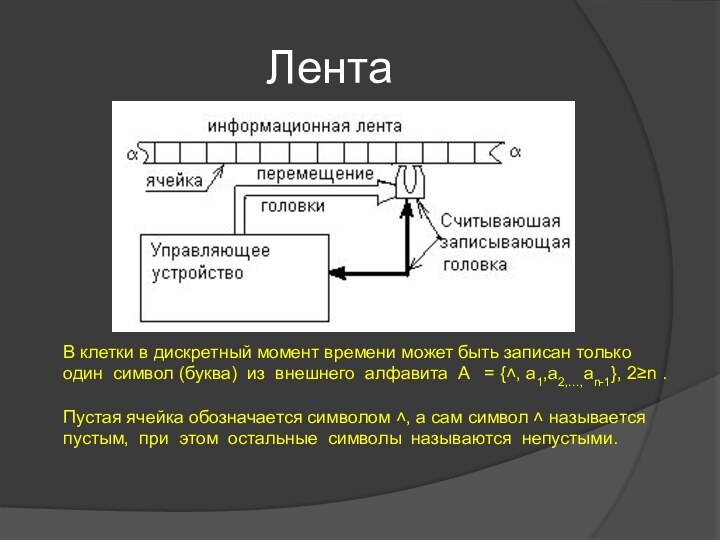
qiai ajDqj

первый (начальный) момент:
Слова на ленте, т. е. последовательности

символов, записанных в клетках ленты (слово получается чтением этих символов по клеткам ленты слева направо);
Положения головки;
Внутреннего состояния машины.

a1, a2, ˄, a1 , a1 то начальная конфигурация

будет иметь вид:

Работа машины Тьюринга состоит в последовательном применении команд, причем, применение той или команды определяется текущей конфигурацией. Так в приведенном выше примере должна применятся команда с левой частью q1a1 .

Результатом работы машины считается слово, которое будет записано на ленте в заключительной конфигурации, т. е. в конфигурации, в которой внутреннее состояние машины есть q0 .

, которая применима ко всем словам с внешним алфавитом

{a,b} и делает следующее: любое слово x1,x2…xn , где xi = a или xi = b (i = 1, 2 … n) преобразует в слово x2, …xn, x1 т. е., начиная работать при слове x1,x2…xn на ленте в начальной конфигурации, машина остановится, и в заключительной конфигурации на некотором участке ленты будет записано слово x2, …xn, x1, а все остальные клетки ленты (если такие будут) окажутся пустыми.

A={˄, a, b} , а за внутренний – Q

= {q0, q1, q2, q3}.

Команды определим следующим образом:

q1a ˄Пq2, q1b ˄Пq3, qiy ˄ППi , где yϵ{a, b}, i =2, 3;

q2˄ aHq0, q3˄ bHq0

Рассмотрим работу машины T1 над словом ba . В работе машины над
словом ba начальная конфигурация имеет следующий вид:

aПП3 и на машине создается конфигурация:

Наконец, третий шаг обусловлен

командой q3˄ bHq0. В результате чего создается конфигурация:

Эта конфигурация является заключительной, так как машина оказалась в состоянии остановки q0.
Таким образом, слово ba переработано в слово ab .

На первом шаге действует команда: q1b ˄Пq3 . В результате создается следующая конфигурация:

примера 1 к слову bbabb, исходя из начального положения,

при котором в состоянии q1 обозревается крайняя левая ячейка, в котором содержится символ этого слова.

Решение: