- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Метод Гаусса.
Содержание
- 2. Составим для нее расширенную матрицу, отделив столбец правых частей вертикальной чертой:знак равенства.правую часть уравнения;
- 3. Вспомним элементарные преобразования, не изменяющие решение системы.Для
- 4. Прямой ходПриведем расширенную матрицу системы Р к ступенчатому виду с помощью элементарных преобразований :Возможны двеситуации:
- 5. которое не имеет решений.Решение закончено, обратный ход
- 6. и система уравнений совместна.Выделим базисный минор и отбросим нулевые строки:
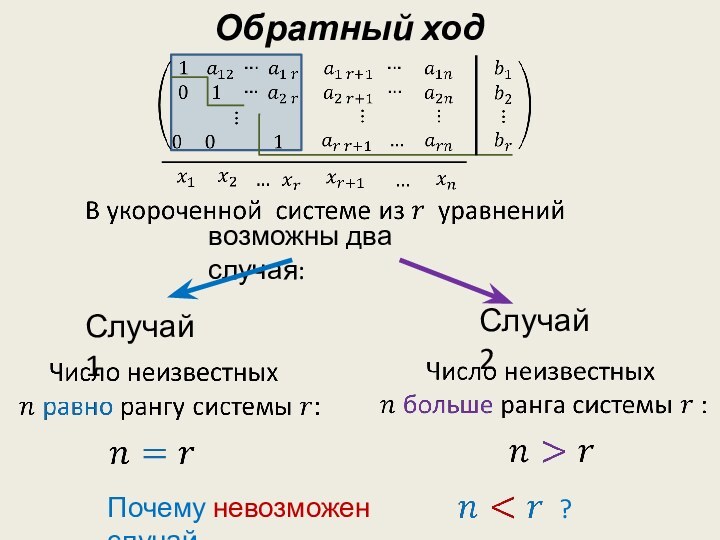
- 7. Обратный ходвозможны два случая:Случай 1Случай 2Почему невозможен случай?
- 8. Случай 1то есть матрица системы стала треугольной
- 9. Случай 2назовем их БАЗИСНЫМИ.ВОПРОС: сколько свободных неизвестных? БАЗИСНЫЕСВОБОДНЫЕ
- 10. Придадим свободным переменным любые значения и подставим их в уравнения:Перейдем от матричной формы записи к уравнениям:БАЗИСНЫЕСВОБОДНЫЕБАЗИСНЫЕСВОБОДНЫЕ
- 11. Выразим базисные переменные через свободные. Для этого
- 12. Пример 1Решить систему уравнений методом Гаусса:РЕШЕНИЕ:Прямой ходнесовместна.ОТВЕТ : нет решений.
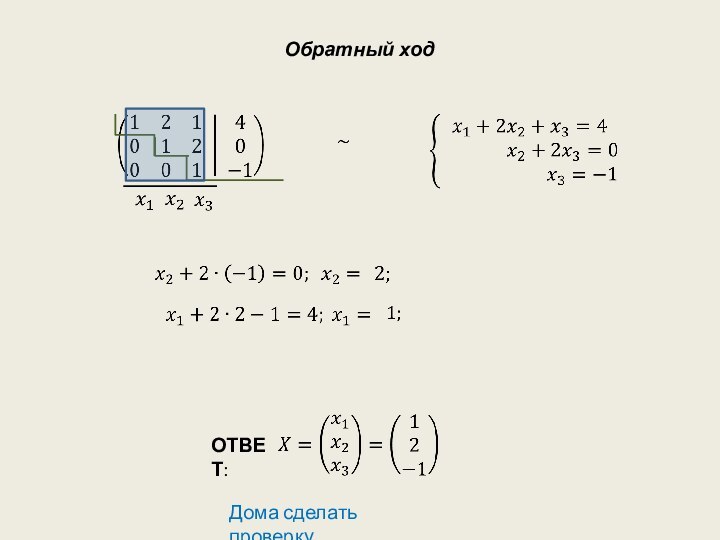
- 13. Пример 2Решить систему уравнений методом Гаусса:РЕШЕНИЕ:Прямой ходСистема совместна, случай 1.
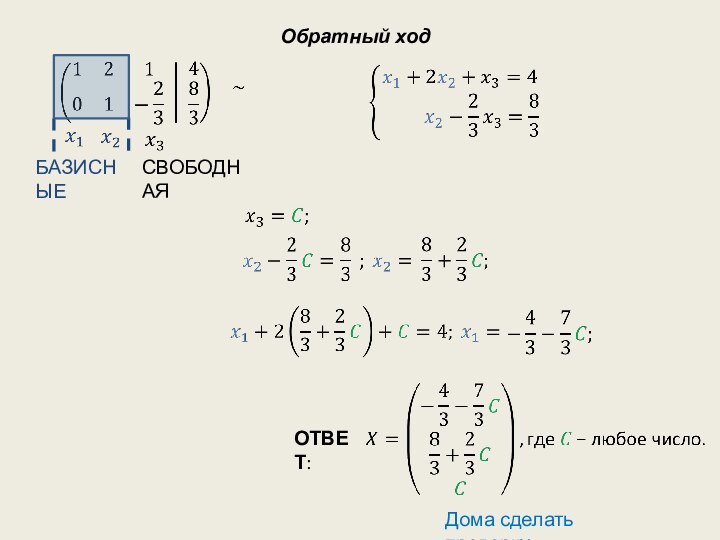
- 14. Обратный ходОТВЕТ: Дома сделать проверку.
- 15. Пример 3Решить систему уравнений методом Гаусса:РЕШЕНИЕ:Прямой ходСистема совместна, случай 2.
- 16. Скачать презентацию
- 17. Похожие презентации
Составим для нее расширенную матрицу, отделив столбец правых частей вертикальной чертой:знак равенства.правую часть уравнения;
Слайд 3
Вспомним элементарные преобразования, не изменяющие решение системы.
Для расширенной
матрицы системы Р допустимы:
Преобразования коэффициентов при неизвестных и правых
частей системы удобно выполнять в матричной форме.Метод Гаусса состоит в последовательном исключении неизвестных с помощью элементарных преобразований.
Вычисления проводятся в два этапа, называемых ПРЯМЫМ и ОБРАТНЫМ ХОДОМ.
ЗАМЕЧАНИЕ: рекомендуется нумеровать столбцы или проставлять под столбцами соответствующие неизвестные:
Слайд 4
Прямой ход
Приведем расширенную матрицу системы Р к ступенчатому
виду с помощью элементарных преобразований :
Возможны две
ситуации:
Слайд 5
которое не имеет решений.
Решение закончено, обратный ход метода
Гаусса не нужен.
система несовместна.
Какой ответ следует дать ?
Слайд 8
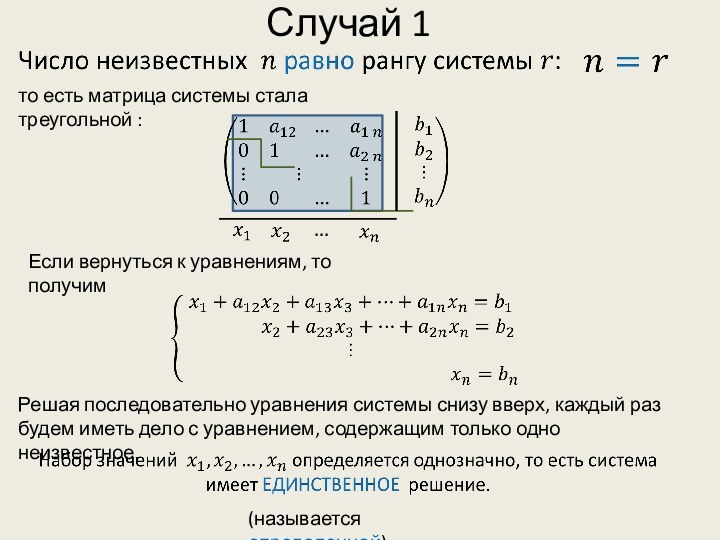
Случай 1
то есть матрица системы стала треугольной :
Если
вернуться к уравнениям, то получим
Решая последовательно уравнения системы снизу
вверх, каждый раз будем иметь дело с уравнением, содержащим только одно неизвестное.(называется определенной)
Слайд 10 Придадим свободным переменным любые значения и подставим их
в уравнения:
Перейдем от матричной формы записи к уравнениям:
БАЗИСНЫЕ
СВОБОДНЫЕ
БАЗИСНЫЕ
СВОБОДНЫЕ
Слайд 11 Выразим базисные переменные через свободные. Для этого перенесем
в правую часть уравнений слагаемые со свободными переменными
(изменив знак
на противоположный!!!):Придавая свободным переменным другие значения, получим другие значения базисных. Система будет иметь БЕСКОНЕЧНОЕ МНОЖЕСТВО решений.
БАЗИСНЫЕ
СВОБОДНЫЕ
Вычислим базисные переменные(как в случае 1), решая последовательно уравнения системы снизу вверх.
(называется неопределенной)
Слайд 12
Пример 1
Решить систему уравнений методом Гаусса:
РЕШЕНИЕ:
Прямой ход
несовместна.
ОТВЕТ :
нет решений.
Слайд 13
Пример 2
Решить систему уравнений методом Гаусса:
РЕШЕНИЕ:
Прямой ход
Система совместна,
случай 1.
Слайд 15
Пример 3
Решить систему уравнений методом Гаусса:
РЕШЕНИЕ:
Прямой ход
Система совместна,
