Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Метод математической индукции

Содержание

ИндукцияInductio (лат) - наведениеВид умозаключений, при котором на основании анализа частных суждений о принадлежности признака некоторым отдельным элементам множества делается вывод о принадлежности этого признака всему множеству
Метод математической индукцииЭлементы математической логикиТеория множеств ИндукцияInductio (лат) - наведениеВид умозаключений, при котором на основании анализа частных суждений Аксиомы Пеано1. Для каждого натурального числа а существует одно и только одно Аксиомы Пеано3. Ни одно натуральное число не следует за двумя различными натуральными Метод математической индукции1.База индукцииУтверждение проверяется для некоторого начального элемента, например n=1Даёт возможность Метод математической индукции2. Гипотеза индукцииФормулируется гипотеза о том, что утверждение справедливо для Метод математической индукции3. Шаг индукцииДоказывается, что если из справедливости утверждения для произвольного ПримерДоказать, что nN справедливо равенство 1. База индукцииПроверим равенство при n=1Следовательно, формула верна 2. Гипотеза индукцииДопустим, что равенство верно при некотором n=kN 3. Шаг индукцииДокажем, что если гипотеза верна, то равенство верно при 3. Шаг индукцииГипотеза 3. Шаг индукции 3. Шаг индукцииПолучили верное равенство.Формула справедлива для n=k+1 при условии её выполнимости ПримерДоказать, что nN 62n-1 кратно 35 1. База индукцииПроверим справедливость утверждения при n=1 62 - 1 = 36 2. Гипотеза индукцииПусть при n=k утверждение справедливо 62k – 1 делится без остатка на 35 3. Шаг индукцииДокажем справедливость утверждения при n=k+1 62(k+1) – 1 делится без 3. Шаг индукции36×62k – 1 = = 36×62k – 1 +36 – 3. Шаг индукции 36 (62k – 1) + 35 ГипотезаДелится на 35Делится на 35Делится на 35
Слайды презентации

Слайд 2 Индукция
Inductio (лат) - наведение

Вид умозаключений, при котором на

ИндукцияInductio (лат) - наведениеВид умозаключений, при котором на основании анализа частных

основании анализа частных суждений о принадлежности признака некоторым отдельным

элементам множества делается вывод о принадлежности этого признака всему множеству

Слайд 3 Аксиомы Пеано
1. Для каждого натурального числа а существует

Аксиомы Пеано1. Для каждого натурального числа а существует одно и только

одно и только одно следующее за ним число а’

2.

Единица является натуральным числом, причём она не следует ни за каким натуральным числом

Слайд 4 Аксиомы Пеано
3. Ни одно натуральное число не следует

Аксиомы Пеано3. Ни одно натуральное число не следует за двумя различными

за двумя различными натуральными числами.

4. Если множество А содержит

единицу и вместе с каждым числом а содержит следующее за ним число а’, то А содержит все натуральные числа.

Слайд 5 Метод математической индукции
1.База индукции
Утверждение проверяется для некоторого начального

Метод математической индукции1.База индукцииУтверждение проверяется для некоторого начального элемента, например n=1Даёт

элемента, например n=1

Даёт возможность определить нижнюю границу применения формулы

или действия неравенства.

Слайд 6 Метод математической индукции
2. Гипотеза индукции
Формулируется гипотеза о том,

Метод математической индукции2. Гипотеза индукцииФормулируется гипотеза о том, что утверждение справедливо

что утверждение справедливо для некоторого kN

Шаг к обобщению, который

формулируется в виде гипотезы. Это индуктивная фаза: от одного частного случая перешли к обобщению.

Слайд 7 Метод математической индукции
3. Шаг индукции
Доказывается, что
если из

Метод математической индукции3. Шаг индукцииДоказывается, что если из справедливости утверждения для

справедливости утверждения для произвольного n=kN следует, что

оно справедливо для n=k+1,
то данное утверждение справедливо и для любого натурального числа n

Фаза доказательства. Устанавливаем, насколько сильны индуктивные выводы.

Слайд 8 Пример
Доказать, что nN справедливо равенство

ПримерДоказать, что nN справедливо равенство

Слайд 9 1. База индукции
Проверим равенство при n=1





Следовательно, формула верна



1. База индукцииПроверим равенство при n=1Следовательно, формула верна

Слайд 10 2. Гипотеза индукции
Допустим, что равенство верно при некотором

2. Гипотеза индукцииДопустим, что равенство верно при некотором n=kN

n=kN








Слайд 11 3. Шаг индукции
Докажем, что если гипотеза верна, то

3. Шаг индукцииДокажем, что если гипотеза верна, то равенство верно при некотором n=k+1, то есть

равенство верно при некотором n=k+1, то есть








Слайд 12 3. Шаг индукции
Гипотеза

3. Шаг индукцииГипотеза

Слайд 13 3. Шаг индукции

3. Шаг индукции

Слайд 14 3. Шаг индукции
Получили верное равенство.

Формула справедлива для n=k+1

3. Шаг индукцииПолучили верное равенство.Формула справедлива для n=k+1 при условии её

при условии её выполнимости при n=k.

 она справедлива 

nN

Слайд 15 Пример
Доказать, что nN

62n-1

ПримерДоказать, что nN 62n-1 кратно 35

кратно 35




Слайд 16 1. База индукции
Проверим справедливость утверждения при n=1

62

1. База индукцииПроверим справедливость утверждения при n=1 62 - 1 =

- 1 = 36 -1 = 35

35 делится без

остатка на 35
Следовательно, утверждение верно.




Слайд 17 2. Гипотеза индукции
Пусть при n=k утверждение справедливо

62k

2. Гипотеза индукцииПусть при n=k утверждение справедливо 62k – 1 делится без остатка на 35

– 1 делится без остатка на 35





Слайд 18 3. Шаг индукции
Докажем справедливость утверждения при n=k+1

62(k+1)

3. Шаг индукцииДокажем справедливость утверждения при n=k+1 62(k+1) – 1 делится

– 1 делится без остатка на 35

62(k+1) – 1

= 62k+2 – 1=
= 62k×62 – 1 =36×62k – 1




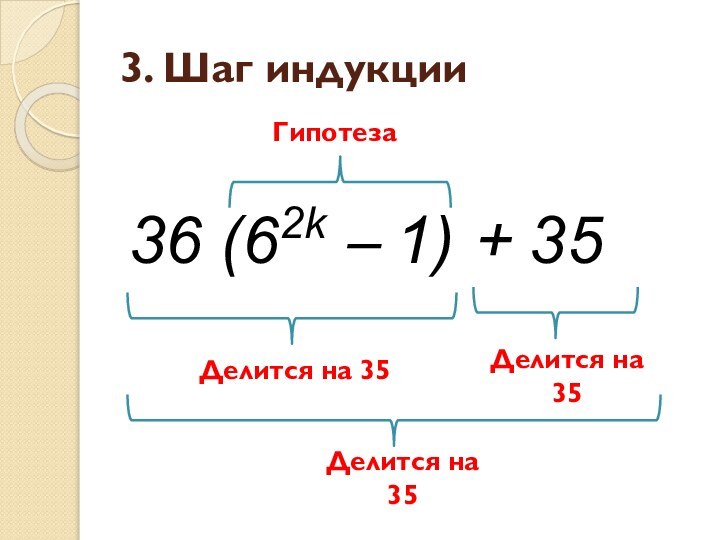
Слайд 19 3. Шаг индукции
36×62k – 1 =
= 36×62k

3. Шаг индукции36×62k – 1 = = 36×62k – 1 +36

– 1 +36 – 36 =
= 36×62k – 36

+ 35 =
= 36 (62k – 1) + 35




  • Имя файла: metod-matematicheskoy-induktsii.pptx
  • Количество просмотров: 102
  • Количество скачиваний: 0
- Предыдущая Как питаться правильно?
Следующая - Урбанизация: процессы и тенденция

Похожие презентации

презентация Я такой же как ты! познавательное развитие детей старшего дошкольного возраста презентация урока для интерактивной доски (старшая группа) презентация Я такой же как ты! познавательное развитие детей старшего дошкольного возраста презентация урока для интерактивной доски (старшая группа) 162
Презентация по окружающему миру Животные и растения Красной книги России 2 класс . Презентация по окружающему миру Животные и растения Красной книги России 2 класс . 123
МОЁ ПОРТФОЛИО. презентация МОЁ ПОРТФОЛИО. презентация 119
Презентация к родительскому собранию Наши трудные дети презентация к уроку Презентация к родительскому собранию Наши трудные дети презентация к уроку 147
Мониторинг результативности деятельности педагога в межаттестационный период Мониторинг результативности деятельности педагога в межаттестационный период 102
Клеточная инженерия Клеточная инженерия 144
Шаблон презентации Шаблон презентации 78
Coca-Cola.Вред или польза? проект (2 класс) Coca-Cola.Вред или польза? проект (2 класс) 155
Наш мобильный робот Наш мобильный робот 172
fizkultminutka fizkultminutka 136
Поисковые системы Поисковые системы 94
презентация Играем в театр презентация к занятию (старшая группа) по теме презентация Играем в театр презентация к занятию (старшая группа) по теме 96
Презентация по татарскому языку на тему Имя существительное (3 класс) Презентация по татарскому языку на тему Имя существительное (3 класс) 116
Презентация Физкультурно - оздоровительная работа в группе №4 Звёздочки Презентация Физкультурно - оздоровительная работа в группе №4 Звёздочки 90
Порядок заповнення податкової декларації платника єдиного податку Порядок заповнення податкової декларації платника єдиного податку 88
Дегазация Земли и проблема безопасности угледобычи в Кузбассе Дегазация Земли и проблема безопасности угледобычи в Кузбассе 102
блокада презентация занятия для интерактивной доски (подготовительная группа) блокада презентация занятия для интерактивной доски (подготовительная группа) 109
Убеждай и побеждай! Убеждай и побеждай! 125
Шаблон для создания презентаций Тетрадь на спирали презентация к уроку (1, 2, 3, 4 класс) Шаблон для создания презентаций Тетрадь на спирали презентация к уроку (1, 2, 3, 4 класс) 101
Вегетативное размножение растения Вегетативное размножение растения 89
umk perspektivnaya nachalnaya shkola umk perspektivnaya nachalnaya shkola 88
prezentatsiya3 prezentatsiya3 79
Пейзаж - поэтическая и музыкальная живопись презентация к уроку Пейзаж - поэтическая и музыкальная живопись презентация к уроку 126
Проект Чистота - залог здоровья. консультация (старшая группа) Проект Чистота - залог здоровья. консультация (старшая группа) 144
Лэпбук Театр в жизни дошкольника. презентация к уроку (младшая, средняя, старшая, подготовительная группа) Лэпбук Театр в жизни дошкольника. презентация к уроку (младшая, средняя, старшая, подготовительная группа) 90
kopiya portfolio 3a kopiya portfolio 3a 150
НЕМНОГО О МОТИВАХ И ЦЕЛЯХ ВСТУПЛЕНИЯ В КОММУНИКАЦИЮ НЕМНОГО О МОТИВАХ И ЦЕЛЯХ ВСТУПЛЕНИЯ В КОММУНИКАЦИЮ 100
Петропавловский собор Петропавловский собор 118
Презентация по татарскому языку на тему: Ашамлыклар(3класс) Презентация по татарскому языку на тему: Ашамлыклар(3класс) 112
ПК 4.3.Технологии обучения статья (3 класс) по теме ПК 4.3.Технологии обучения статья (3 класс) по теме 40