Презентация на тему Метод Ньютона-Рафсона

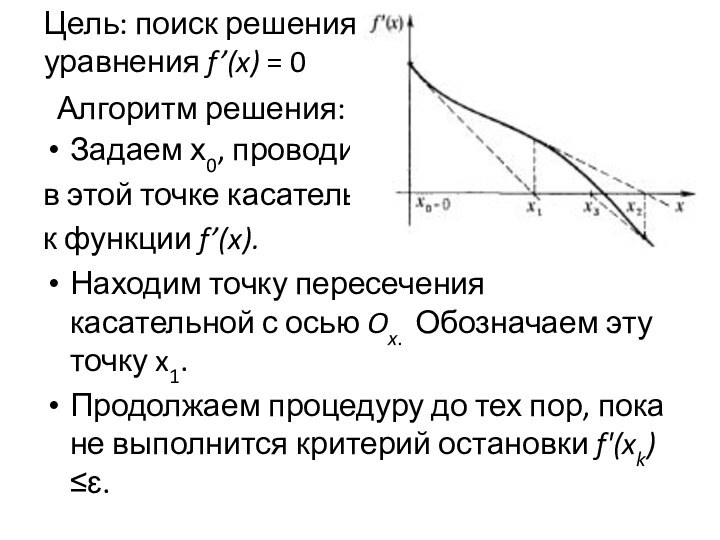
к функции f’(x).
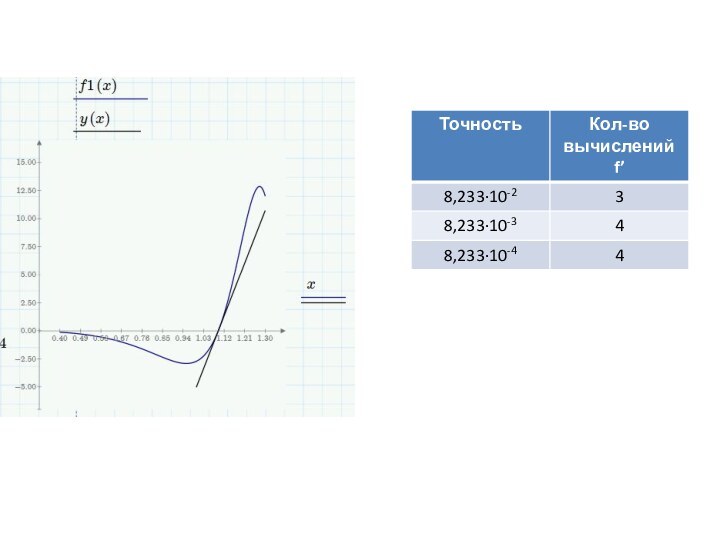
Находим точку пересечения касательной с осью Ox.

Обозначаем эту точку x1.
Продолжаем процедуру до тех пор, пока не выполнится критерий остановки f'(xk)≤ԑ.

Цель: поиск решения уравнения f’(x) = 0

это выражение к нулю,
найдем xk+1
xk+1 = xk - (f’(xk)/

f’(xk))

минимума для производной с погрешностью ԑ = 1,3·10-2.
Имеем


1. f’(x0)

= -0,439, Ӏf’Ӏ≥ԑ, поэтому продолжаем вычисления
f’’ = 0,12, x1 = 1- (-0,439/0.12) = 4,658.
2. f’(x1) = 0,344, Ӏf’Ӏ≥ԑ, продолжаем вычисления
f’’ = 0.182, x2 = 2,786.
3. f’(x2) = -0,093, Ӏf’Ӏ≥ԑ, продолжаем вычисления
f’’ = 0,246, x3 = 2,786- (-0,093/0.246) = 3,146.
4. f’(x3) = 0,0011, Ӏf’Ӏ≤ԑ.

минимума для производной с погрешностью ԑ=8,233·10-2.

1. f’(1,2) = 8.233,

Ӏ f’(1,25)Ӏ ≥ ԑ.
f’’(1,25) = 92,779
x1 = 1,2 - (8,233)/(92,779) = 1,111
2. f’(1,111) =0,926, Ӏ f’(1,017)Ӏ ≥ ԑ
f’’(1,017) = 60,934
x2 = 1,0958
3. f’(1,0958) = 0,0664, Ӏ f’(1,176)Ӏ ≤ ԑ