Слайд 2
Множеством называется неупорядоченный ограниченный набор однотипных данных.
Все
элементы множества должны принадлежать одному из скалярных (простых) типов,
кроме вещественных. Этот тип называется базовым типом множества. Базовый тип задается перечислением или диапазоном значений.
Если множество не имеет элементов, оно называется пустым и обозначается как [ ] .
Слайд 3
Количество элементов множества называется его мощностью (максимальное количество
255).
В множестве не может быть повторяющихся элементов.
Область
значений типа множество – набор всевозможных подмножеств, составленных из элементов базового типа.
Слайд 4
Способы описания множеств
1. Var имя множества : set
of тип элементов;
2. Type имя типа = set of
тип элементов;
Var имя множества : имя типа;
где,
set of - служебные слова ( множество из);
тип элементов – любой порядковый.
Слайд 5
Например:
Type mn = set of char;
Var
a,b: mn;
c: set of
2..6;
Begin
a:=[ ‘A’..’Z’];
c:=[2, 4..6];
b:=[];
. . .
End.
Слайд 6
Операции над множествами
1. Операция IN - используется для
проверки принадлежности какого-либо значения указанному множеству.
Обычно применяется в
операторах условного перехода . Результат выполнения операции логического типа ( True или False).
Слайд 7
Var s:char;
m1, m2: set
of char;
Begin
m1:=[‘0’..’9’];
m2:=[‘A’..’я’];
readln(s);
If s in m1 then writeln (‘цифра’)
else
if s in m2 then writeln (‘буква’);
. . .
end.
Пример:
Слайд 8
Операции над множествами
2. Объединение множеств (+) . Объединением
двух множеств является третье множество, содержащее элементы обоих множеств.
A:=[3,5,7..10,
15..20]
B:=[1..4, 6, 10..12]
C:=A+B
{ C:=[1..12, 15..20] }
Слайд 9
Операции над множествами
3. Пересечение множеств (*). Пересечением двух
множеств является третье множество, которое содержит элементы, входящие одновременно
в оба множества.
A:=[3,5,7..10, 15..20]
B:=[1..4, 6, 10..12]
C:=A*B { C:=[3,10] }
Слайд 10
Операции над множествами
4 Разность множеств (-). Разностью двух
множеств является третье множество, которое содержит элементы первого множества,
не входящие во второе множество.
A:=[3,5,7..10, 15..20]
B:=[1..4, 6, 10..12]
C:=A-B { C:=[5,7..9,15..20] }
Слайд 11
Операции над множествами
5. Операция «равно» (=). Два множества
А и В считаются равными, если они состоят из
одних и тех же элементов. Порядок следования элементов в сравниваемых множествах значения не имеет.
A:=[1,2,3]
B:=[3,2,1]
A=B {true}
Слайд 12
Операции над множествами
6. Операция «не равно» (). Два
множества А и В считаются не равными, если они
отличаются по мощности или по значению хотя бы одного элемента.
7. Операция «больше или равно» (>=) . Результат операции А>=B равен True , если все элементы множества В содержатся в множестве А.
8. Операция «меньше или равно» ( <=). Если все элементы множества А содержатся в множестве В , то результат равен True.
Слайд 14
Ввод элементов множества
Элементам множества задаются значения оператором присваивания.
Пример:
Var zn: set of char;
Begin
zn:=[‘;’, ‘.’, ‘?’, ‘
‘, ‘!’, ‘:’, ‘-’]; {знаки препинания}
. . .
End.
Слайд 15
Стандартные процедуры работы с множествами
Слайд 16
Вывод элементов множества
Program VivodMN;
Type mn=set of char;
Var
a:mn;
x: char;
begin
a:=[‘f’, ‘j’, ‘e’];
For x:=’a’ to ‘z’
do
If x in a then write (x);
End.
выход
Слайд 17
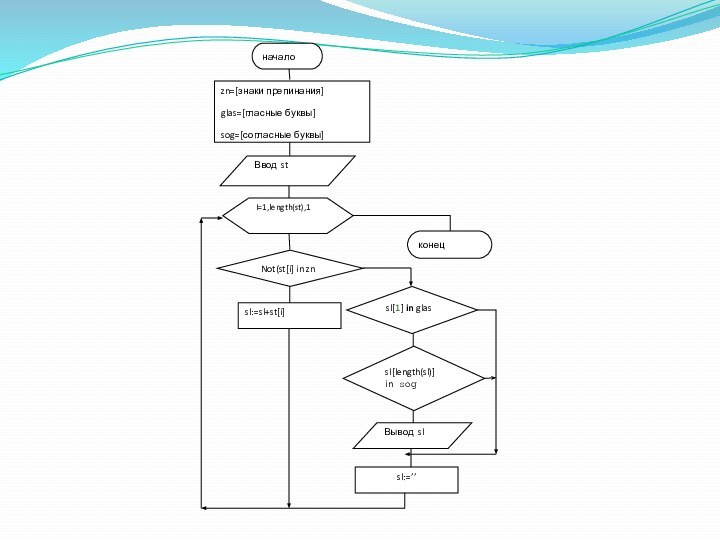
Пример 1:
Дана строка символов из строчных русских
букв , слова разделены любым знаком препинания . Вывести
слова начинающиеся с гласной буквы , а оканчивающиеся - согласной.
Слайд 19
program Mnog;
const
zn=[',','.',':',';','?','!',' '];
glas=['а','е','и','о','у','ю','я','э','ы','ё'];
sog=['б','в','г','д','ж','з','й','к','л','м','н','п','р','с','т','ф','х','ц','ч','ш','щ'];
var
St,sl:string;
i:integer;
begin
Writeln('Введите cтроку');
readln(st);
For i:=1 to length(st)
do
If not(st[i] in zn) then
sl:=sl+st[i] else
begin
if (sl[1] in
glas) and
(sl[length(sl)] in sog) then Writeln(sl);
sl:='';
end;
end.






![Множество Var s:char; m1, m2: set of char;Begin m1:=[‘0’..’9’]; m2:=[‘A’..’я’]; readln(s); If s in](/img/tmb/14/1338176/8f5faa165caae3eac86c6525ba2cb050-720x.jpg)










![Множество program Mnog;constzn=[',','.',':',';','?','!',' '];glas=['а','е','и','о','у','ю','я','э','ы','ё'];sog=['б','в','г','д','ж','з','й','к','л','м','н','п','р','с','т','ф','х','ц','ч','ш','щ'];var St,sl:string;i:integer;beginWriteln('Введите cтроку');readln(st);For i:=1 to length(st) doIf not(st[i] in zn)](/img/tmb/14/1338176/c3b90688c28c682f7c32e11f0cd34869-720x.jpg)






























