- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Непрерывная случайная величина. Числовые характеристики. Законы распределения.
Содержание
- 2. Определение случайной величиныСлучайная величина — это величина, которая
- 3. Непрерывная случайная величинаНепрерывной случайной величиной называется такая величина,
- 4. Плотность вероятностиПлотность вероятности непрерывной случайной величины, она же дифференциальная
- 5. Свойства плотности вероятностиЗначения функции неотрицательны, т.е. f(x)≥0Основное
- 6. Математическое ожиданиеДля непрерывной случайной величины, заданной функцией плотности
- 7. ПримерОпределим математическое ожидание случайной величины распределённой по закону Пуассона.
- 8. Дисперсия и среднеквадратичное отклонениеНазванные числовые характеристики дают представление о разбросе случайных величин относительно их среднего значения.
- 9. ДисперсияДисперсией (рассеянием) случайной величины называется математическое ожидание квадрата
- 10. Среднеквадратичное отклонениеСреднеквадратичным отклонением называют величину, равную корню
- 11. Равномерное распределениеНепрерывная величина Х распределена равномерно на интервале (a, b),
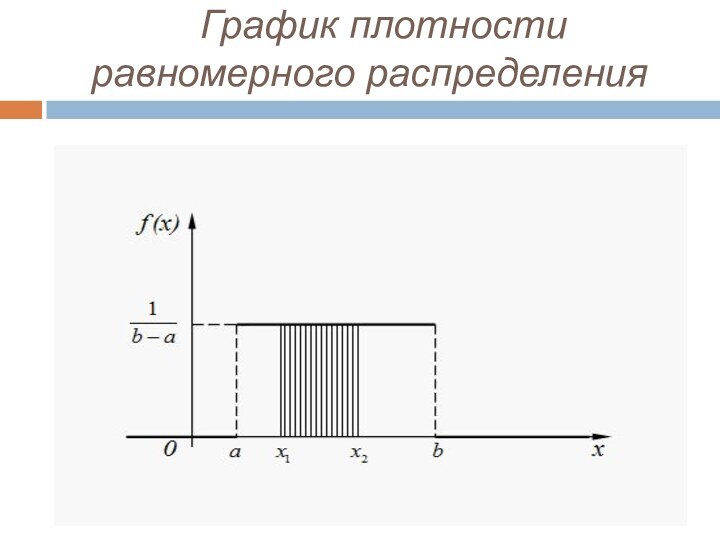
- 12. График плотности равномерного распределения
- 13. Показательное распределениеНепрерывная случайная величина Х имеет показательное распределение, если плотность распределения ее вероятностей выражается формулой:
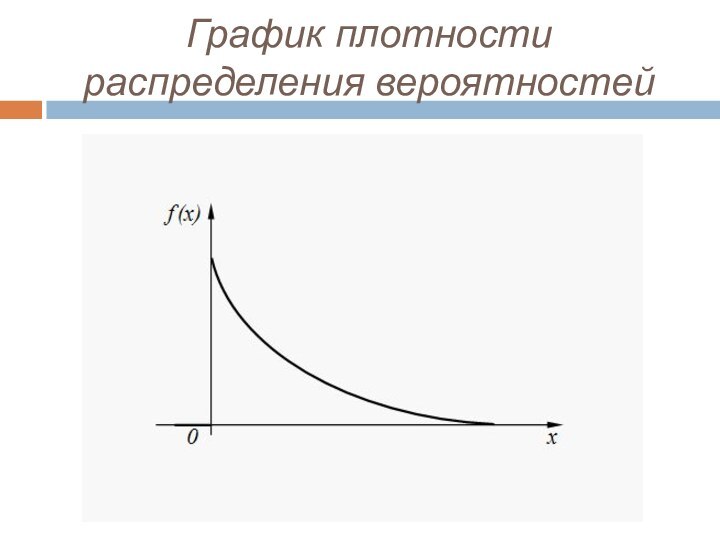
- 14. График плотности распределения вероятностей
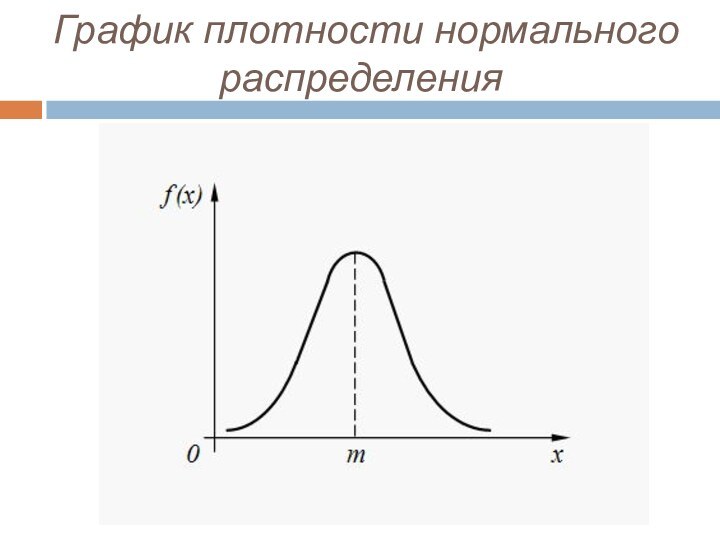
- 15. Нормальное (гауссово) распределениеСлучайная величина имеет нормальное (гауссово) распределение, если
- 16. Скачать презентацию
- 17. Похожие презентации
Определение случайной величиныСлучайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.













Слайд 3
Непрерывная случайная величина
Непрерывной случайной величиной называется такая величина, которая
может принимать любые значения из некоторого конечного или бесконечного
промежутка.Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
Слайд 4
Плотность вероятности
Плотность вероятности непрерывной случайной величины, она же дифференциальная функция
распределения вероятностей - аналог закона распределения дискретной случайной величины.
Плотность вероятностей
графически представляет собой непрерывную гладкую линию (или кусочно-гладкую, если на разных отрезках задаётся разными функциями). Для непрерывных случайных величин можно найти только вероятность попадания в какой-либо интервал. Считается, что для каждого отдельного (одиночного) значения непрерывной случайной величины вероятность равна нулю. И графически вероятность попадания в интервал выражается площадью фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом.
Слайд 5
Свойства плотности вероятности
Значения функции неотрицательны, т.е. f(x)≥0
Основное свойство
плотности вероятности: несобственный интеграл от плотности вероятности в пределах от
-∞ до +∞ равен единице (геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1).
Слайд 6
Математическое ожидание
Для непрерывной случайной величины, заданной функцией плотности вероятности f(x),
математическое ожидание определяется в виде интеграла
при условии, что
этот интеграл существует (если интеграл расходится, то говорят, что математическое ожидание не существует).
Слайд 7
Пример
Определим математическое ожидание случайной величины распределённой по закону Пуассона. По
определению
или обозначим
Значит, параметр, определяющий закон распределения пуассоновской случайной
величины равен среднему значению этой величины.
Слайд 8
Дисперсия и среднеквадратичное отклонение
Названные числовые характеристики дают представление
о разбросе случайных величин относительно их среднего значения.
Слайд 9
Дисперсия
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения
случайной величины от ее математического ожидания.
Свойство 1. Дисперсия постоянной
равна нулю. По определению:
Свойство 2. Постоянную можно выносить за знак дисперсии с возведением в квадрат.
Слайд 10
Среднеквадратичное отклонение
Среднеквадратичным отклонением называют величину, равную корню квадратному
из дисперсии.
Среднеквадратичное отклонение имеет ту же размерность, что и
сама случайная величина.
Слайд 11
Равномерное распределение
Непрерывная величина Х распределена равномерно на интервале (a, b), если
все ее возможные значения находятся на этом интервале и
плотность распределения вероятностей постоянна:Для случайной величины Х , равномерно распределенной в интервале (a, b) (рис. 4), вероятность попадания в любой интервал (x1, x2), лежащий внутри интервала (a, b), равна:
Слайд 13
Показательное распределение
Непрерывная случайная величина Х имеет показательное распределение,
если плотность распределения ее вероятностей выражается формулой:
Слайд 15
Нормальное (гауссово) распределение
Случайная величина имеет нормальное (гауссово) распределение, если плотность
распределения ее вероятностей определяется зависимостью:
где
,При нормальное распределение называется стандартным.





























