- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Подготовилиученицы vi класса АКазанцева Анастасия, Болдырева Юлия,Рюмина Елена.
Содержание
- 2. Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали.
- 3. История Кардиоида впервые встречается в трудах французского
- 4. Множество МандельбротаВизуально, внутри множества Мандельброта можно выделить
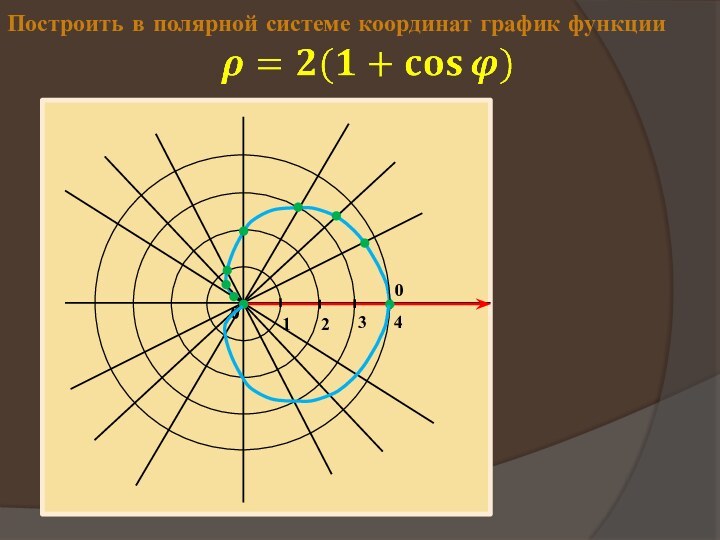
- 5. Построить в полярной системе координат график функции123400
- 6. Кардиоида (от греческих слов сердце и вид)
- 7. Кардиоиду можно построить и другим способом. Она
- 9. Скачать презентацию
- 10. Похожие презентации
Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали.







Слайд 3
История
Кардиоида впервые встречается в трудах французского учёного Луи
Карре. Название кривой дал Джованни Сальвемини ди Кастиллоне в
1741 г.«Спрямление», то есть вычисление длины кривой, выполнил Ла Ир, который открыл кривую независимо, в 1708 г. Также независимо описал кардиоиду голландский математик Й. Коерсма. В дальнейшем к кривой проявляли интерес многие видные математики XVIII-XIX веков.
Слайд 4
Множество Мандельброта
Визуально, внутри множества Мандельброта можно выделить бесконечное
количество элементарных фигур, причём самая большая в центре представляет
собой кардиоиду. Также есть набор кругов, касающихся кардиоиды, размер которых постепенно уменьшается, стремясь к нулю. Каждый из этих кругов имеет свой набор меньших кругов, диаметр которых также стремится к нулю и т. д. Этот процесс продолжается бесконечно, образуя фрактал. Также важно, что эти процессы ветвления фигур не исчерпывают полностью множество Мандельброта: если рассмотреть с увеличением дополнительные «ветки», то в них можно увидеть свои кардиоиды и круги, не связанные с главной фигурой.Слайд 6 Кардиоида (от греческих слов сердце и вид) –
получила свое название из-за схожести своих очертаний со стилизованным
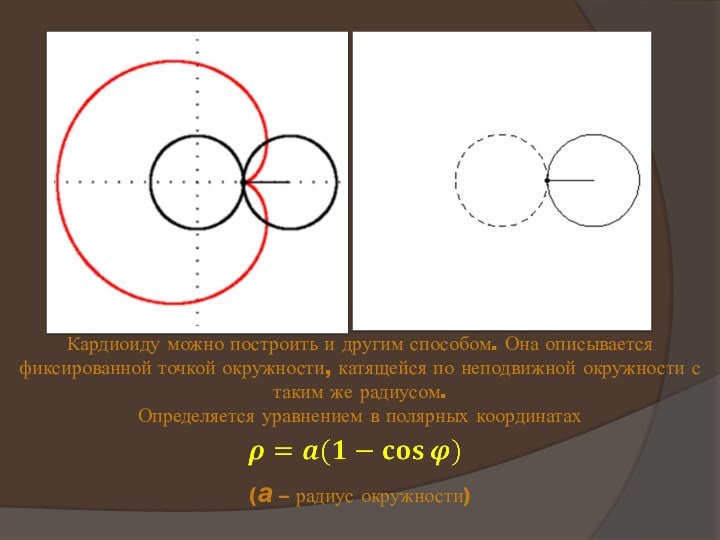
изображением сердца.Слайд 7 Кардиоиду можно построить и другим способом. Она описывается
фиксированной точкой окружности, катящейся по неподвижной окружности с таким
же радиусом.Определяется уравнением в полярных координатах
(а – радиус окружности)





























