- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Полуправильные многогранники
Содержание
- 2. Полуправильный многогранник - это выпуклый многогранник, гранями
- 3. К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых равны, а также антипризмы.
- 4. Архимедовы тела — выпуклые многогранники, все грани которых
- 5. Многогранник, двойственный (или дуальный) к заданному многограннику
- 6. Каталановы тела – выпуклые многогранники, имеющие одинаковые
- 7. Архимедовы тела являются полуправильными многогранниками в том
- 8. Существует 13 архимедовых тел, два из которых
- 9. Кубооктаэдр (8 треугольников, 6 квадратов)Ромбододекаэдр(12 ромбов)
- 10. (20 треугольников,
- 11. (4 треугольника,
- 12. (6 квадратов,
- 13. (12 пятиугольников, 20 шестиугольников) Усеченный икосаэдрПентакисдодэкаэдр (60 равнобедренных треугольников)
- 14. (6 восьмиугольников 8 треугольников)
- 15. (20 треугольников, 12 десятиугольников)
- 16. (18 квадратов, 8 треугольников)
- 18. (12
- 19. (30
- 20. (6 квадратов,
- 21. Скачать презентацию
- 22. Похожие презентации
Полуправильный многогранник - это выпуклый многогранник, гранями которого являются правильные многоугольники (возможно, и с разным числом сторон), и все многогранные углы равны.


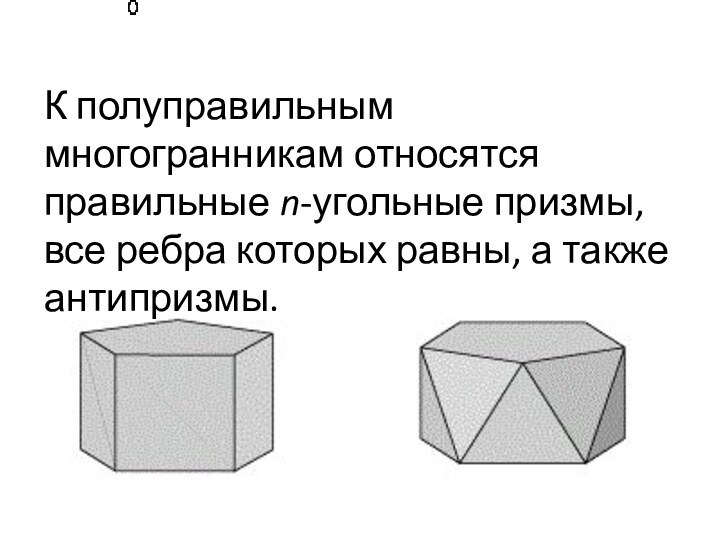
















Слайд 3 К полуправильным многогранникам относятся правильные n-угольные призмы, все
ребра которых равны, а также антипризмы.
Слайд 4 Архимедовы тела — выпуклые многогранники, все грани которых являются
правильными многоугольниками двух или более типов, для любой пары
вершин существует симметрия многогранника и все многогранные углы при вершинах конгруэнтны.Архимедовы тела
Слайд 5 Многогранник, двойственный (или дуальный) к заданному многограннику —
многогранник, у которого каждой грани исходного многогранника соответствует вершина
двойственного, каждой вершине исходного — грань двойственного и каждому ребру исходного — ребро двойственного. То есть, чтобы построить каталаново тело, необходимо взять архимедово тело и поменять все грани на вершины, объединить эти вершины в многоугольники, так чтобы было соответствие - вершина исходного - новая грань.Каталановы тела - многогранники, двойственные архимедовым телам.
Слайд 6 Каталановы тела – выпуклые многогранники, имеющие одинаковые конгруэнтные
грани, равные двугранные углы и правильные многогранные углы.
Каталановы тела
Слайд 7 Архимедовы тела являются полуправильными многогранниками в том смысле,
что их грани — правильные многоугольники, но они не одинаковы,
а каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.Отличие архимедовых тел от каталановых
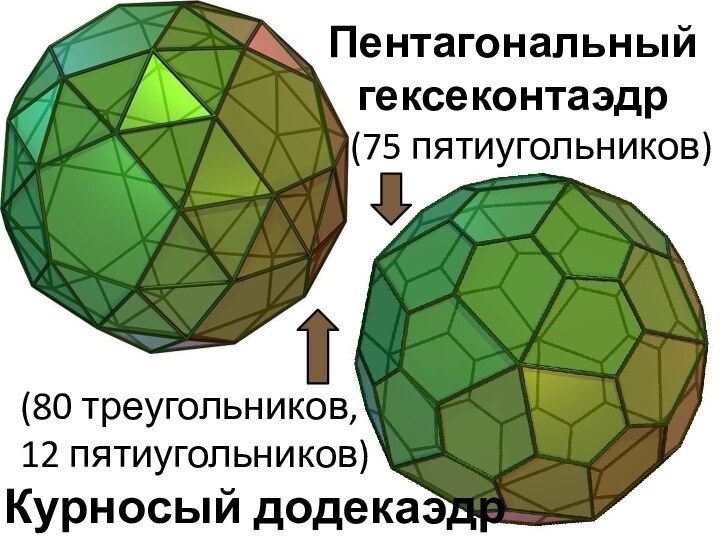
Слайд 8 Существует 13 архимедовых тел, два из которых (курносый
куб и курносый додекаэдр) не являются зеркально-симметричными и имеют
левую и правую формы. Соответственно, существует 13 каталановых тел.Полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Соответственно, существует 26 полуправильных многогранников, не считая правильной призмы и антипризмы.
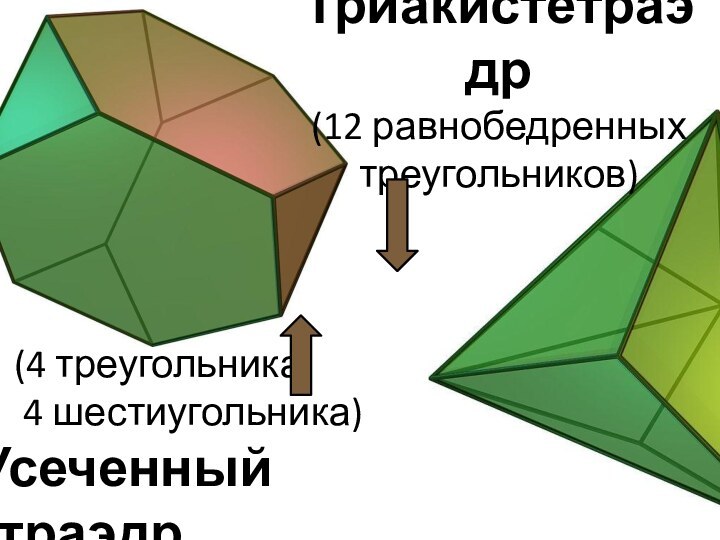
Слайд 11 (4 треугольника,
4 шестиугольника)
Усеченный тетраэдр
Триакистетраэдр
(12 равнобедренных треугольников)
Слайд 12
(6 квадратов,
8 шестиугольников)
Усеченный октаэдр
Тетракисгексаэдр
(24 равнобедренных
треугольника)
Слайд 13
(12 пятиугольников,
20 шестиугольников)
Усеченный икосаэдр
Пентакисдодэкаэдр
(60 равнобедренных треугольников)
Слайд 14
(6 восьмиугольников
8 треугольников)
Усеченный
куб
Триакисоктаэдр
(24 равнобедренных
треугольника)
Слайд 15
(20 треугольников,
12 десятиугольников)
Усеченный
додекаэдр
Триакисикосаэдр
(60 равнобедренных
треугольников)
Слайд 16
(18 квадратов,
8 треугольников)
Ромбокубооктаэдр
Дельтоидальный икоситетраэдр
(24 выпуклых дельтоида)Слайд 17 (20
треугольников,
30 квадратов, 12 пятиугольников) РомбоикосододекаэдрДельтоидальный
гексеконтаэдр
(60 выпуклых дельтоидов)
Слайд 18 (12 квадратов,
8 шестиугольников,
6 восьмиугольников) Ромбоусеченный кубооктаэдрГекзакисоктаэдр
(48 разносторонних треугольников)
Слайд 19 (30 квадратов,
20 шестиугольников,
12 десятиугольников) Ромбоусеченный икосододекаэдрГекзакисикосаэдр
(120 разносторонних треугольников)





























