Презентация на тему Понятие корреляционной зависимости

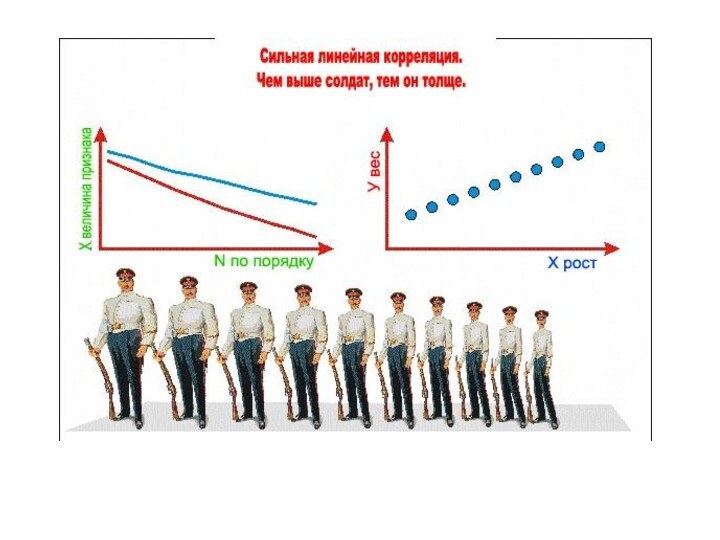
двух признаков. Однако, корреляционные методы не выявляют этой причинности,

а лишь указывают на наличие некоторого соответствия. Признаки могут находиться не только во взаимной зависимости друг от друга, но и оба зависеть от какого-либо третьего воздействия, не включенного в область рассмотрения. Например, между двумя временными рядами (переменные, состоящие из наблюдений отстоящих на равные промежутки времени друг от друга) может быть сильная корреляционная зависимость, однако эта зависимость будет ложной, так как переменные сами зависят от времени.
Таким образом, более корректно употреблять понятие корреляционная связь.

однозначное соответствие аргумента х и функции y=f(х), вероятностная же

зависимость допускает некий условный диапазон, в который предположительно (с такой-то долей вероятности) попадает значение признака уi при значении хi признака х.

связи между признаками,


де хi — значения, принимаемые в

выборке X,
yi — значения, принимаемые в выборке Y;
— средняя по X, — средняя по Y.
Ведем обозначения: ковариация признаков X иY



Средние квадратичные отклонения и

Тогда:

r>0,70;
средняя при 0,50

r<0,19.
Если коэффициент корреляции положительный, то связь между признаками прямая: увеличение одного признака приводит к увеличению другого
Если коэффициент корреляции отрицательный, то связь между признаками обратная: увеличение одного признака приводит к уменьшению другого
В случае, если r=1, -1, то связь между признаками функциональная!

невозможно измерить точно, но он позволяет сравнить объекты между

собой и расположить их в порядке убывания или возрастания качества.
Под ранжированием будем понимать упорядочивание объектов согласно убыванию качественного признака
Для оценки степени связи качественных признаков используют коэффициенты ранговой корреляции.
Коэффициент корреляции Спирмена — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги.
Коэффициент корреляции Кендалла — мера линейной связи между случайными величинами

или две иерархии признаков будут участвовать в сопоставлении как

переменные X и Y.
Проранжировать значения переменной X, присваивая ранг 1 наименьшему значению, и т.д. Занести ранги в первый столбец таблицы по порядку номеров испытуемых или признаков.
Проранжировать значения переменной У, в соответствии с теми же правилами. Занести ранги во второй столбец таблицы по порядку номеров испытуемых или признаков.
Подсчитать разности d между рангами X и Y по каждой строке таблицы и занести в третий столбец таблицы.
Возвести каждую разность в квадрат: d2. Эти значения занести в четвертый столбец таблицы.
Подсчитать сумму d2.
При наличии одинаковых рангов рассчитать поправки:
где a - объем каждой группы одинаковых рангов в
ранговом ряду X; b - объем каждой группы одинаковых
рангов в ранговом ряду Y.

формуле:
при отсутствии одинаковых рангов

при наличии одинаковых рангов

где sum(d2) - сумма квадратов разностей между рангами; Ta и Tb - поправки на одинаковые ранги; N - количество наблюдений признаков, участвовавших в ранжировании.

Схема нахождения коэффициента Корреляции Спирмена

гипотезы имеют вид:
Н0: коэффициент ранговой корреляции Спирмена rs незначимый;
Н1:

коэффициент ранговой корреляции Спирмена rs значим.
Расчитывается t-статистика по формуле:




Определяется tтабл по таблице Стьюдента со степенями свободы n-2 и уровнем значимости α
Если , то Н0 отклоняют на заданном уровне значимости, и считаем, что коэффициент ранговой корреляции Спирмена значимый.