Слайд 2
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
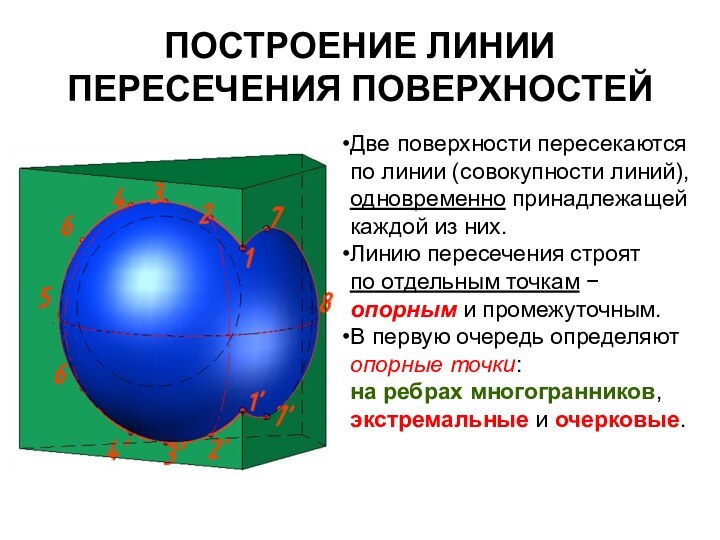
Две поверхности пересекаются по
линии (совокупности линий),
одновременно принадлежащей каждой из них.
Линию
пересечения строят
по отдельным точкам опорным и промежуточным.
В первую очередь определяют опорные точки:
на ребрах многогранников, экстремальные и очерковые.
Слайд 3
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
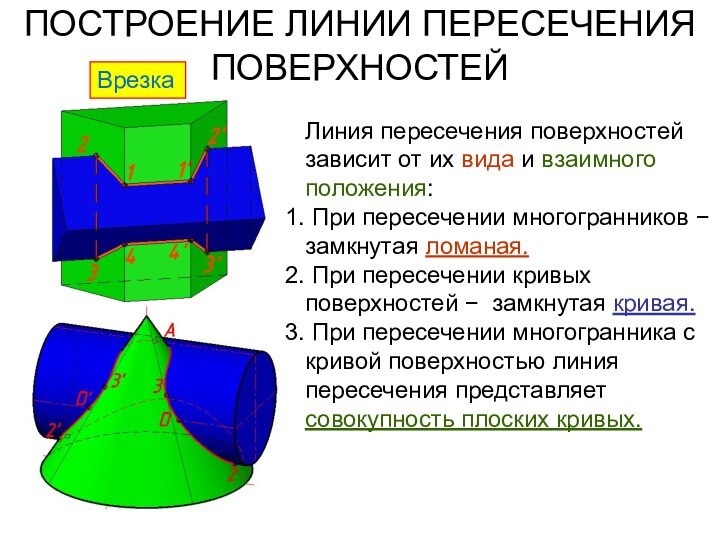
Линия пересечения поверхностей зависит
от их вида и взаимного положения:
При пересечении многогранников
замкнутая ломаная.
При пересечении кривых поверхностей замкнутая кривая.
При пересечении многогранника с кривой поверхностью линия пересечения представляет совокупность плоских кривых.
Врезка
Слайд 4
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
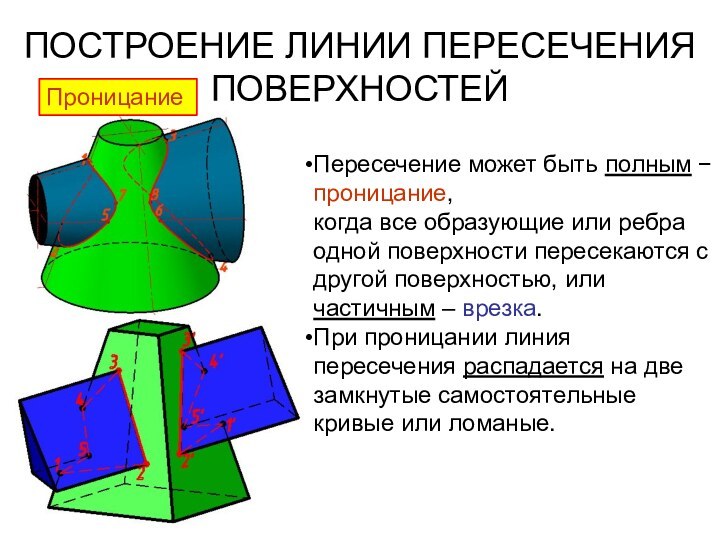
Пересечение может быть полным
проницание,
когда все образующие или ребра одной поверхности
пересекаются с другой поверхностью, или частичным – врезка.
При проницании линия пересечения распадается на две замкнутые самостоятельные кривые или ломаные.
Проницание
Слайд 5
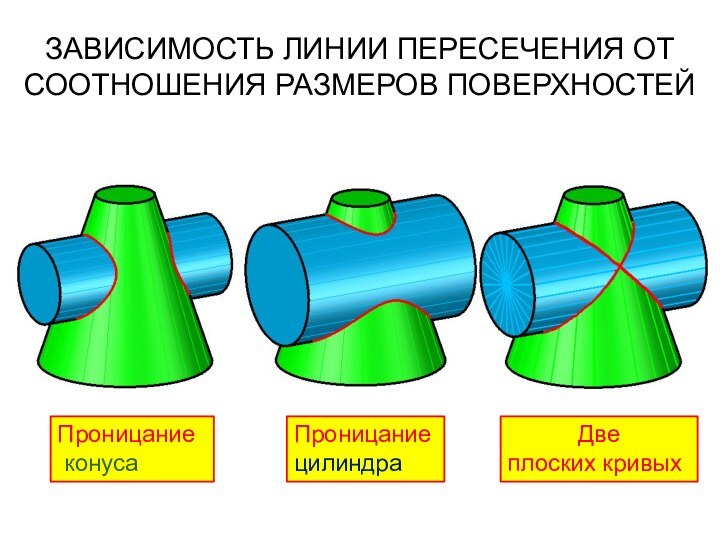
ЗАВИСИМОСТЬ ЛИНИИ ПЕРЕСЕЧЕНИЯ ОТ СООТНОШЕНИЯ РАЗМЕРОВ ПОВЕРХНОСТЕЙ
Проницание
конуса
Проницание цилиндра
Две
плоских кривых
Слайд 6
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
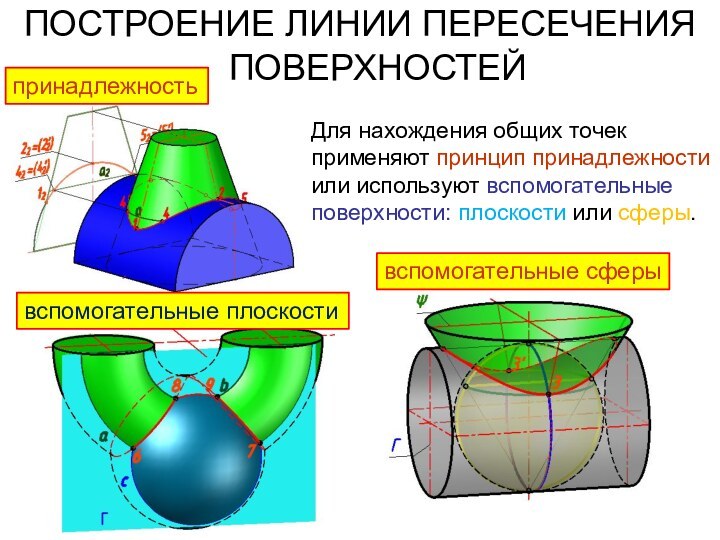
Для нахождения общих точек
применяют принцип принадлежности
или используют вспомогательные поверхности: плоскости или сферы.
принадлежность
вспомогательные
сферы
вспомогательные плоскости
Слайд 7
Последовательность решения задач
на построение линии пересечения поверхностей:
выясняем
вид и расположение заданных поверхностей относительно друг друга (врезка
или проницание)
и плоскостей проекций (задана ли проецирующая поверхность);
определяем характер линии пересечения: замкнутая ломаная, совокупность плоских кривых, замкнутая кривая;
определяем опорные точки (на ребрах многогранников, экстремальные и очерковые);
определяем промежуточные точки (если строим кривую линию);
соединяем найденные точки (ломаной, или кривой),
обводим чертеж с учетом видимости проекций линии пересечения и очерков поверхностей.
Слайд 8
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ
Слайд 9
Построение линии пересечения многогранников
Линия пересечения многогранников
замкнутая пространственная ломаная линия (случай врезки),
или две замкнутые
ломаные (случай проницания).
Вершины ломаной точки пересечения ребер первого многогранника с гранями второго и ребер второго многогранника с гранями первого, а звенья ломаной линии пересечения граней многогранников.
Решение задачи заключается в нахождении вершин или сторон ломаной. В первом случае задача сводится к многократному построению точки пересечения прямой (ребра) с плоскостью,
во втором к многократному построению линии пересечения двух плоскостей.
После определения вершин ломаной (опорных точек) соединяем отрезками прямых те пары вершин, которые принадлежат одной и той же грани первого многогранника и одновременно одной и той же грани второго с учетом видимости.
Слайд 10
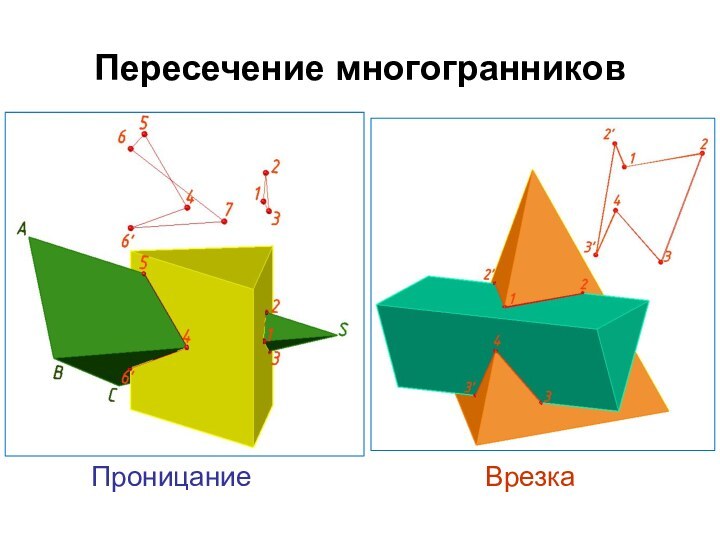
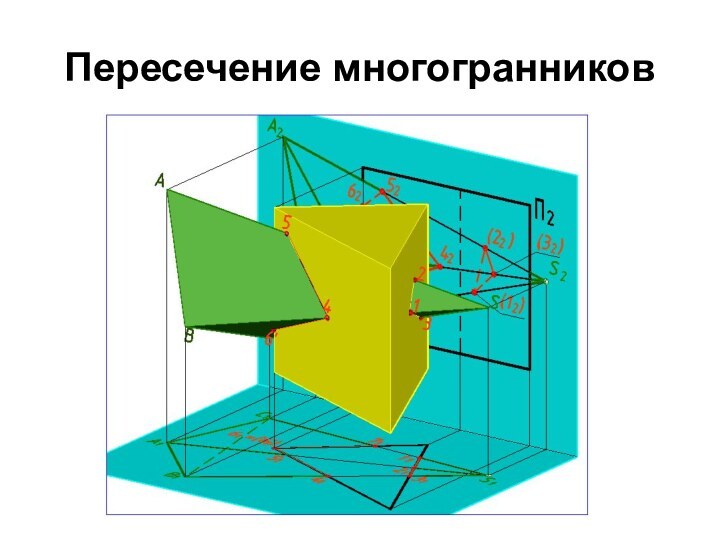
Пересечение многогранников
Проницание
Врезка
Слайд 11
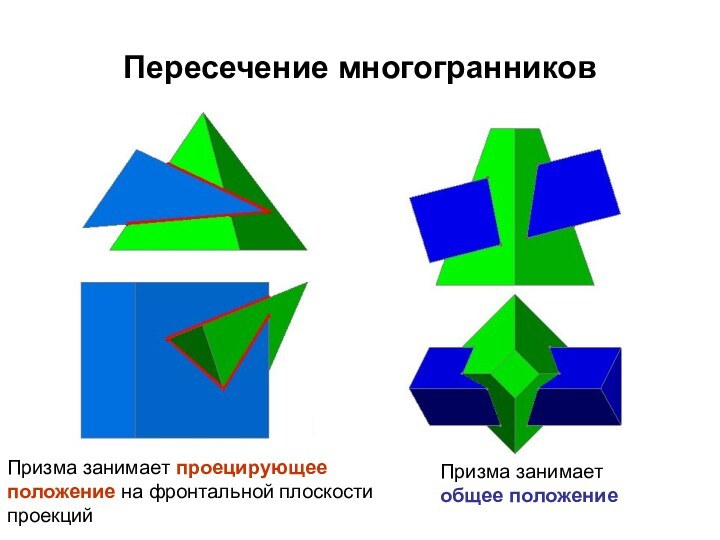
Пересечение многогранников
Призма занимает проецирующее положение на фронтальной плоскости
проекций
Призма занимает
общее положение
Слайд 12
Пересечение многогранников
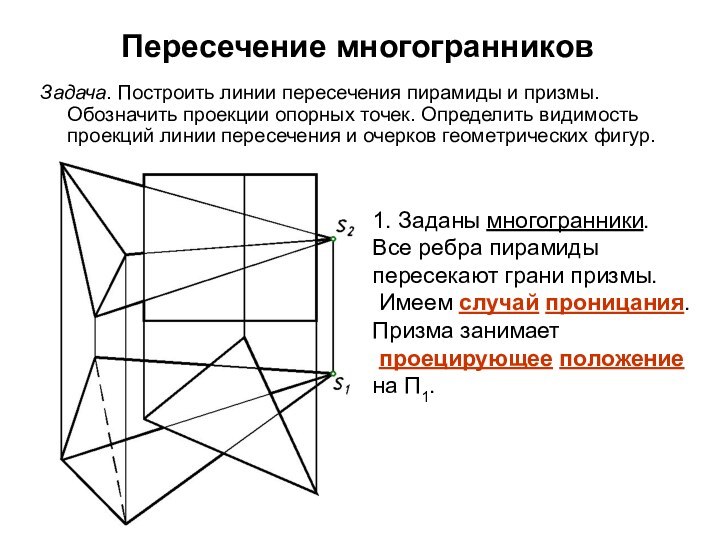
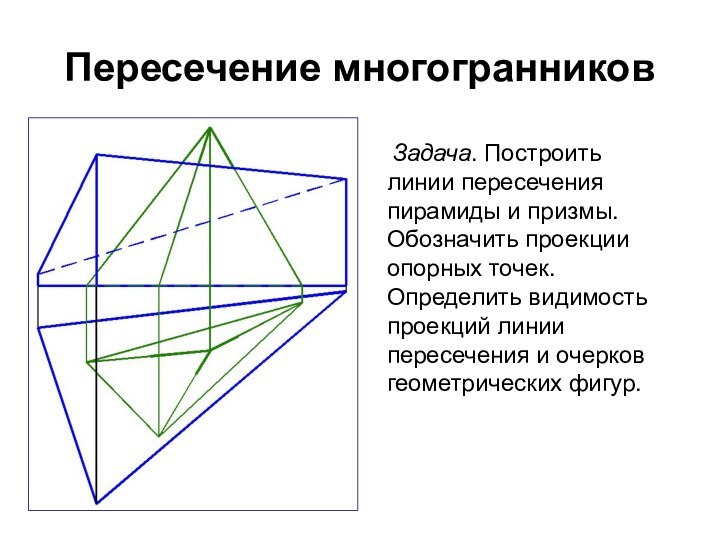
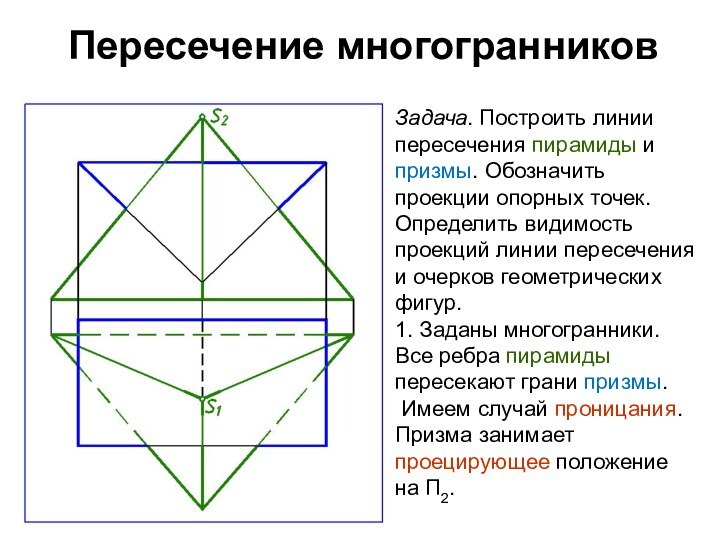
Задача. Построить линии пересечения пирамиды и призмы.
Обозначить проекции опорных точек. Определить видимость проекций линии пересечения
и очерков геометрических фигур.
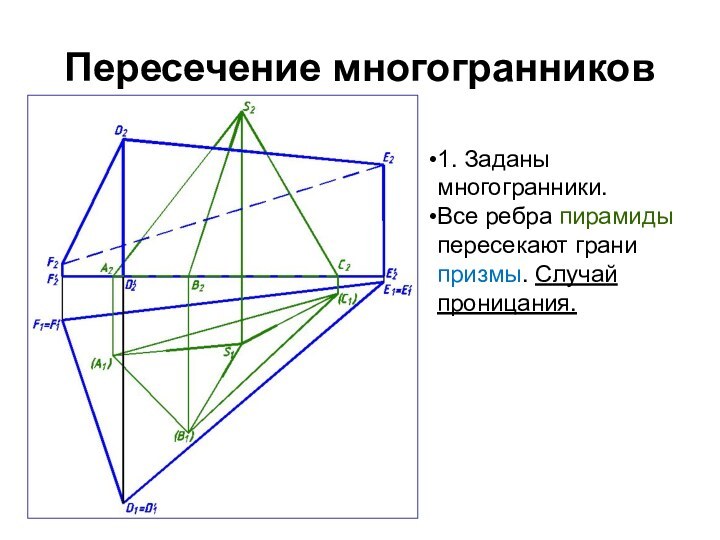
1. Заданы многогранники.
Все ребра пирамиды пересекают грани призмы.
Имеем случай проницания.
Призма занимает
проецирующее положение на П1.
Слайд 13
Пересечение многогранников
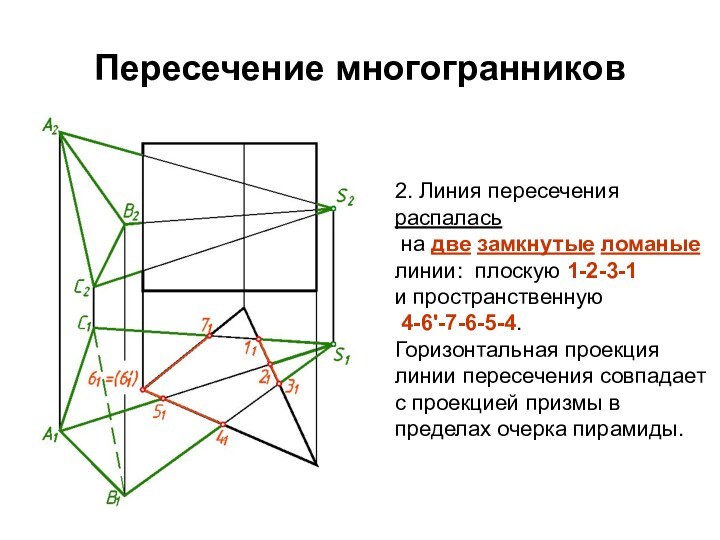
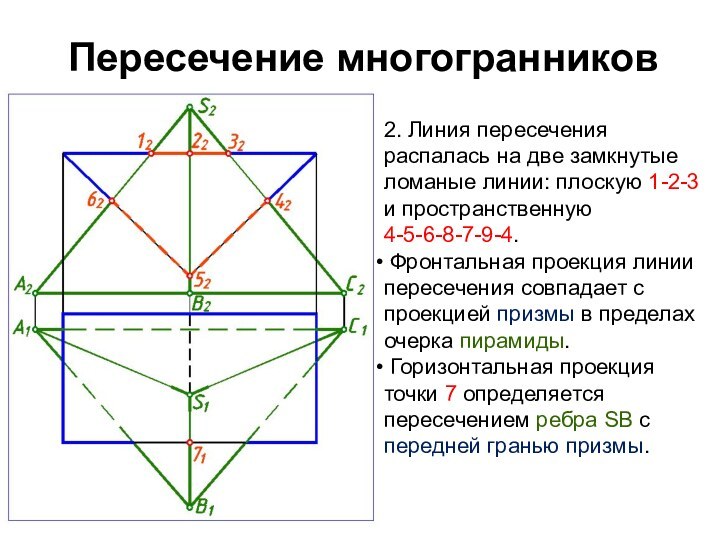
2. Линия пересечения распалась
на две замкнутые
ломаные линии: плоскую 1-2-3-1
и пространственную
4-6'-7-6-5-4.
Горизонтальная проекция
линии пересечения совпадает с проекцией призмы в пределах очерка пирамиды.
Слайд 14
Пересечение многогранников
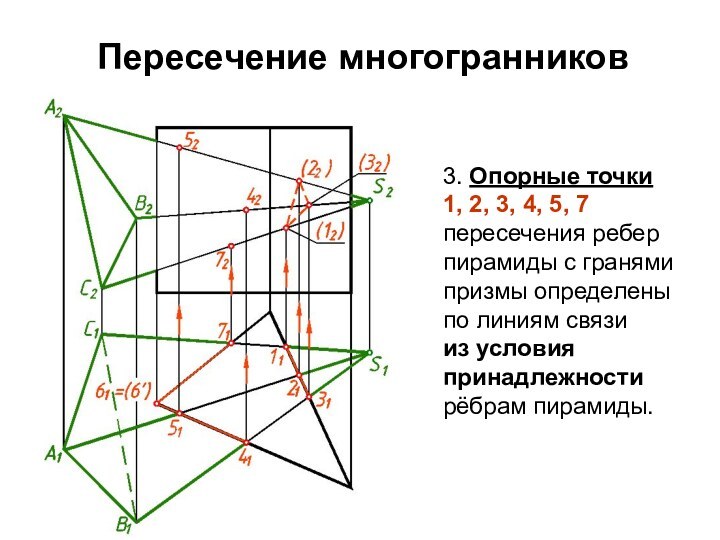
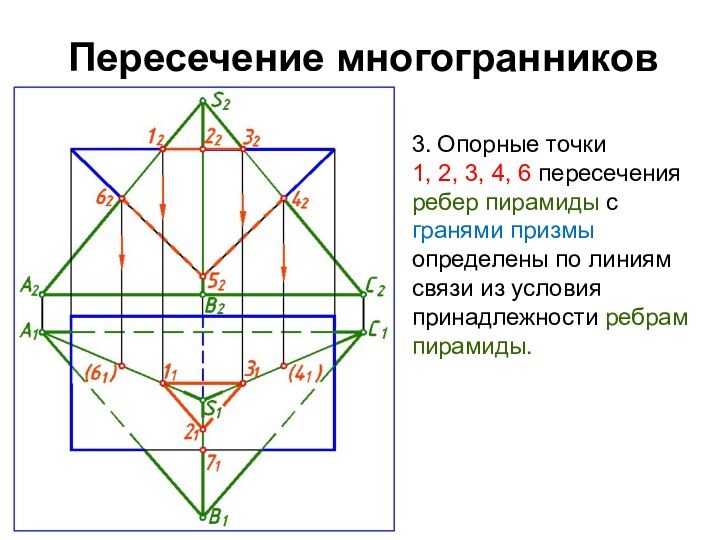
3. Опорные точки
1, 2, 3, 4,
5, 7 пересечения ребер пирамиды с гранями призмы определены
по линиям связи
из условия принадлежности рёбрам пирамиды.
Слайд 15
Пересечение многогранников
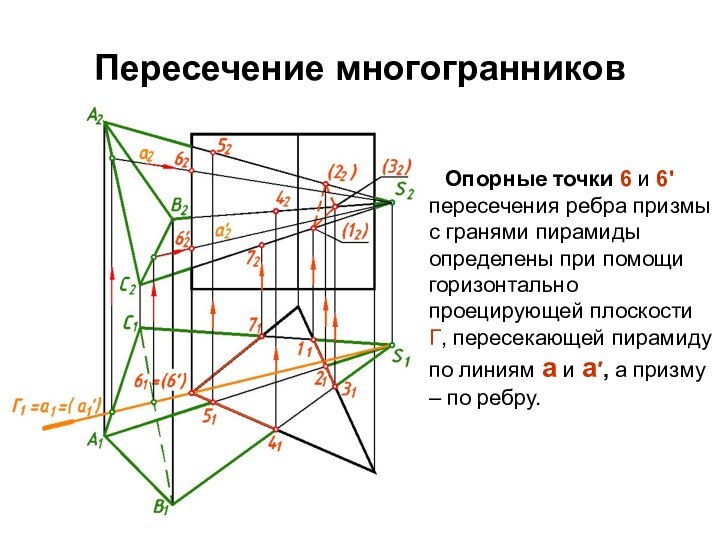
Опорные точки 6 и 6'
пересечения ребра призмы с гранями пирамиды определены при помощи
горизонтально проецирующей плоскости Г, пересекающей пирамиду по линиям а и а′, а призму – по ребру.
Слайд 16
Пересечение многогранников
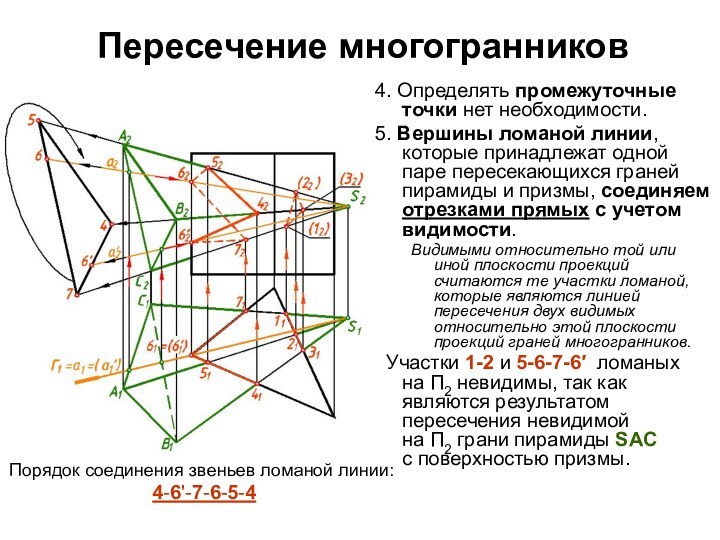
4. Определять промежуточные точки нет необходимости.
5. Вершины
ломаной линии, которые принадлежат одной паре пересекающихся граней пирамиды
и призмы, соединяем отрезками прямых с учетом видимости.
Видимыми относительно той или иной плоскости проекций считаются те участки ломаной, которые являются линией пересечения двух видимых относительно этой плоскости проекций граней многогранников.
Участки 1-2 и 5-6-7-6′ ломаных
на П2 невидимы, так как являются результатом пересечения невидимой
на П2 грани пирамиды SАC
с поверхностью призмы.
Порядок соединения звеньев ломаной линии:
4-6'-7-6-5-4
Слайд 18
Пересечение многогранников
Задача. Построить линии пересечения пирамиды и
призмы. Обозначить проекции опорных точек. Определить видимость проекций линии
пересечения и очерков геометрических фигур.
Слайд 19
Пересечение многогранников
1. Заданы многогранники.
Все ребра пирамиды пересекают
грани призмы. Случай проницания.
Слайд 20
Пересечение многогранников
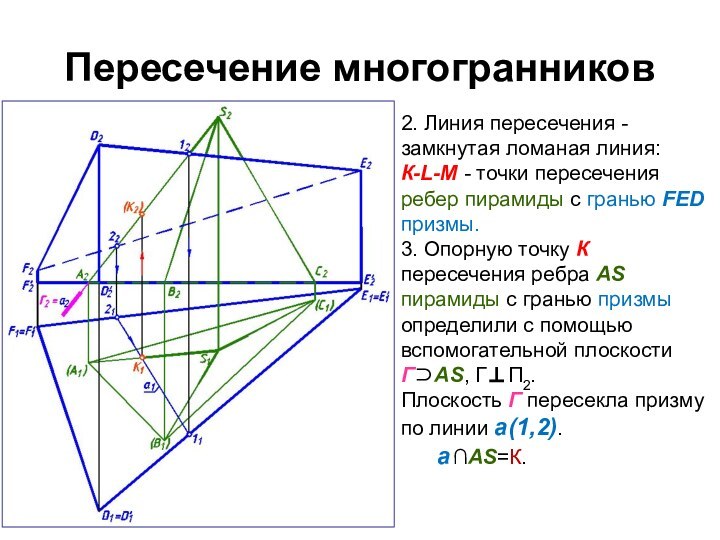
2. Линия пересечения - замкнутая ломаная линия:
К-L-M - точки пересечения ребер пирамиды с гранью FED
призмы.
3. Опорную точку К пересечения ребра АS пирамиды с гранью призмы определили с помощью вспомогательной плоскости ГАS, ГП2.
Плоскость Г пересекла призму по линии а(1,2).
а ∩АS=К.
Слайд 21
Пересечение многогранников
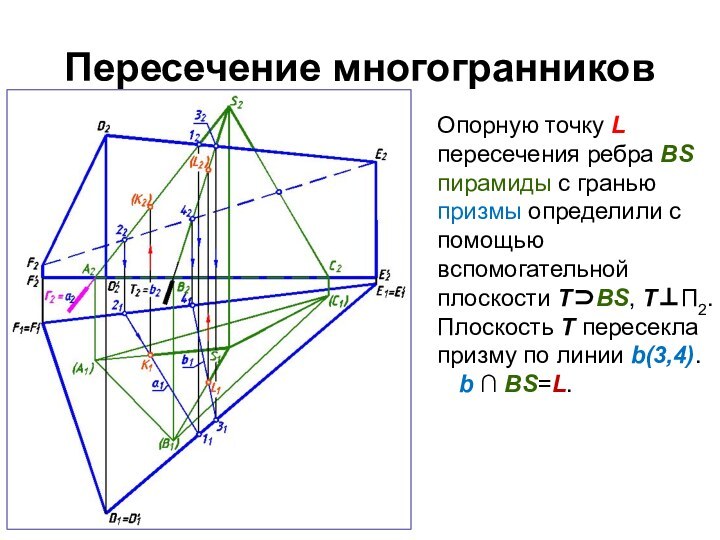
Опорную точку L пересечения ребра ВS пирамиды
с гранью призмы определили с помощью вспомогательной плоскости ТВS,
ТП2.
Плоскость Т пересекла призму по линии b(3,4).
b ∩ ВS=L.
Слайд 22
Пересечение многогранников
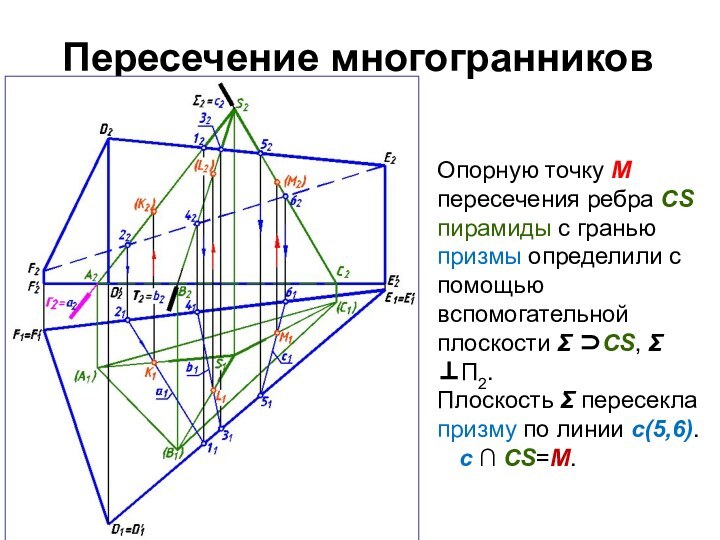
Опорную точку М пересечения ребра СS пирамиды
с гранью призмы определили с помощью вспомогательной плоскости Σ
СS, Σ П2.
Плоскость Σ пересекла призму по линии с(5,6).
с ∩ СS=М.
Слайд 23
Пересечение многогранников
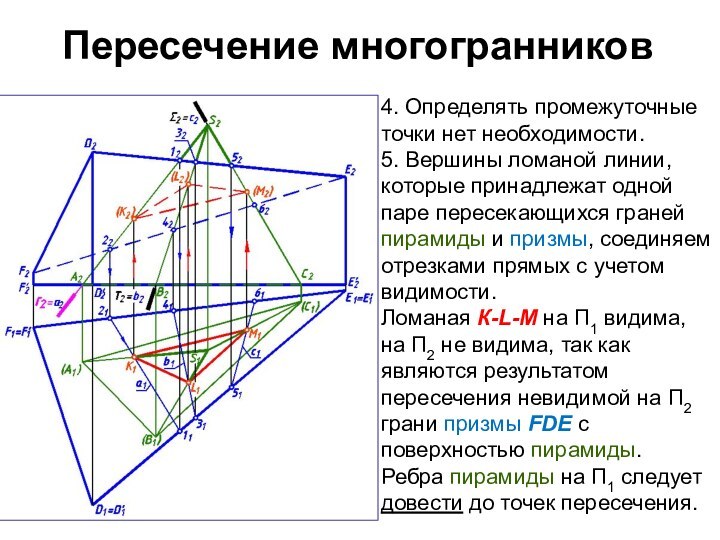
4. Определять промежуточные точки нет необходимости.
5. Вершины
ломаной линии, которые принадлежат одной паре пересекающихся граней пирамиды
и призмы, соединяем отрезками прямых с учетом видимости.
Ломаная К-L-M на П1 видима, на П2 не видима, так как являются результатом пересечения невидимой на П2 грани призмы FDE с поверхностью пирамиды.
Ребра пирамиды на П1 следует довести до точек пересечения.
Слайд 25
Пересечение многогранников
Задача. Построить линии пересечения пирамиды и призмы.
Обозначить проекции опорных точек. Определить видимость проекций линии пересечения
и очерков геометрических фигур.
1. Заданы многогранники.
Все ребра пирамиды пересекают грани призмы.
Имеем случай проницания. Призма занимает проецирующее положение
на П2.
Слайд 27
Пересечение многогранников
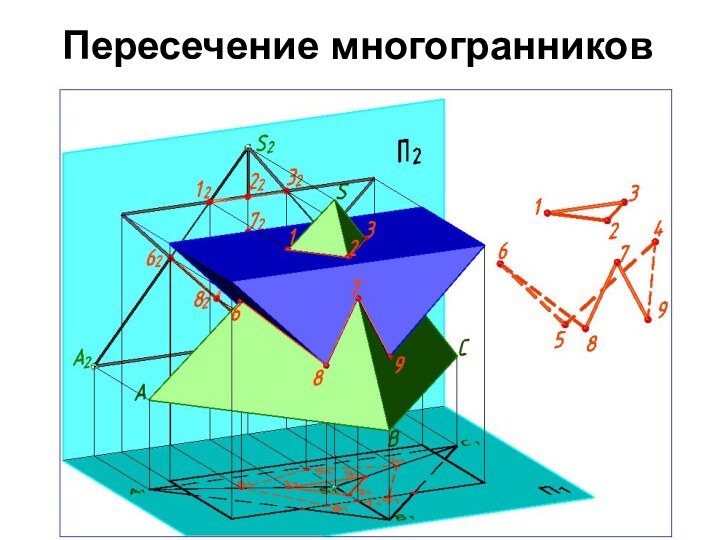
2. Линия пересечения распалась на две замкнутые
ломаные линии: плоскую 1-2-3 и пространственную
4-5-6-8-7-9-4.
Фронтальная проекция
линии пересечения совпадает с проекцией призмы в пределах очерка пирамиды.
Горизонтальная проекция точки 7 определяется пересечением ребра SB с передней гранью призмы.
Слайд 28
Пересечение многогранников
3. Опорные точки
1, 2, 3, 4,
6 пересечения ребер пирамиды с гранями призмы определены по
линиям связи из условия принадлежности ребрам пирамиды.
Слайд 29
Пересечение многогранников
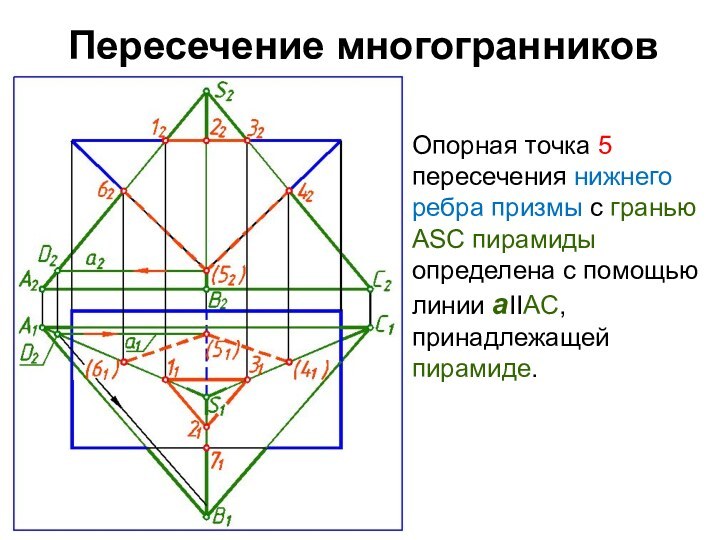
Опорная точка 5 пересечения нижнего ребра призмы
с гранью ASC пирамиды определена с помощью линии аIIAС,
принадлежащей пирамиде.
Слайд 30
Пересечение многогранников
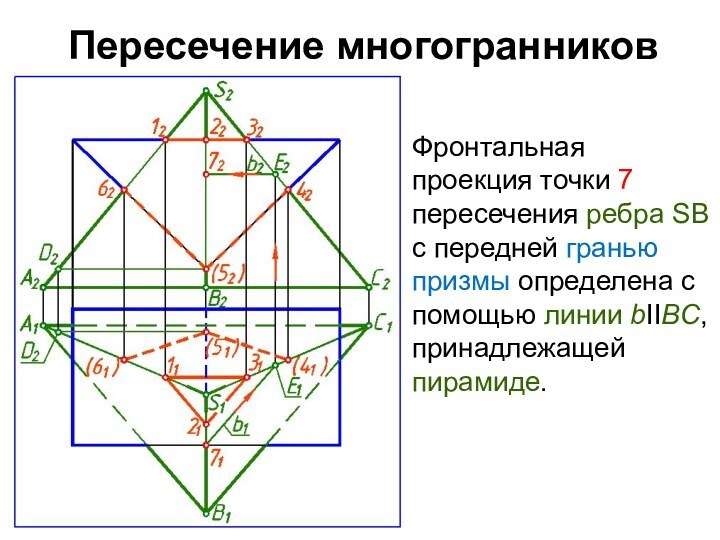
Фронтальная проекция точки 7 пересечения ребра SB
с передней гранью призмы определена с помощью линии bIIBС,
принадлежащей пирамиде.
Слайд 31
Пересечение многогранников
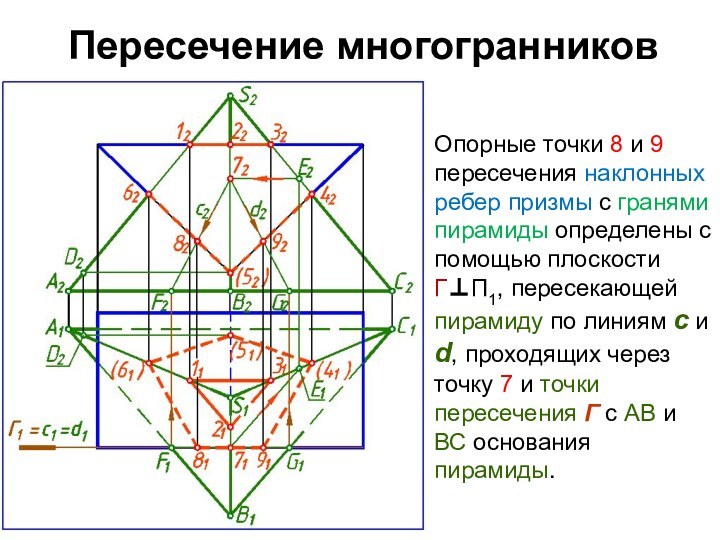
Опорные точки 8 и 9 пересечения наклонных
ребер призмы с гранями пирамиды определены с помощью плоскости
ГП1, пересекающей пирамиду по линиям с и d, проходящих через точку 7 и точки пересечения Г с АВ и ВС основания пирамиды.
Слайд 32
Пересечение многогранников
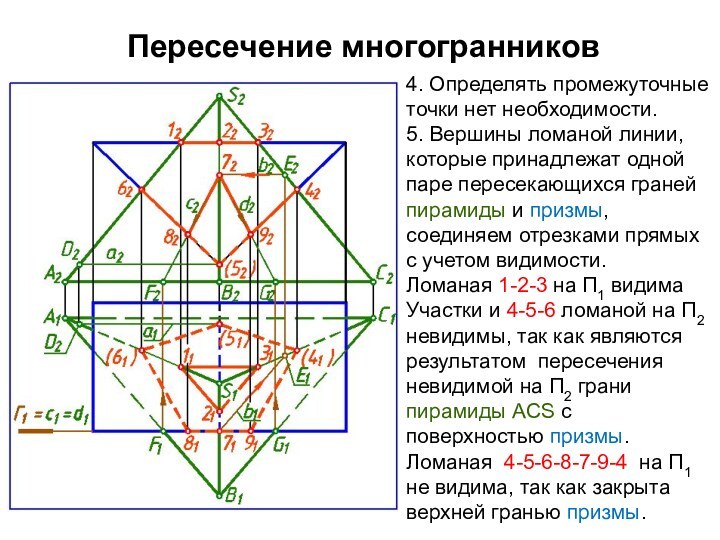
4. Определять промежуточные точки нет необходимости.
5. Вершины
ломаной линии, которые принадлежат одной паре пересекающихся граней пирамиды
и призмы, соединяем отрезками прямых с учетом видимости.
Ломаная 1-2-3 на П1 видима Участки и 4-5-6 ломаной на П2 невидимы, так как являются результатом пересечения невидимой на П2 грани пирамиды АCS с поверхностью призмы. Ломаная 4-5-6-8-7-9-4 на П1 не видима, так как закрыта верхней гранью призмы.
Слайд 33
Пересечение многогранников
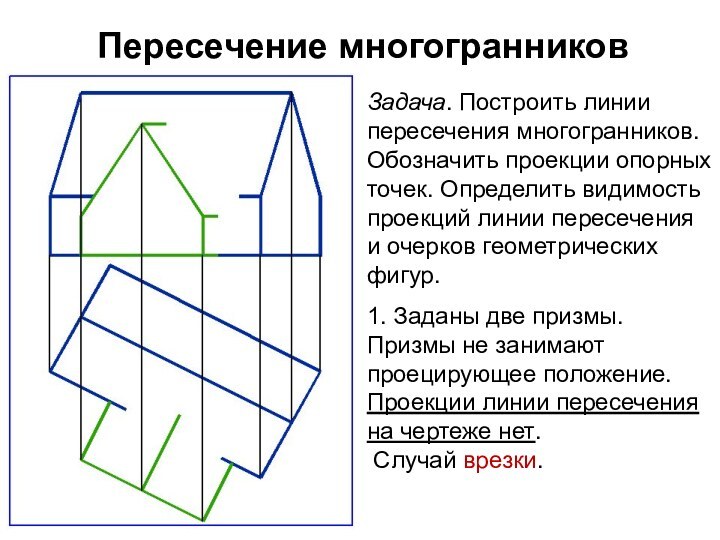
Задача. Построить линии пересечения многогранников. Обозначить проекции
опорных точек. Определить видимость проекций линии пересечения и очерков
геометрических фигур.
1. Заданы две призмы. Призмы не занимают проецирующее положение. Проекции линии пересечения на чертеже нет.
Случай врезки.
Слайд 34
Пересечение многогранников
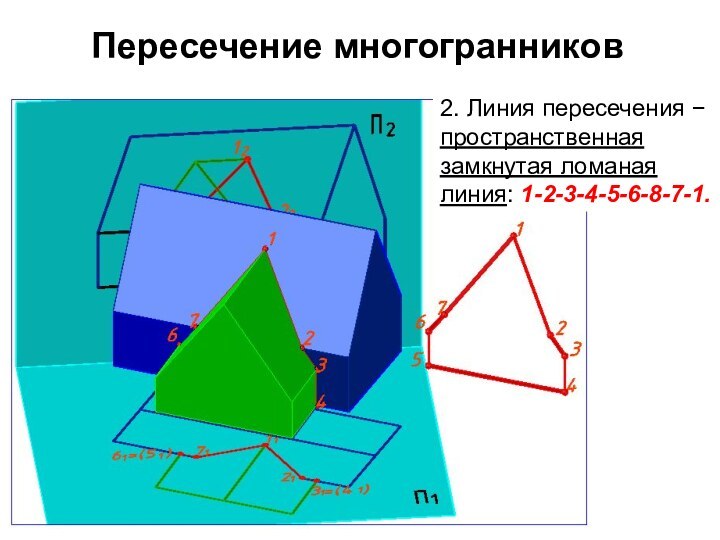
2. Линия пересечения пространственная замкнутая ломаная
линия: 1-2-3-4-5-6-8-7-1.
Слайд 35
Пересечение многогранников
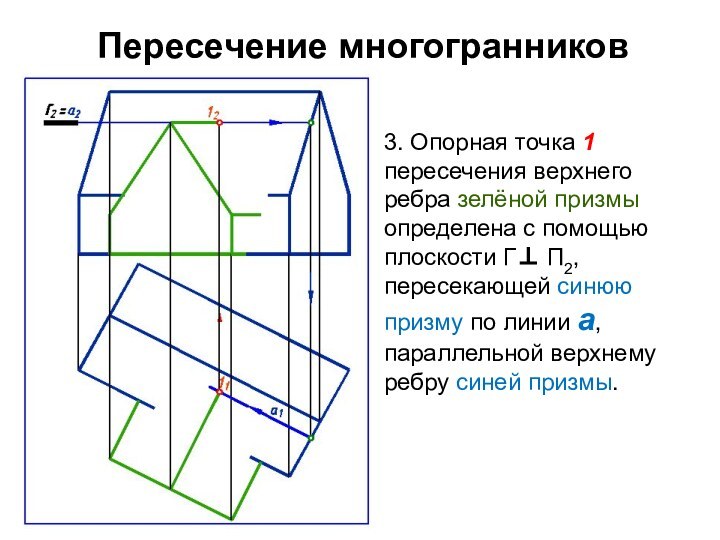
3. Опорная точка 1 пересечения верхнего ребра
зелёной призмы определена с помощью плоскости Г П2, пересекающей
синюю призму по линии а, параллельной верхнему ребру синей призмы.
Слайд 36
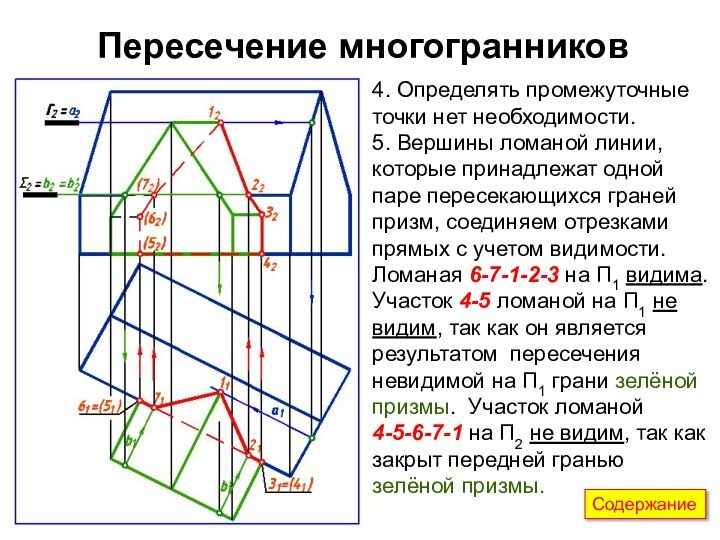
Пересечение многогранников
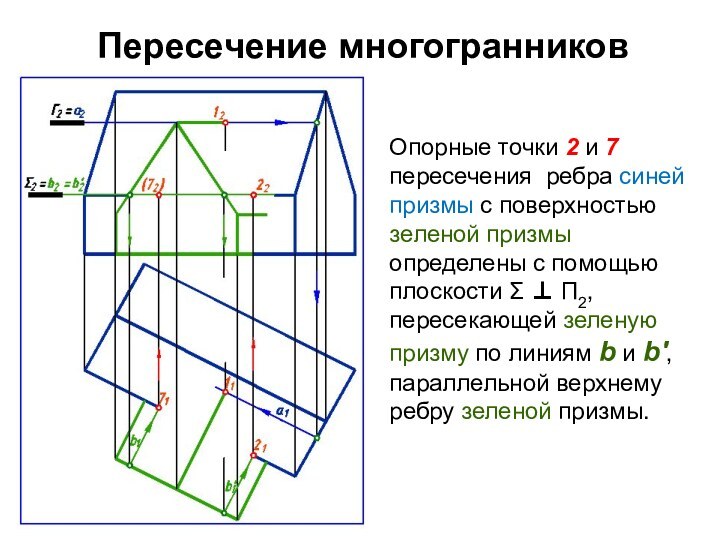
Опорные точки 2 и 7 пересечения ребра
синей призмы с поверхностью зеленой призмы определены с помощью
плоскости Σ П2, пересекающей зеленую призму по линиям b и b', параллельной верхнему ребру зеленой призмы.
Слайд 37
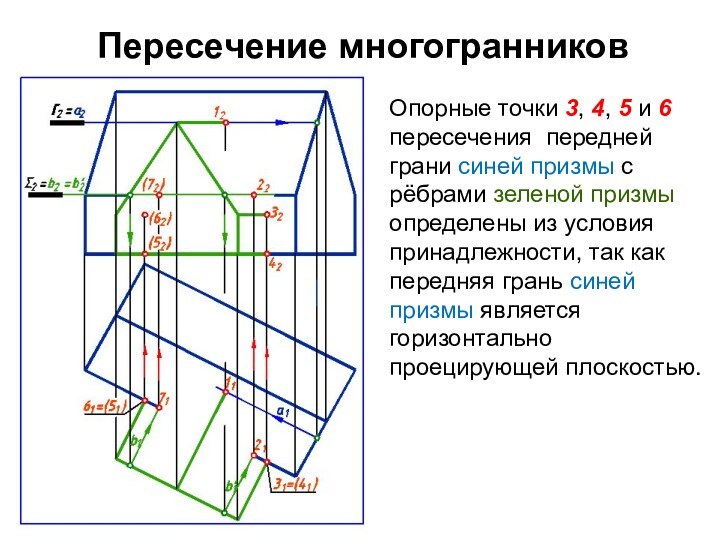
Пересечение многогранников
Опорные точки 3, 4, 5 и 6
пересечения передней грани синей призмы с рёбрами зеленой призмы
определены из условия принадлежности, так как передняя грань синей призмы является горизонтально проецирующей плоскостью.