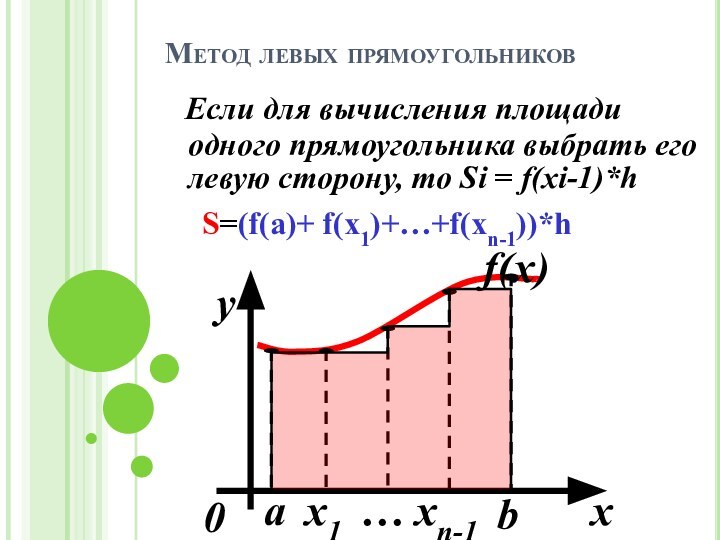
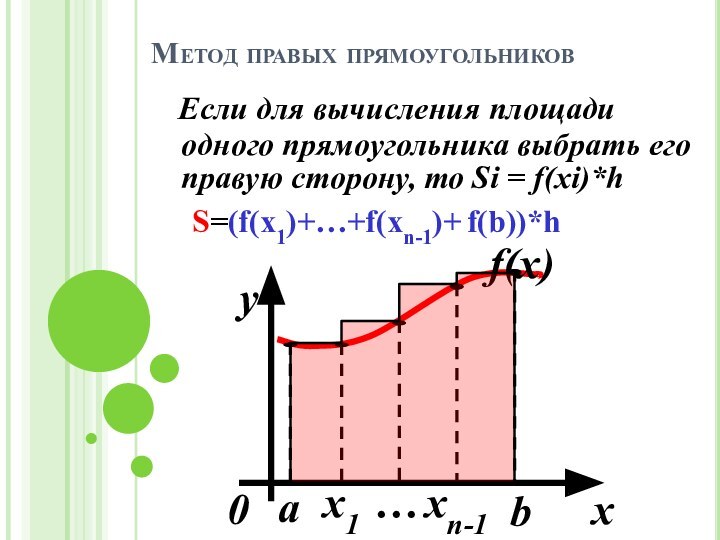
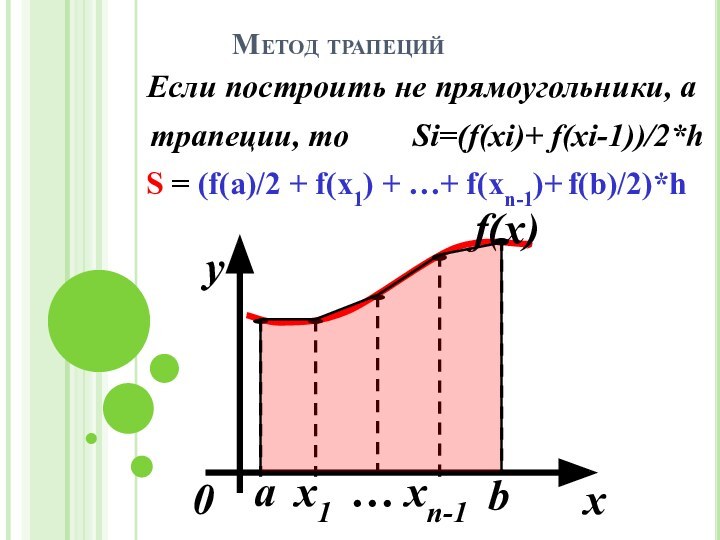
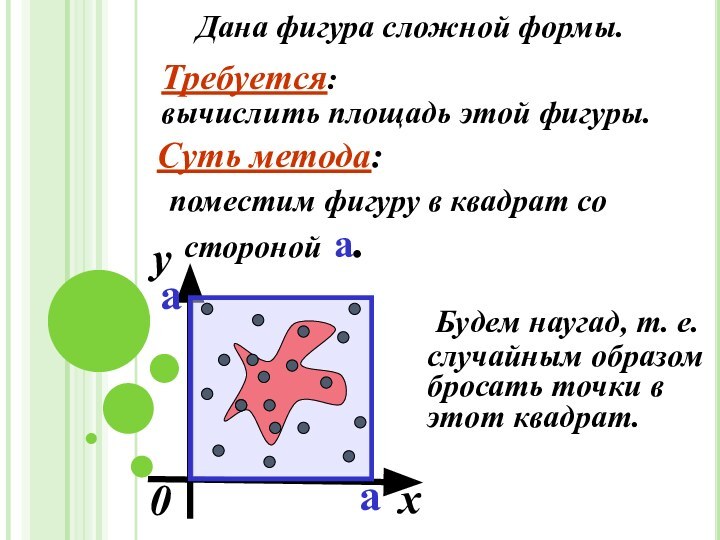
уравнений, представленных в виде f(x)=0.
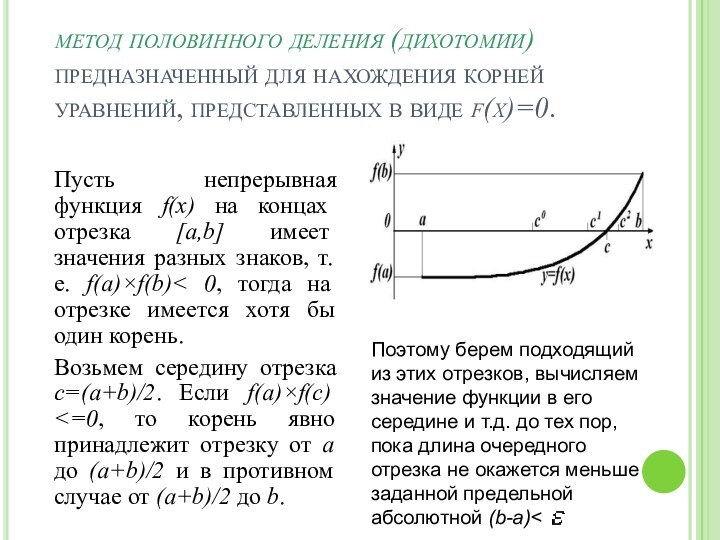
Пусть непрерывная функция f(x)
на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)< 0, тогда на отрезке имеется хотя бы один корень. Возьмем середину отрезка с=(a+b)/2. Если f(a)×f(с) <=0, то корень явно принадлежит отрезку от a до (a+b)/2 и в противном случае от (a+b)/2 до b.
Поэтому берем подходящий из этих отрезков, вычисляем значение функции в его середине и т.д. до тех пор, пока длина очередного отрезка не окажется меньше заданной предельной абсолютной (b-a)<


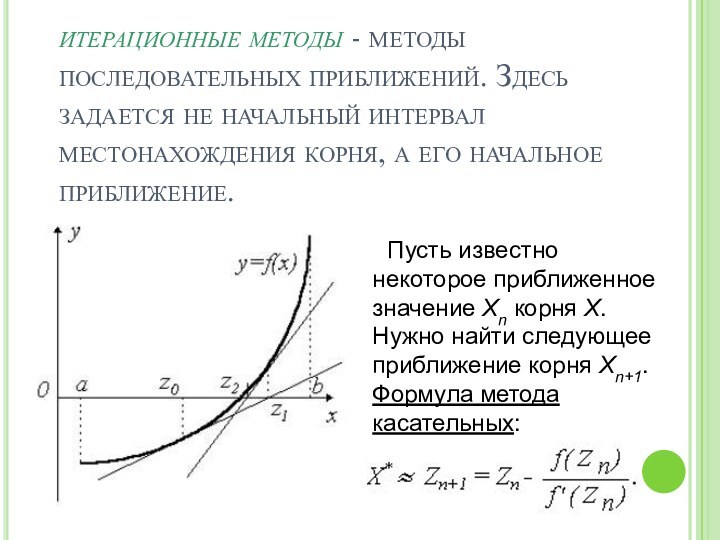
![Решение уравнений с помощью численных методов В качестве исходной точки х выбирается тот конец интервала [a,b], которому ордината](/img/tmb/13/1273699/61cc8dbabcceda567ee5fe5752f8c437-720x.jpg)

![Решение уравнений с помощью численных методов Определённый интеграл Можно трактовать как площадь подынтегральной функции (криволинейной трапеции) на отрезке [a;b]xу0f(x)ab= S](/img/tmb/13/1273699/6e41a86efbb3ee09a1fa9662de1f008a-720x.jpg)

![Решение уравнений с помощью численных методов Пусть функция f(x) определена на отрезке [а;b].Требуется: приближенно вычислить определённый интеграл](/img/tmb/13/1273699/fe96ff5486d25cda09a12a1635a37c67-720x.jpg)