2n) –перебором
решить невозможно.
Примеры NP-трудных задач:
Задача о ранце. –
последовательность из n элементов, каждый из которых может
принимать 2 значения (xi = [0;1])) Число комбинаций 2n
Задача коммивояжера – перестановка из n элементов =(i1, i2, … ,in) (n!).
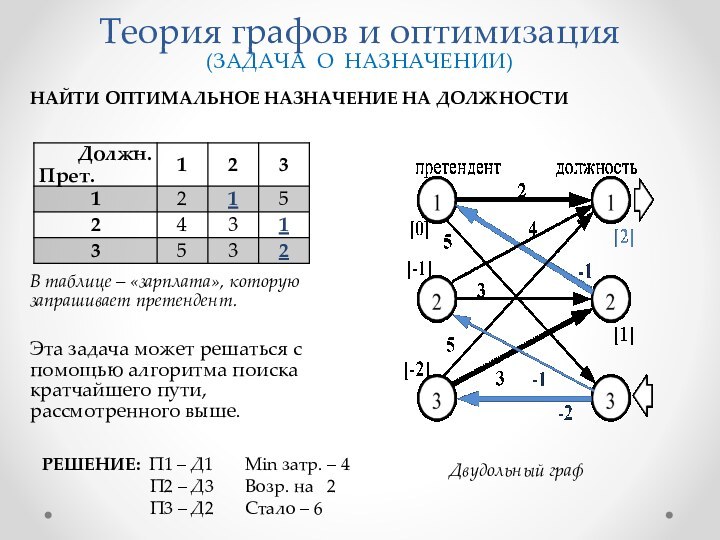
Подбор команды численностью m человек из n претендентов. (Число сочетаний).
Примеры комбинаций
Перестановка (Pn) из n элементов (например чисел 1,2,…,n) – любой упорядоч-
енный набор из элементов. Размещение из n элементов по n – n!.
Размещение (Ank) из n элементов по k – упорядоченный набор из k различных
элементов некоторого n-элементного множества – n!/(n-k)!.
Сочетание из n по k (Cnk) – набор k элементов, выбранных из данных n элементов.
Наборы, отличающиеся только порядком следования элементов (но не
составом), считаются одинаковыми (отличие от размещений) – n!/(n-k)!/k!.
Последовательность – набор из n элементов, каждый из которых может
принимать одно из m значений – mn.
20! = 2,432902 × 1018
(Проверяя по 100 комбинаций в 1 сек. мы потратим около 770 млн. лет)