- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решениеквадратных уравненийразличными способами
Содержание
- 2. Приобретать знания – храбрость,Приумножать их – мудрость,А умело применять – великое искусство.
- 3. Цель работы:Познакомиться с новыми способами решения квадратных уравнений и формировать умение выбора рационального способа решения.
- 4. Задачи:Изучить литературу по проблеме.Расширить и углубить знания
- 5. Гипотеза:Методы исследования:Предполагаю, что освоение новых методов решения
- 6. Проблема: изучение и освоение различных способов решения
- 7. Из истории квадратных уравнений:Необходимость решать такие уравнения
- 8. Впервые квадратное уравнение сумели решить математики Древнего Египта, сводя их решение к геометрическим построениям
- 9. Приемы решения уравнений без обращения к геометрии дает Диофант Александрийский.
- 10. Индийский ученый, Брахмагупта(VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой форме:ах2+вх=с, а0.
- 11. После трудов нидерландского математика А. Жирара
- 12. Что такое квадратное уравнение?Квадратное уравнение – уравнение
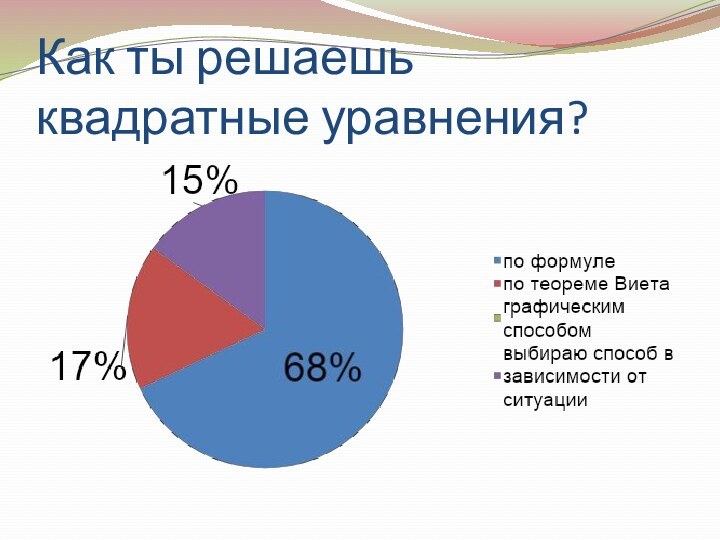
- 13. Как ты решаешь квадратные уравнения?
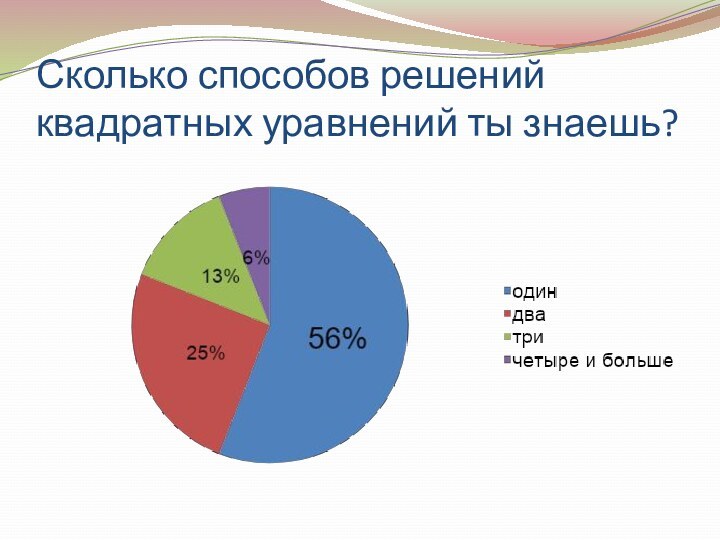
- 14. Сколько способов решений квадратных уравнений ты знаешь?
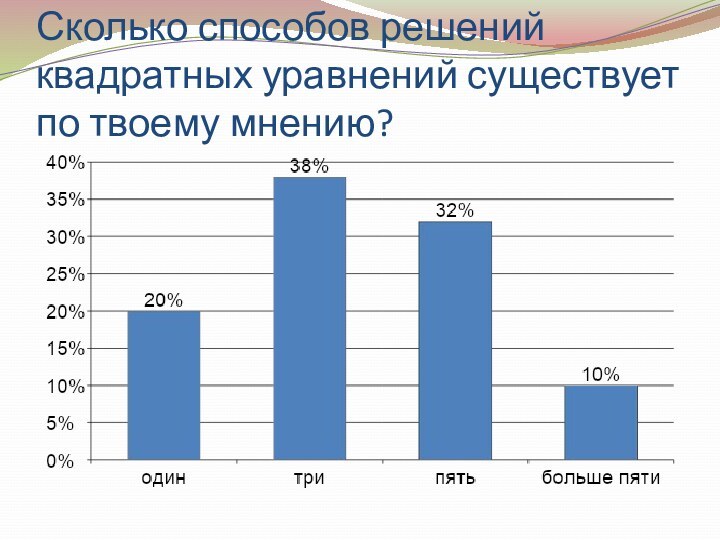
- 15. Сколько способов решений квадратных уравнений существует по твоему мнению?
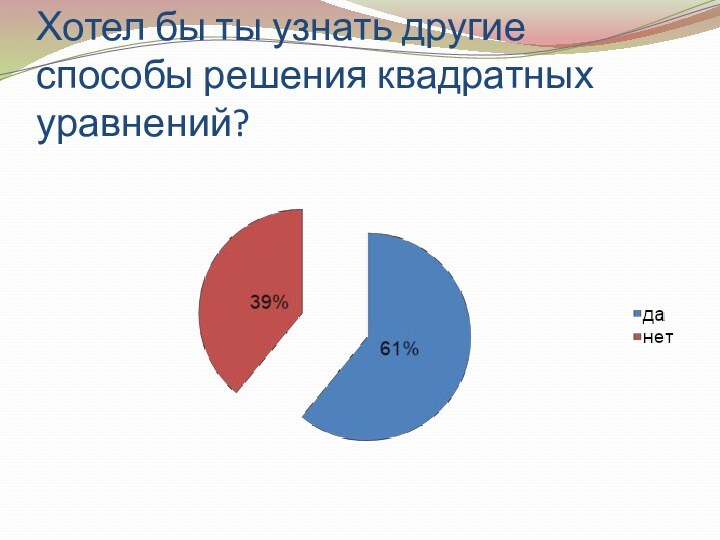
- 16. Хотел бы ты узнать другие способы решения квадратных уравнений?
- 17. Первое свойство коэффициентовВторое свойство коэффициентовТретье свойство коэффициентовС
- 18. Первое свойство коэффициентовЕсли сумма коэффициентов равна нулю,
- 19. Второе свойство коэффициентовЕсли b = а
- 20. Третье свойство коэффициентовЕсли второй коэффициент b четное
- 21. Решение квадратных уравнений с помощью циркуля и
- 22. х2
- 25. Геометрический способ решенияРешим геометрически уравнения у2 –
- 26. Решение уравнений методом «переброски»Рассмотрим квадратное уравнение
- 27. Решение квадратных уравнений с помощью номограммыЭто старый
- 28. х2 –
- 29. Вывод:Во время своих исследований я узнала о
- 31. Скачать презентацию
- 32. Похожие презентации
Приобретать знания – храбрость,Приумножать их – мудрость,А умело применять – великое искусство.























Слайд 2
Приобретать знания – храбрость,
Приумножать их – мудрость,
А умело
применять – великое искусство.
Слайд 3
Цель работы:
Познакомиться с новыми способами решения квадратных уравнений
и формировать умение выбора рационального способа решения.
Слайд 4
Задачи:
Изучить литературу по проблеме.
Расширить и углубить знания по
математике, познакомившись со способами решения квадратных уравнений.
Изучить различные
способы решения.Распространение различных способов.
Слайд 5
Гипотеза:
Методы исследования:
Предполагаю, что освоение новых методов решения квадратных
уравнений позволит выбирать самый рациональный для их решения.
Изучение программного
материала по учебникам А.Г.Мордковича, Н.В.Алимова, Ю.Н.МакарычеваИзучение дополнительного материала по энциклопедиям
Изучение исторического материала по сайтам Интернета
Работа в программах Microsoft Word, Excel, PowerPoint, Publisher
Слайд 6 Проблема: изучение и освоение различных способов решения квадратных
уравнений, способствующих развитию умственных способностей и математического кругозора ученика.
Объект
исследования: раздел математики «Уравнения».Предмет исследования: квадратные уравнения.
Слайд 7
Из истории квадратных уравнений:
Необходимость решать такие уравнения еще
в древности была вызвана потребностью решать задачи, связанные с
нахождением площадей земли, а также с развитием астрономии и математикиСлайд 8 Впервые квадратное уравнение сумели решить математики Древнего Египта,
сводя их решение к геометрическим построениям
Слайд 10 Индийский ученый, Брахмагупта(VII в.), изложил общее правило решения
квадратных уравнений, приведенных к единой форме:
ах2+вх=с, а0.
Слайд 11
После трудов нидерландского математика
А. Жирара
(1595 - 1632), а также Декарта и Ньютона способ
решения квадратных уравнений принял современный вид.
Слайд 12
Что такое квадратное уравнение?
Квадратное уравнение – уравнение вида
ax2 + bx + c = 0,
где х- переменная,
а,b и с-некоторые числа, причем, а ≠ 0.
Если в квадратном уравнении
ах2 + bx + c = 0
хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов:
1) ах2 + с = 0, где b = 0;
2) ах2 + bх = 0, где с = 0;
3) ах2 = 0, где b = 0, c = 0.
Слайд 17
Первое свойство коэффициентов
Второе свойство коэффициентов
Третье свойство коэффициентов
С помощью
циркуля и линейки
Геометрический способ
Методом переброски
С помощью номограммы
Слайд 18
Первое свойство коэффициентов
Если сумма коэффициентов равна нулю, т.е.
а + b + с = 0, то х1
= 1, х2 = .Доказательство: Разделим обе части уравнения на а, получим приведенное квадратное уравнение
Согласно теореме Виета: х1 · х2 = , х1 + х2 = - .
По условию, а + в + с = 0, тогда в = - а - с. Значит,
х1 · х2 = = 1 · , х1 + х2 = - = - = 1 + .
Получаем х1 = 1, х2 = , что и требовалось доказать.
Пример
3х2 + 5х – 8 = 0,
т.к. а + b + с = 0
( 3 + 5 – 8 = 0 ), то получим
х1 = 1, х2 = = -
Ответ: 1 и -
Слайд 19
Второе свойство коэффициентов
Если b = а +
с, то х1 = -1, х2 = -
.Доказательство аналогично первому.
Пример
11х2 + 27х + 16 = 0,
Т.к. b = a + c (27 = 11 + 16 ), значит
х1 = - 1, х2 = - = - .
Ответ: -1 и -
Слайд 20
Третье свойство коэффициентов
Если второй коэффициент b четное число
( b = 2k ), то формулу корней можно
записать в виде .Пример
4х2 – 36х + 77 = 0,
а = 4, b = - 36, с = 77, k = - 18;
D = k2 – ас = ( - 18 )2 – 4 · 77 = 324 – 308 = 16, D > 0, два различных корня;
х1 = 5, 5 , х2 = 3,5.
Ответ: 5,5 и 3,5.
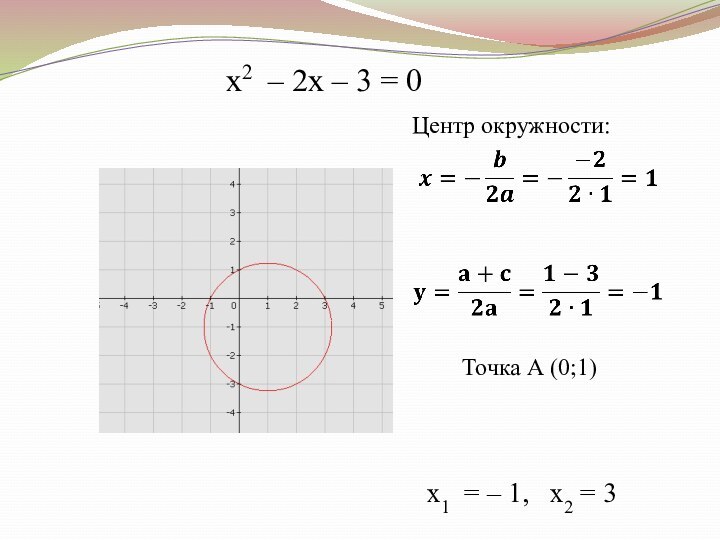
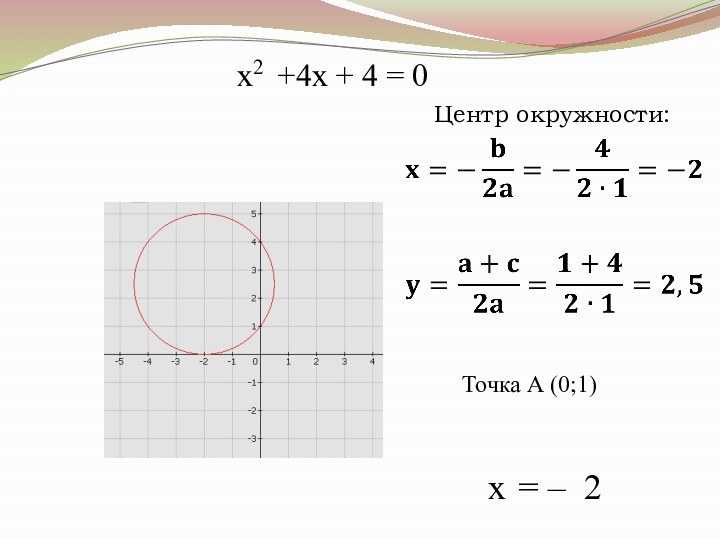
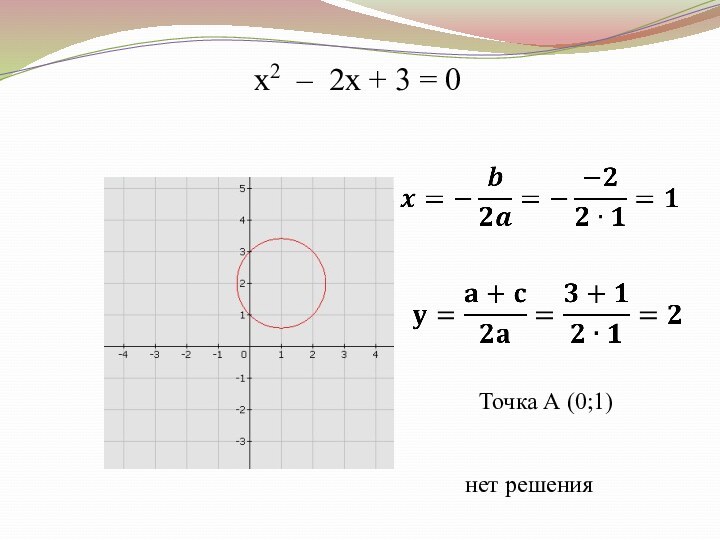
Слайд 21
Решение квадратных уравнений с помощью циркуля и линейки:
Центр
окружности:
Точка А (0;1)
ax2 + bx + c = 0
SA
– радиус окружностит.S (x;y) – центр окружности
-
Слайд 25
Геометрический способ решения
Решим геометрически уравнения у2 – 6у
– 16 = 0.
Преобразуя уравнение, получаем у2 – 6у
= 16.В левой части уравнения выделяем полный квадрат и получаем
y2 + 6y + 9 = 16 + 9, отсюда получаем (y + 3)2 =25.
Следовательно, y + 3 = ±5, откуда y1 = 2, y2 = -8.
Слайд 26
Решение уравнений методом «переброски»
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х = ; тогда приходим к уравнению
у2 + by + ас = 0,
равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = и х2 = . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
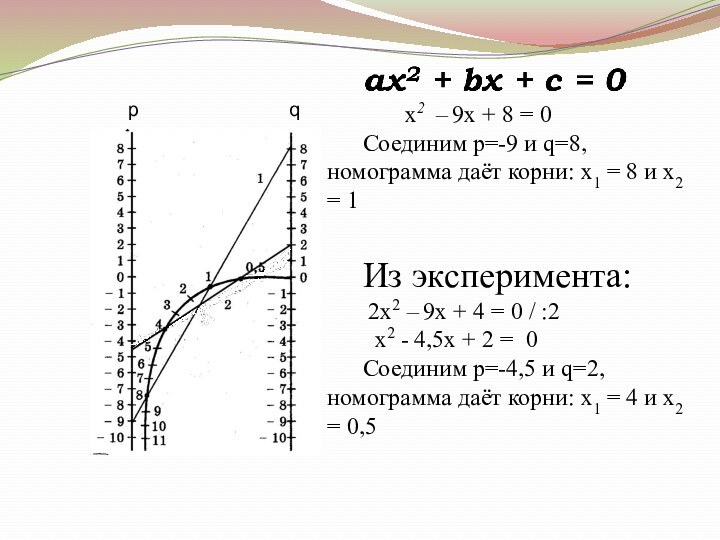
Слайд 27
Решение квадратных уравнений с помощью номограммы
Это старый и
незаслуженно забытый способ решения квадратных уравнений, помещенный на с.83
таблиц Брадиса.
Слайд 28
х2 – 9х
+ 8 = 0
Соединим p=-9 и q=8, номограмма даёт
корни: х1 = 8 и х2 = 1Из эксперимента:
2х2 – 9х + 4 = 0 / :2
х2 - 4,5х + 2 = 0
Соединим p=-4,5 и q=2, номограмма даёт корни: х1 = 4 и х2 = 0,5
p q
Слайд 29
Вывод:
Во время своих исследований я узнала о 7
новых способах решения
квадратных уравнений. Я надеюсь, что они помогут
и мне, и моимодноклассникам в будущем.Я считаю, что своей цели я достигла. Но
также я узнала, что существует около 100 способов решения
квадратных уравнений. Поэтому, я думаю, что буду продолжать свои
исследования в более старших классах.





























