Презентация на тему Сборник задач по планиметрии.

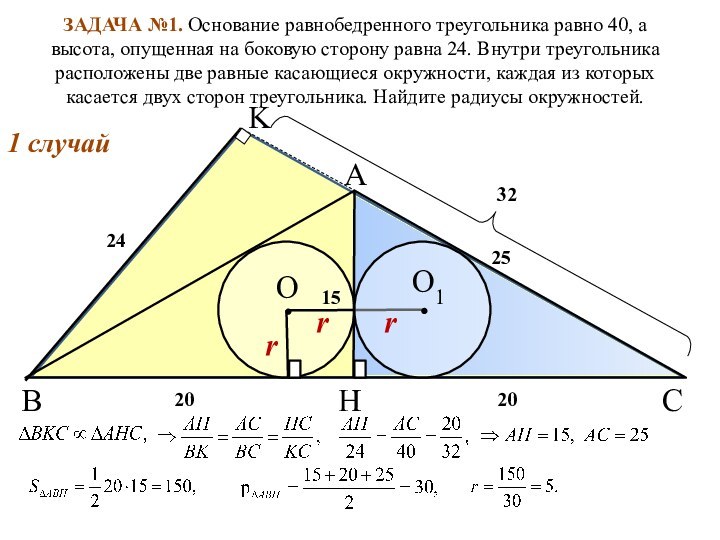
высота, опущенная на боковую сторону равна 24. Внутри треугольника

расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

В

С

Н

А

О

r

r

1 случай

20

24

K

32

О1

r

20

25

15

на боковую сторону равна 3. Внутри треугольника расположены две

равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.


Основание равнобедренного треугольника равно 5, а высота, опущенная на боковую сторону равна 4. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.


Основание равнобедренного треугольника равно 80, а высота, опущенная на боковую сторону равна 64. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

Задачи для самостоятельного решения

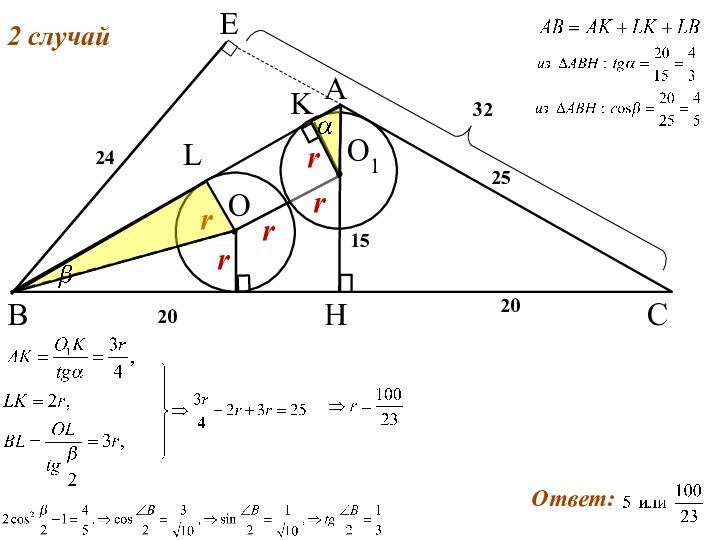
Ответ:

Ответ:

Ответ:

и 20. Внутри него расположены две равные касающиеся окружности,

каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

В

С

Н

О1

r

А

О

r

r

1 случай

26

10

115 и 184. Внутри него расположены две равные касающиеся

окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.


Дан треугольник со сторонами 30, 30 и 36. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.


Дан треугольник со сторонами 13, 13 и 10. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

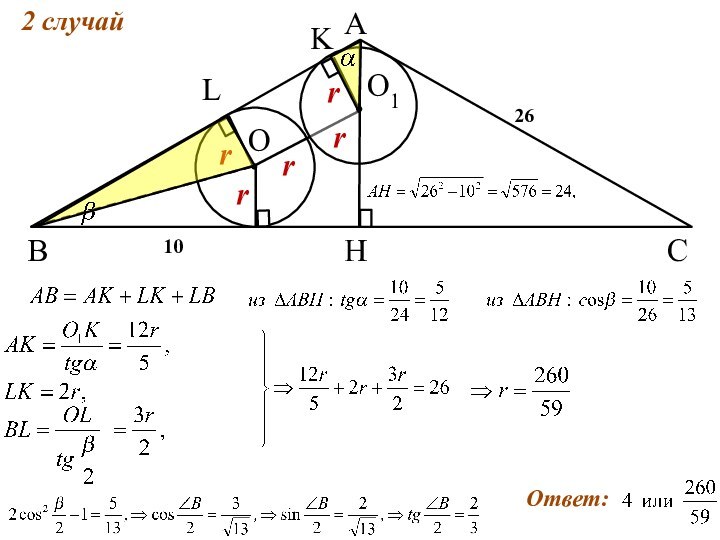
Ответ:

Ответ:

Ответ:

ВС=6, АC=7. Окружность, проходящая через точки А и С,

пересекает прямые ВА и ВС соответственно в точках К и L , отличных от вершин треугольника. Отрезок КL касается окружности, вписанной в треугольник АBC. Найдите длину отрезка KL.

A

B

C

K

L

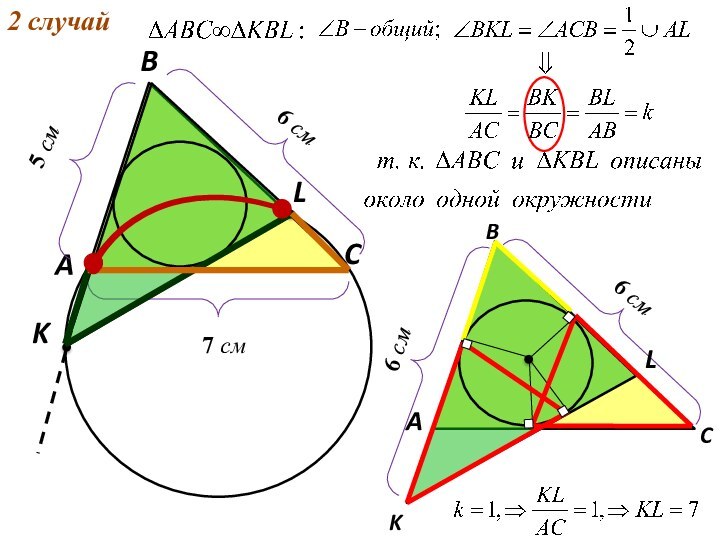
5 см

6 см

7 см

A

B

C

K

L

5 см

6 см

7 см

1 Случай

2 Случай

АВ = 4, ВС = 6, АС = 5.

Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.


В треугольнике ABC известны стороны: АВ = 7, ВС = 10, АС = 8. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.


В треугольнике ABC известны стороны: АВ = 5, ВС = 7, АС = 8. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.

Ответ:

Ответ:

Ответ:

ВС = 10, АС =11. Окружность, проходящая через точки

A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.


В треугольнике ABC известны стороны: АВ = 8, ВС = 10, АС = 11. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.


В треугольнике ABC известны стороны: АВ = 7, ВС = 9, АС = 10. Окружность, проходящая через точки A и С, пересекает прямые ВА и BС соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в треугольник ABC. Найдите длину отрезка KL.

Задачи для самостоятельного решения

Ответ:

Ответ:

Ответ:

равен 5/13, а боковая сторона равна 39. Внутри треугольника

расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

В

С

Н

О1

r

А

О

r

r

1 случай

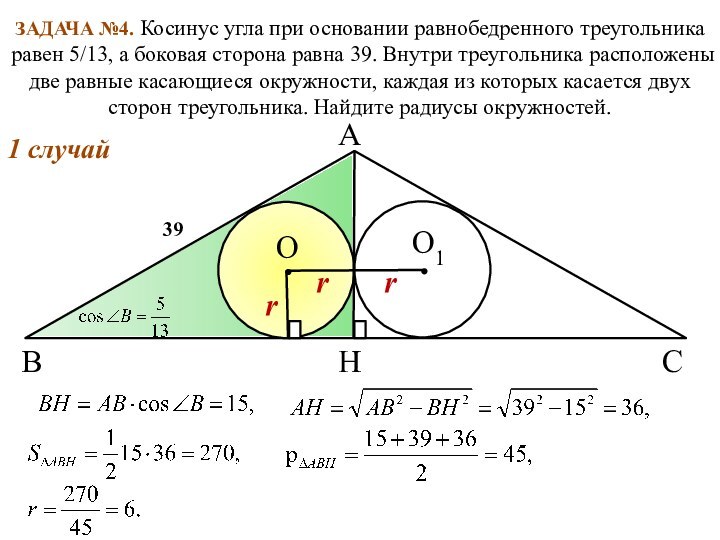
39

16. Косинус одного из углов равен -7/25. Две равные

окружности, касающиеся друг друга и двух сторон треугольника, вписаны в треугольник. Найти их радиусы.

Ответ:

в равнобедренный треугольник окружности делит его боковую сторону, если

известно, что радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон, в 7 раз больше радиуса вписанной окружности?

А

O

O1

D

K

r

a

b

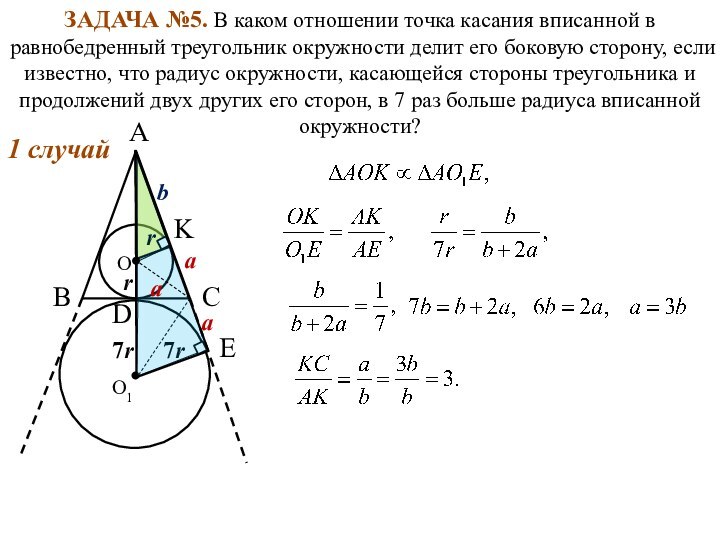
1 случай

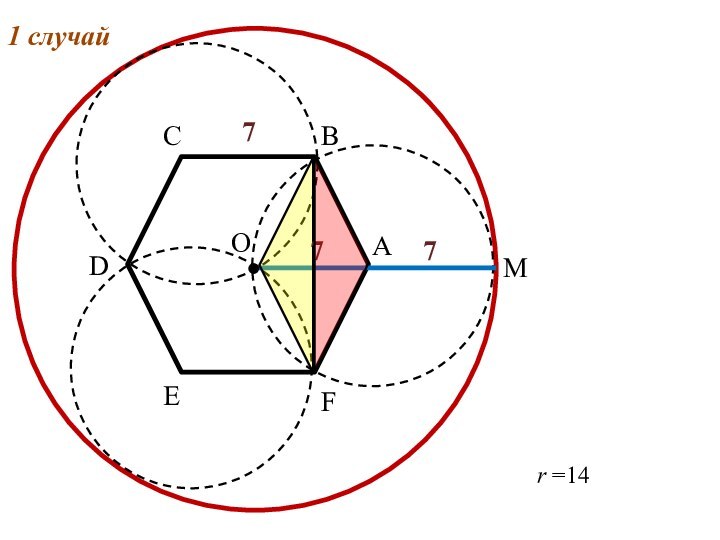
7r

7r

a

E

В

С

r

a

треугольник окружности делит его боковую сторону, если известно, что

отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других сторон, равно 2/7?

Дан равнобедренный треугольник. Найти угол при основании этого треугольника, если радиус вписанной окружности относится к радиусу окружности, касающейся одной из сторон и продолжений двух других сторон, как 1 : 4.


В каком отношении точка касания вписанной в равнобедренный треугольник окружности делит его боковую сторону, если известно, что отношение радиусов его вписанной окружности и окружности, касающейся стороны треугольника и продолжений двух других его сторон, равно 1/5?

Найдите косинус угла при основании равнобедренного треугольника, если известно, что радиус его вписанной окружности в 6 раз меньше радиуса окружности, касающейся стороны и продолжений двух других сторон треугольника.

Задачи для самостоятельного решения

Ответ:

Ответ:

Ответ:

Ответ:

KLMN равны 10 и 26 соответственно. Отрезок, соединяющий середины

диагоналей, равен 12, средняя линия трапеции равна 24. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.

K

L

C

N

10

26

A

12

E

F

M

D

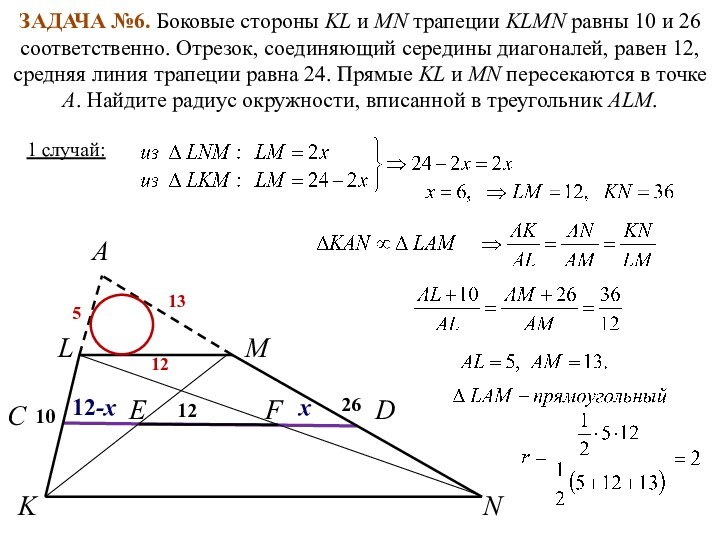
1 случай:

х

12-х

5

13

12

трапеции ABCD равны 6 и 8 соответственно. Отрезок, соединяющий

середины диагоналей, равен 5, средняя линия трапеции равна 25. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC.
Ответ: 4 или 6


Боковые стороны AB и CD трапеции ABCD равны 7 и 24 соответственно. Отрезок, соединяющий середины диагоналей, равен 12.5, средняя линия трапеции равна 27.5. Прямые AB и CD пересекаются в точке M. Найдите радиус окружности, вписанной в треугольник BMC.
Ответ: 1,8 или 4,8

прямой АС выбрана так, что треугольник АВЕ, площадь которого

равна 14, - равнобедренный с основанием АЕ и высотой BD. Найдите площадь треугольника АВС, если известно, что ∠ABE = ∠CBD = α и tg α = 24/7.

A

В

С

E

D

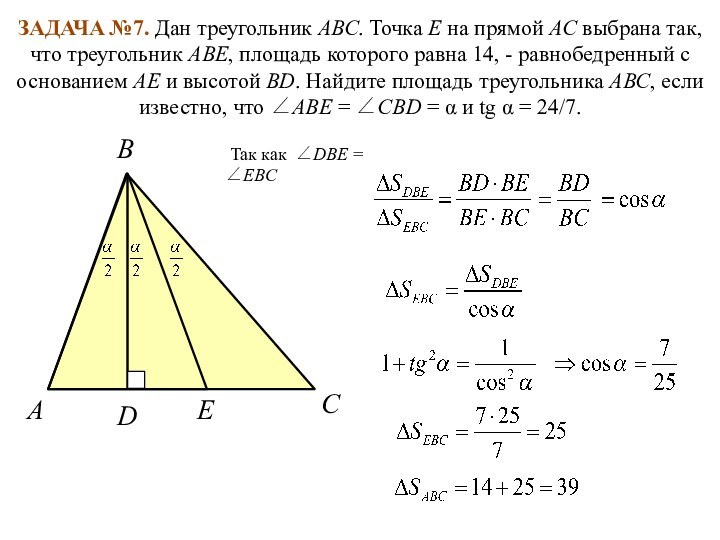
Так как ∠DBE = ∠EBC

или 39

равна 55. Точка Е на прямой АС выбрана так,

что треугольник АВЕ - равнобедренный с основанием АЕ и высотой BD. Найдите площадь треугольника АВE, если известно, что ∠ABE = ∠CBD =α и tgα = 4/3.
Ответ: 30 или 66

со стороной 7. Найдите радиус окружности, касающейся окружностей ,

описанных около треугольников BOD, DOF, BOF.

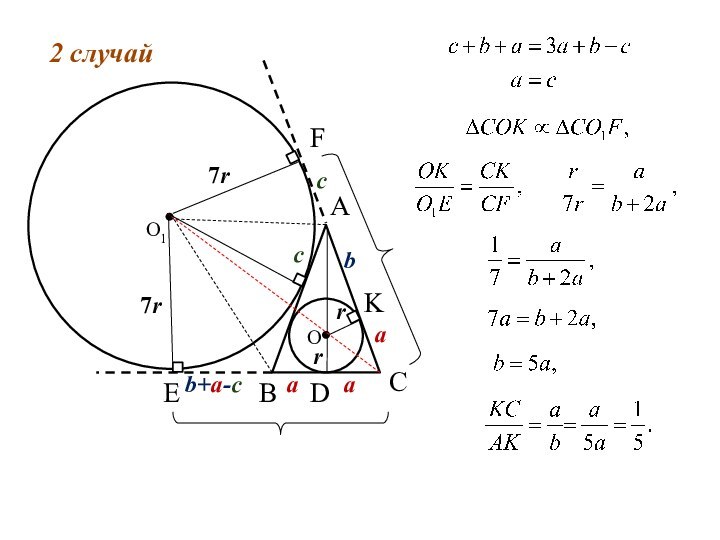
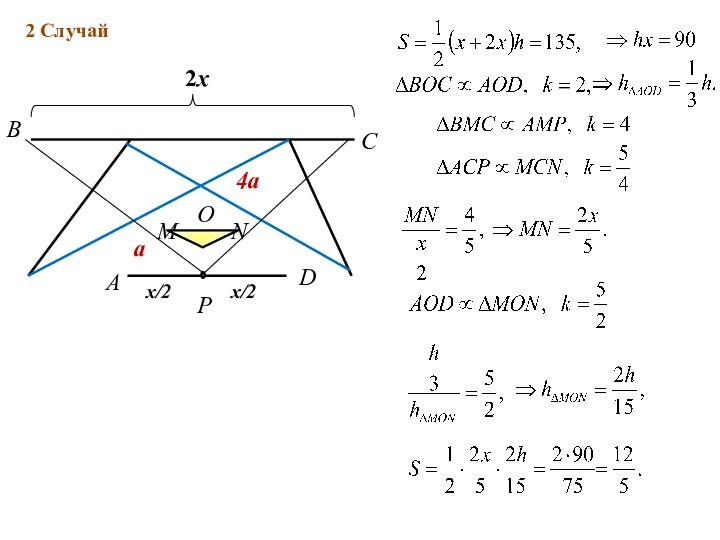
2 случай

1 случай

стороной . Найдите радиус окружности касающейся окружностей, описанных около

треугольников AOB, COD , EOF .

Задачa для самостоятельного решения

Ответ: 28 или 12

4 и углом 1200. Внутри него расположены две равные

касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

В

С

Н

О1

r

А

О

r

r

1 случай

4

600

пересекаются в точке O. Отрезки, соединяющие середину P основания

AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N . Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого.

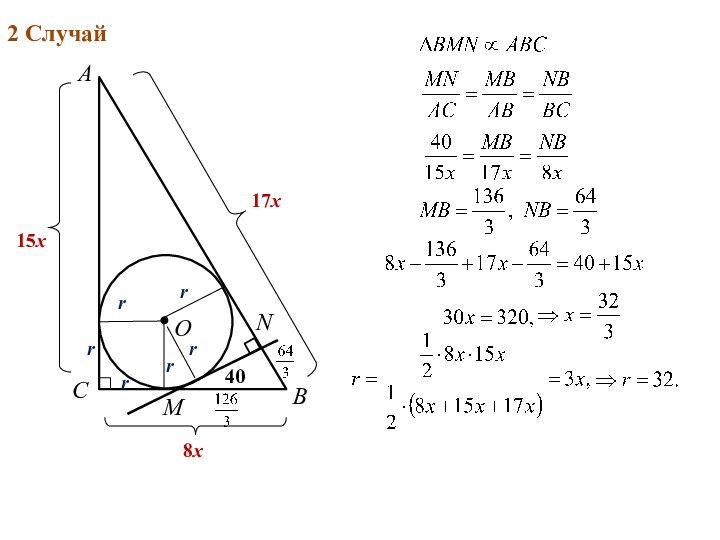
A

B

C

D

O

P

M

N

x

2x

x

x

a

2a

3a

M, N - середины диагоналей

ОС - медиана

1 Cлучай

Диагонали пересекаются в точке O. Отрезки, соединяющие середину P

основания AD с вершинами B и C, пересекаются с диагоналями трапеции в точках M и N. Найдите площадь треугольника MON, если одно из оснований трапеции вдвое больше другого.

Ответ: 22,5 или 14,4

проведена касательная параллельно основанию треугольника. Отрезок касательной между боковыми

сторонами равен 2. Найдите основание треугольника.

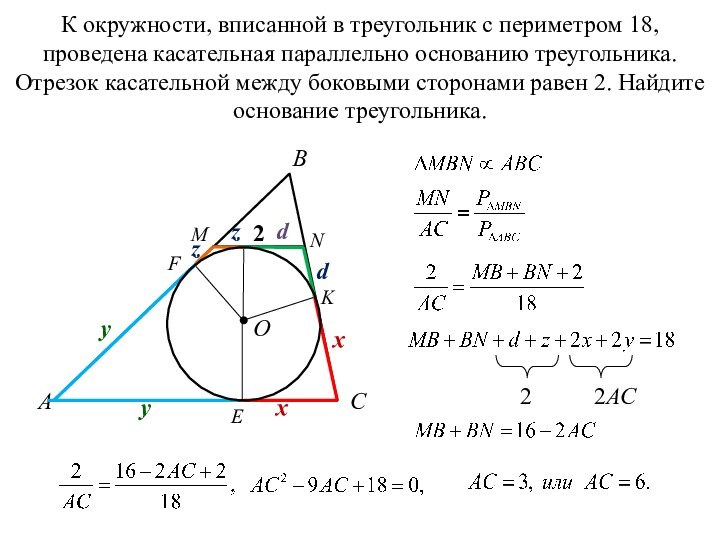
A

B

C

O

M

N

2

х

х

у

у

F

E

K

z

z

d

d

2

2AC

от него четырехугольник, в который можно вписать окружность. Найти

радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 40, а отношение катетов треугольника равно 15/8 .

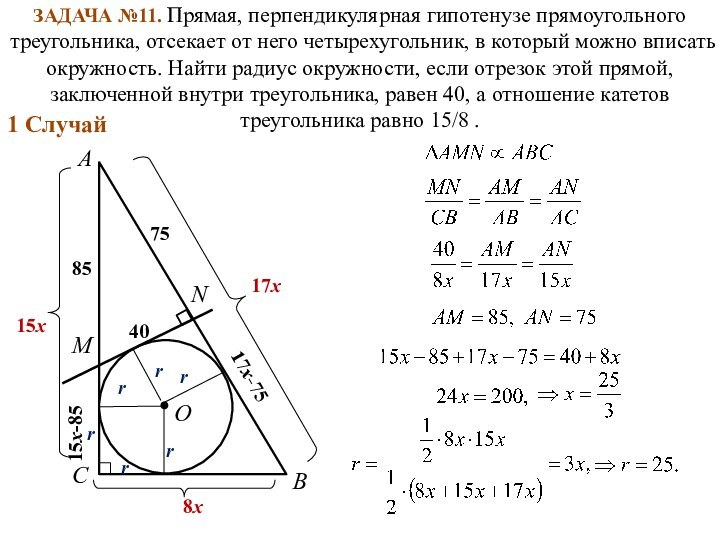
A

B

C

M

N

40

8x

15x

O

r

r

r

r

r

r

17x

75

85

17x-75

15x-85

1 Cлучай

отсекает от него четырехугольник, в который можно вписать окружность.

Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 10, а отношение катетов треугольника равно 5/12 .


Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 6, а отношение катетов треугольника равно 3/4 .


Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь четырехугольника, если гипотенуза треугольника равна 10, а радиус окружности, равен 2 .

Ответ:

Ответ:

Ответ:

отсекает от него четырехугольник, в который можно вписать окружность.

Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 12, а косинус острого угла равен 0,6 .


Прямая, перпендикулярная боковой стороне равнобедренного треугольника с основанием равным 12, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь четырехугольника, если радиус окружности равен 3.


Прямая, перпендикулярная боковой стороне равнобедренного треугольника , отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 24, а синус угла при основании равен 0,8 .

Ответ:

Ответ:

Ответ:

с катетами 6 и 8, отсекает от него четырехугольник,

в который можно вписать окружность. Найти площадь этого четырехугольника.

Прямая, перпендикулярная гипотенузе прямоугольного треугольника с катетами 5 и 12, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь этого четырехугольника.


Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 20, а отношение боковой стороны треугольника к его основанию равно 13/10 .


Прямая, перпендикулярная боковой стороне равнобедренного треугольника, отсекает от него четырехугольник, в который можно вписать окружность. Найти радиус окружности, если отрезок этой прямой, заключенной внутри треугольника, равен 6, а отношение боковой стороны треугольника к его основанию равно 5/6.

Ответ:

Ответ:

Ответ:

Ответ:

Ответ:

равным и 10, 10, 12, отсекает от него четырехугольник,

в который можно вписать окружность. Найти площадь четырехугольника.


Прямая, перпендикулярная боковой стороне равнобедренного треугольника со сторонами равным и 10, 13, 13, отсекает от него четырехугольник, в который можно вписать окружность. Найти площадь четырехугольника.

Задачи для самостоятельного решения.

Ответ:

Ответ:

На окружности с диаметром АВ взята точка С, удаленная

от точек А, М и В на расстояния 40, 29 и 30 соответственно. Найти площадь треугольника ВМС.

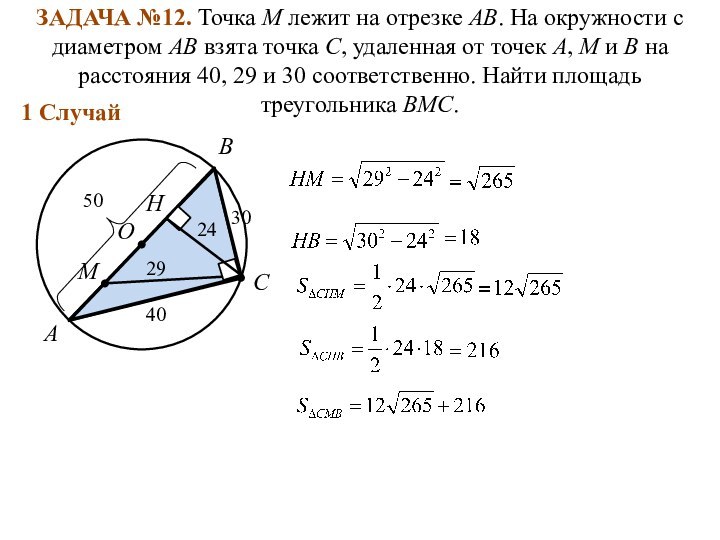
A

B

O

M

40

29

30

C

50

24

H

1 Cлучай