ЗАНЯТИЯ:
Переход от дифференциальных уравнений к структурным схемам
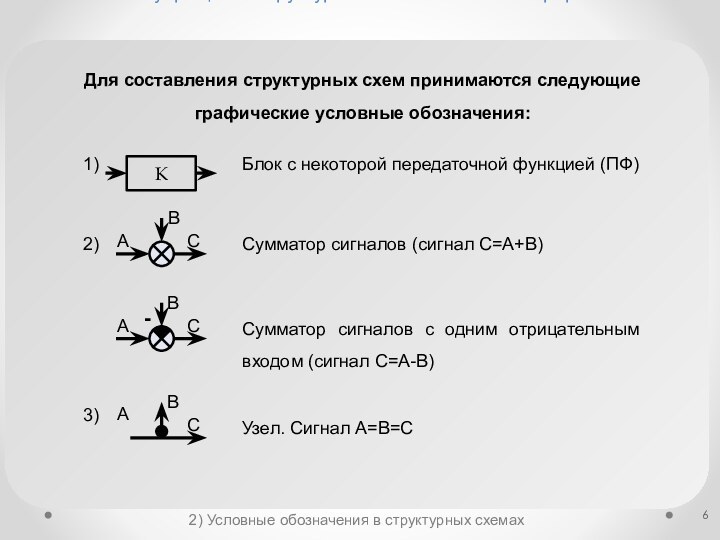
Условные обозначения в
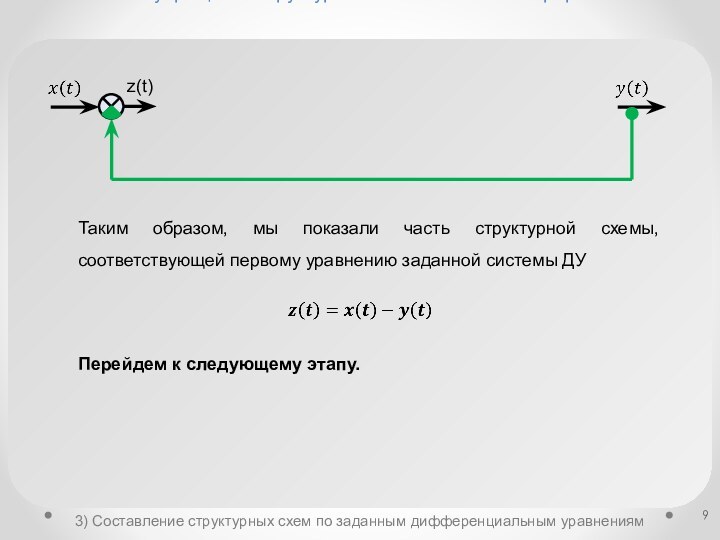
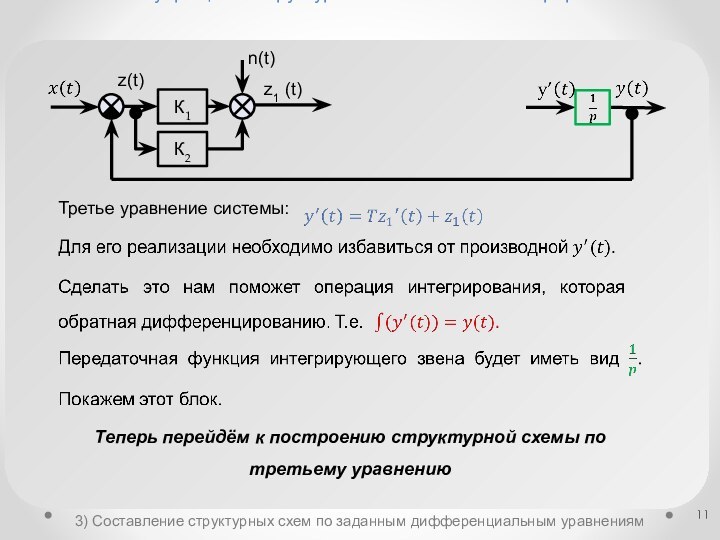
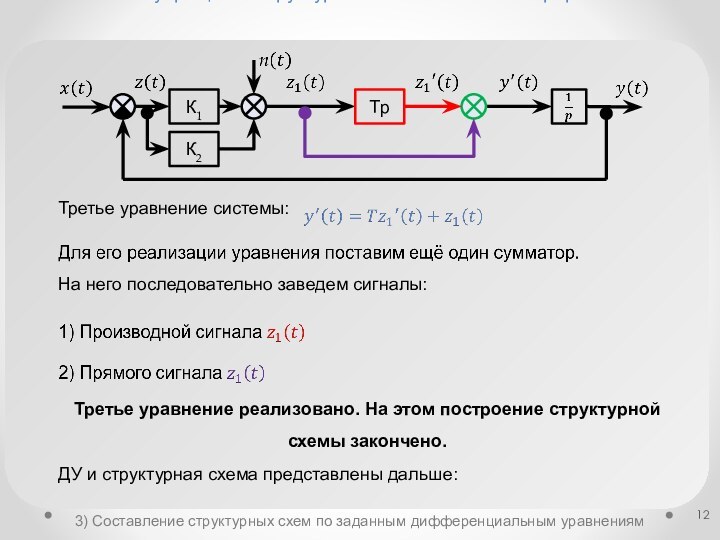
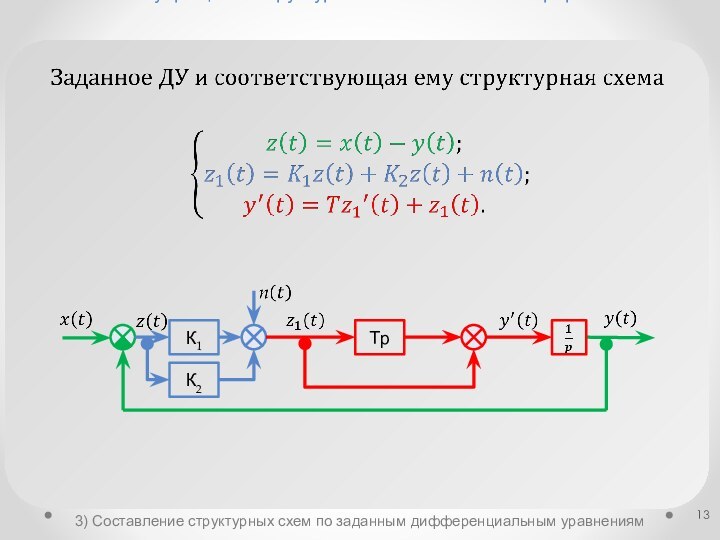
структурных схемахСоставление структурных схем по заданным дифференциальным уравнениям
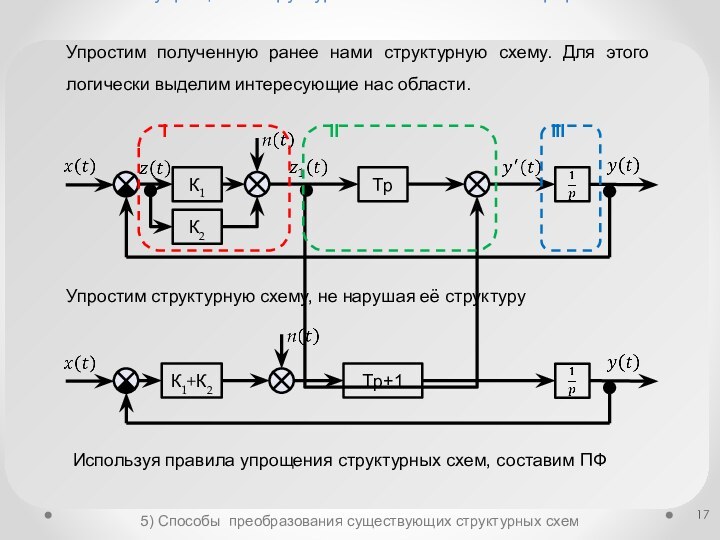
Правила упрощения структурных схем
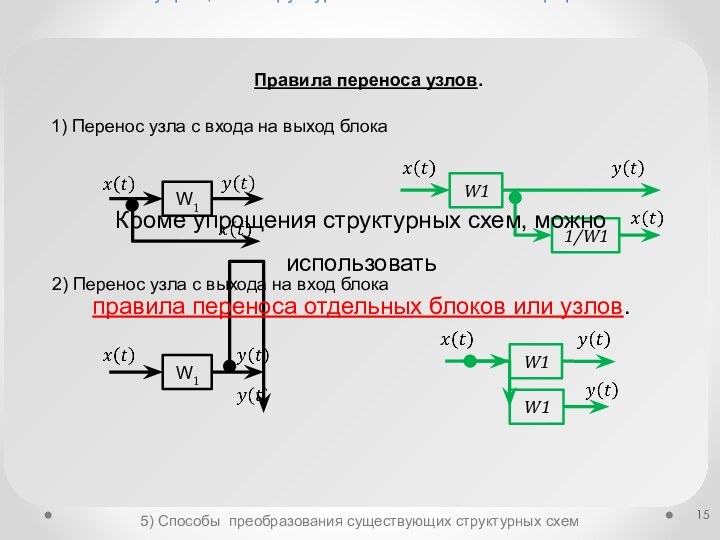
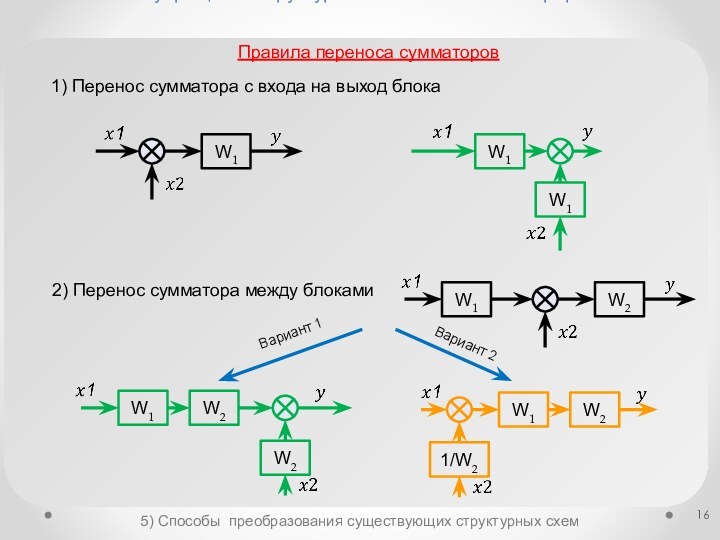
Способы преобразования существующих структурных схем
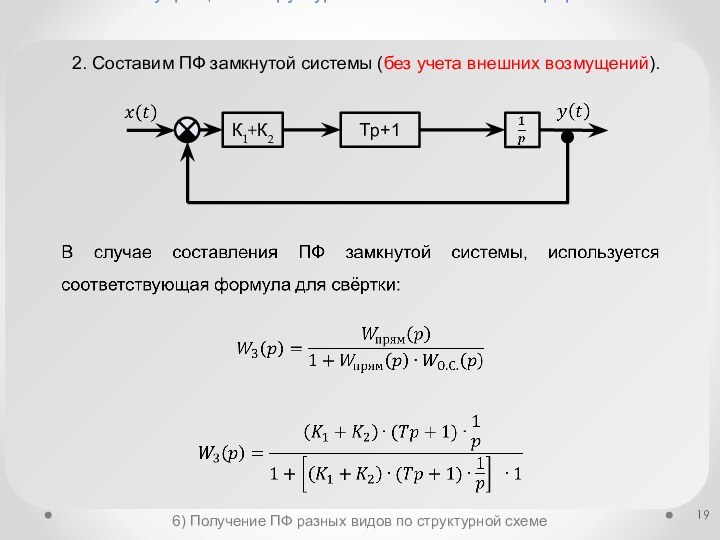
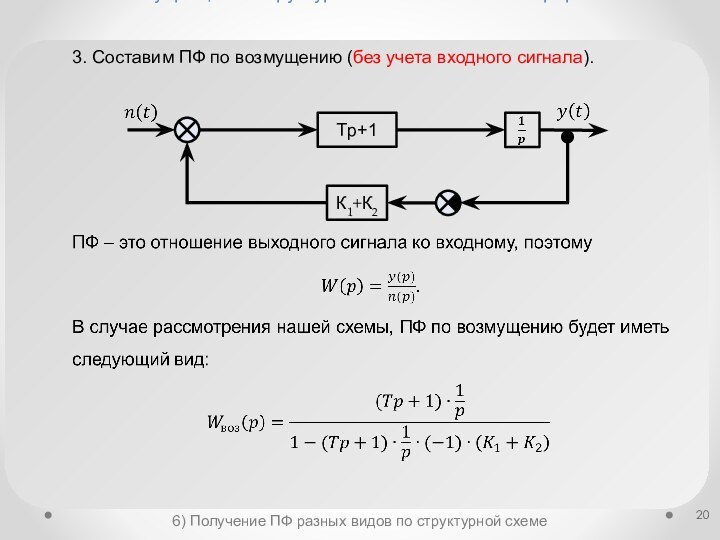
Получение ПФ разных видов по структурной схеме
Выводы по изложенному материалу