- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тема 1. Введение в теорию сигналов и систем
Содержание
- 2. 1.1. Общие сведения и понятияПонятие сигнала.В технических
- 3. Термин “сигнал” часто отождествляют с понятиями “данные”
- 4. Термин "signal" в мировой практике является общепринятым
- 5. Наиболее распространенное представление сигналов - в электрической
- 6. С математической точки зрения сигнал представляет собой
- 7. Под "анализом" сигналов имеется в виду не
- 8. С понятием сигнала неразрывно связан термин регистрации
- 9. Шумы и помехи. При детектировании сигналов, несущих
- 10. Виды шумов и помех разделяют по источникам
- 11. Помехи подразделяются на флюктуационные, импульсные и периодические.
- 12. В зависимости от характера воздействия на сигнал
- 13. Размерность сигналов.Простейшими сигналами являются одномерные сигналы. Значения
- 14. Математическое описание сигналов.Сигналы могут быть объектами теоретических
- 15. Спектральное представление сигналов. Кроме динамического представления сигналов
- 16. Кроме гармонического ряда Фурье применяются и другие
- 17. Математические модели сигналов. Теория анализа и обработки
- 18. Знание математических моделей сигналов дает возможность классифицировать
- 19. Неотъемлемой частью любой математической модели сигнала является
- 20. Виды моделей сигналов. При анализе физических данных
- 21. Второй подход предполагает случайный характер сигналов, закон
- 22. Классификация сигналов осуществляется на основании существенных признаков
- 23. С математических позиций группы сигналов обычно называют
- 24. Классификация детерминированных сигналов.Обычно выделяют два класса детерминированных
- 25. Гармонические сигналы (синусоидальные), описываются следующими формулами:s(t) =
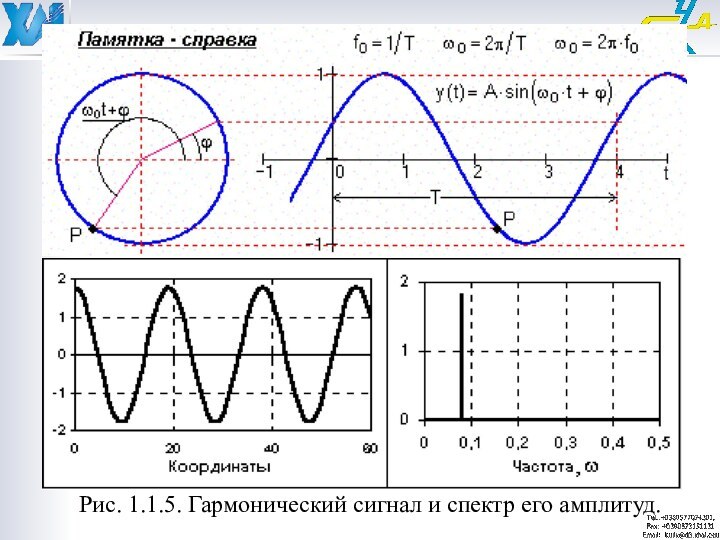
- 26. Рис. 1.1.5. Гармонический сигнал и спектр его амплитуд.
- 27. Полигармонические сигналы составляют наиболее широко распространенную группу
- 29. Информационными параметрами полигармонического сигнала могут быть как
- 30. К непериодическим сигналам относят почти периодические и
- 31. Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени.
- 32. К апериодическим сигналам относятся также импульсные сигналы,
- 33. Скачать презентацию
- 34. Похожие презентации
1.1. Общие сведения и понятияПонятие сигнала.В технических отраслях знаний термин "сигнал" (signal, от латинского signum – знак) используется в широком смысловом диапазоне. Под ним понимают и техническое средство для передачи, обращения и использования информации - электрический,
























Слайд 3
Термин “сигнал” часто отождествляют с понятиями “данные” (data)
и “информация” (information). Действительно, эти понятия взаимосвязаны, но относятся
к разным категориям.Понятие информации имеет много определений, от наиболее широкого (информация есть формализованное отражение реального мира) до практического (сведения, являющиеся объектом хранения, передачи, преобразования, восприятия и управления). Что касается “данных” (от латинского datum – факт), то это совокупность фактов, результатов наблюдений, измерения каких-либо физических свойств объектов, явлений или процессов материального мира, представленных в формализованном виде. Это не информация, а сырье для получения информации путем соответствующей обработки и интерпретации (истолкования).
Слайд 4
Термин "signal" в мировой практике является общепринятым для
характеристики формы представления данных, при которой данные рассматриваются как
результат некоторых измерений объекта исследований в виде последовательности значений скалярных величин (аналоговых, числовых, графических и пр.) в зависимости от изменения каких-либо переменных значений (времени, энергии, температуры, пространственных координат, и пр.). А так как данные содержат информацию, как об основных целевых параметрах объекта исследований, так и о различных сопутствующих и мешающих факторах измерений, то в широком смысле этого слова можно считать, что сигнал является носителем общей измерительной информации. При этом материальная форма носителей сигналов (механическая, электрическая, магнитная, акустическая, оптическая и любая другая), равно как и форма отображения данных в каких-либо физических параметрах или процессах носителей, значения не имеет. Информативным параметром сигнала может являться любой параметр носителя сигнала, функционально и однозначно связанный со значениями информационных данных.
Слайд 5
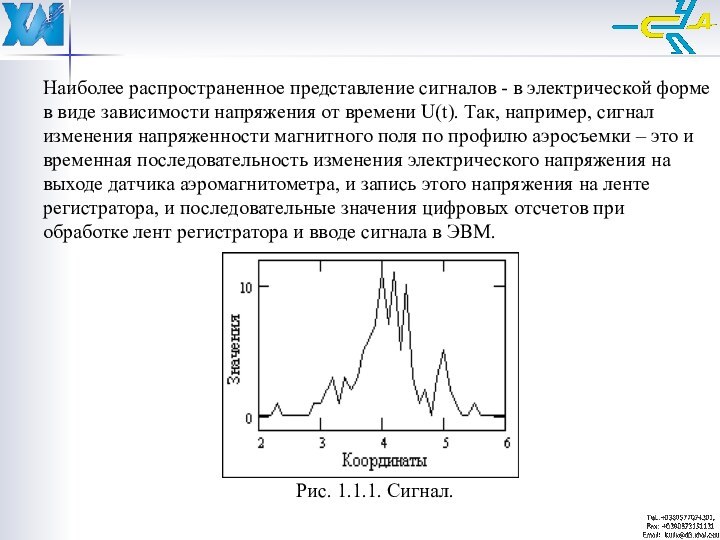
Наиболее распространенное представление сигналов - в электрической форме
в виде зависимости напряжения от времени U(t). Так, например,
сигнал изменения напряженности магнитного поля по профилю аэросъемки – это и временная последовательность изменения электрического напряжения на выходе датчика аэромагнитометра, и запись этого напряжения на ленте регистратора, и последовательные значения цифровых отсчетов при обработке лент регистратора и вводе сигнала в ЭВМ.Рис. 1.1.1. Сигнал.
Слайд 6
С математической точки зрения сигнал представляет собой функцию,
т.е. зависимость одной величины от другой, независимой переменной. По
содержанию это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды. А целью обработки сигналов можно считать извлечение определенных информационных сведений, которые отображены в этих сигналах (кратко - полезная или целевая информация) и преобразование этих сведений в форму, удобную для восприятия и дальнейшего использования.
Слайд 7
Под "анализом" сигналов имеется в виду не только
их чисто математические преобразования, но и получение на основе
этих преобразований выводов о специфических особенностях соответствующих процессов и объектов. Целями анализа сигналов обычно являются:- Определение или оценка числовых параметров сигналов (энергия, средняя мощность, среднее квадратическое значение и пр.).
- Изучение изменения параметров сигналов во времени.
- Разложение сигналов на элементарные составляющие для сравнения свойств различных сигналов.
- Сравнение степени близости, "похожести", "родственности" различных сигналов, в том числе с определенными количественными оценками.
Слайд 8
С понятием сигнала неразрывно связан термин регистрации сигналов,
использование которого также широко и неоднозначно, как и самого
термина сигнал. В наиболее общем смысле под этим термином можно понимать операцию выделения сигнала и его преобразования в форму, удобную для дальнейшего использования. Так, при получении информации о физических свойствах каких-либо объектов, под регистрацией сигнала понимают процесс измерения физических свойств объекта и перенос результатов измерения на материальный носитель сигнала или непосредственное энергетическое преобразование каких-либо свойств объекта в информационные параметры материального носителя сигнала (как правило - электрического). Но так же широко термин регистрации сигналов используют и для процессов выделения уже сформированных сигналов, несущих определенную информацию, из суммы других сигналов (радиосвязь, телеметрия и пр.), и для процессов фиксирования сигналов на носителях долговременной памяти, и для многих других процессов, связанных с обработкой сигналов.
Слайд 9
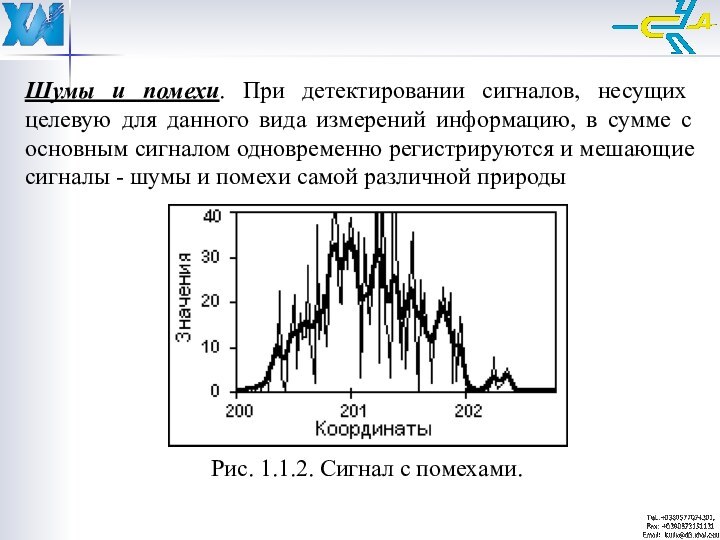
Шумы и помехи. При детектировании сигналов, несущих целевую
для данного вида измерений информацию, в сумме с основным
сигналом одновременно регистрируются и мешающие сигналы - шумы и помехи самой различной природыРис. 1.1.2. Сигнал с помехами.
Слайд 10
Виды шумов и помех разделяют по источникам их
возникновения, по энергетическому спектру, по характеру воздействия на сигнал,
по вероятностным характеристикам и другим признакам. Источники шумов и помех бывают внутренние и внешние.Внутренние, как правило, присущи физической природе источников и детекторов сигналов, а также их материальных носителей. Например, флюктуации интенсивности излучения радионуклидов в силу статистической природы ядерных процессов, тепловые шумы электронных потоков в электрических цепях, и т.п.
Внешние источники шумов и помех бывают искусственного и естественного происхождения. К искусственным источникам относятся индустриальные помехи и помехи от работающей физико-технической аппаратуры. Естественными источниками являются молнии, флюктуации магнитных полей, всплески солнечной энергии, и т.д.
Слайд 11
Помехи подразделяются на флюктуационные, импульсные и периодические.
Флюктуационные
помехи представляют собой хаотические и беспорядочные во времени процессы
в виде нерегулярных случайных всплесков различной амплитуды. Как правило, флюктуационные помехи распределены по нормальному закону с нулевым средним.Импульсные помехи проявляются как в виде отдельных импульсов, так и в виде последовательности импульсов, форма и параметры которых имеют случайный характер. Причинами импульсных помех являются резкие броски тока и напряжения в промышленных установках, транспортных средствах, а также природные электрические явления.
Периодические помехи вызываются электромагнитными полями линий электропередач, силовых электроустановок и др. Если основная мощность помех сосредоточена на отдельных участках диапазона частот, например, на частоте напряжения промышленной сети или кратна этой частоте, то такие помехи называют сосредоточенными.
Слайд 12
В зависимости от характера воздействия на сигнал помехи
разделяют на аддитивные и мультипликативные. Аддитивные (налагающиеся) помехи суммируются
с сигналом, не зависят от его значений и формы и не изменяют информативной составляющей самого сигнала. Мультипликативные или деформирующие помехи могут изменять форму информационной части сигнала, иметь зависимость от его значений и от определенных особенностей в сигнале и т.п. При известном характере мультипликативных помех возможна коррекция сигнала на их влияние. Следует заметить, что деление сигналов на полезные и мешающие (шумовые) является достаточно условным. Источниками мешающих сигналов также могут быть определенные физические процессы, явления или объекты. При выяснении природы мешающих сигналов они могут переводиться в разряд информационных.
Слайд 13
Размерность сигналов.
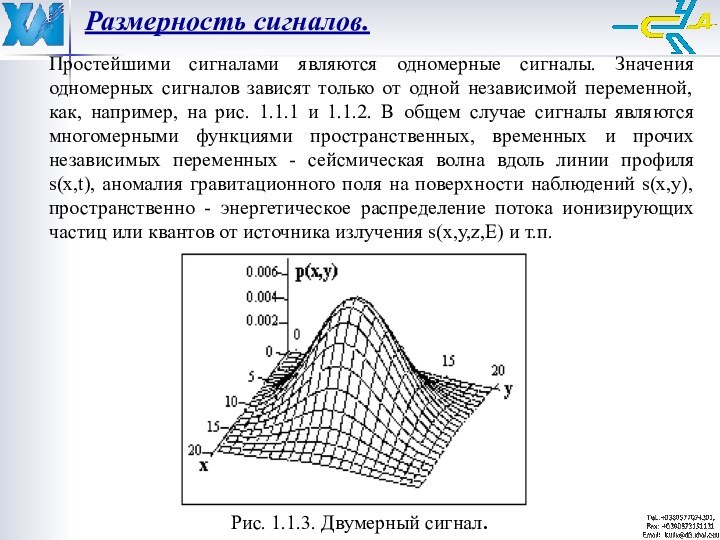
Простейшими сигналами являются одномерные сигналы. Значения одномерных
сигналов зависят только от одной независимой переменной, как, например,
на рис. 1.1.1 и 1.1.2. В общем случае сигналы являются многомерными функциями пространственных, временных и прочих независимых переменных - сейсмическая волна вдоль линии профиля s(x,t), аномалия гравитационного поля на поверхности наблюдений s(x,y), пространственно - энергетическое распределение потока ионизирующих частиц или квантов от источника излучения s(x,y,z,Е) и т.п.Рис. 1.1.3. Двумерный сигнал.
Слайд 14
Математическое описание сигналов.
Сигналы могут быть объектами теоретических исследований
и практического анализа только в том случае, если указан
способ их математического описания. Математическое описание позволяет абстрагироваться от физической природы сигнала и материальной формы его носителя, проводить классификацию сигналов, выполнять их сравнение, устанавливать степень тождества, моделировать системы обработки сигналов.Большинство сигналов, встречающихся на практике, представлены во временной области функциями времени. При отображении сигналов на графике одной из координат (независимой) является ось времени, а другой координатой (зависимой) – ось амплитуд. Тем самым мы получаем амплитудно-временное представление сигнала. В общем случае описание сигнала задается функциональной зависимостью определенного информационного параметра сигнала от независимой переменной (аргумента) – s(х), y(t) и т.п. Такая форма описания и графического представления сигналов называется динамической (сигнал в реальной динамике его поведения по аргументам). Функции математического описания сигналов могут быть как вещественными, так и комплексными. Выбор математического аппарата описания определяется простотой и удобством его использования при анализе и обработке сигналов.
Слайд 15
Спектральное представление сигналов.
Кроме динамического представления сигналов и
функций в виде зависимости их значений от определенных аргументов
при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой сколь угодно сложный по своей форме сигнал, не имеющий разрывов второго рода (бесконечных значений на интервале своего задания), можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, что выполняется при помощи преобразования Фурье. Соответственно, математически разложение сигнала на гармонические составляющие описывается функциями значений амплитуд и начальных фаз колебаний по непрерывному или дискретному аргументу – частоте изменения функций на определенных интервалах аргументов их динамического представления. Совокупность амплитуд гармонических колебаний разложения называют амплитудным спектром сигнала, а совокупность начальных фаз – фазовым спектром. Оба спектра вместе образуют полный частотный спектр сигнала, который по точности математического представления тождественен динамической форме описания сигнала.
Слайд 16
Кроме гармонического ряда Фурье применяются и другие виды
разложения сигналов: по функциям Уолша, Бесселя, Хаара, полиномам Чебышева,
и др. Главное условие однозначности и математической идентичности отображения сигналов - ортогональность функций разложения. При качественном анализе сигналов могут применяться и неортогональные функции, выявляющие какие-либо характерные особенности сигналов, полезные для интерпретации физических данных.
Слайд 17
Математические модели сигналов.
Теория анализа и обработки физических
данных базируется на математических моделях соответствующих физических полей и
физических процессов, на основе которых создаются математические модели сигналов. Математические модели сигналов дают возможность обобщенно, абстрагируясь от физической природы, судить о свойствах сигналов, предсказывать изменения сигналов в изменяющихся условиях, заменять физическое моделирование процессов математическим. С помощью математических моделей имеется возможность описывать свойства сигналов, которые являются главными в изучаемых процессах, и игнорировать большое число второстепенных признаков.
Слайд 18
Знание математических моделей сигналов дает возможность классифицировать их
по различным признакам, характерным для того или иного типа
моделей. Так, сигналы разделяются на неслучайные и случайные в зависимости от возможности точного предсказания их значений в любые моменты времени. Сигнал является неслучайным и называется детерминированным, если математическая модель позволяет осуществлять такое предсказание. Детерминированный сигнал задается, как правило, математической функцией или вычислительным алгоритмом, а математическая модель сигнала может быть представлена в видеs = F(t, z, ω,…; A, B, C,…),
где s – информативный параметр сигнала; t, z, w, … – независимые аргументы (время, пространственная координата, частота и др.); A, B, C… – параметры сигналов.
Модель должна быть, по возможности, проще, минимизирована по количеству независимых аргументов и адекватна изучаемому процессу.
Слайд 19
Неотъемлемой частью любой математической модели сигнала является область
определения сигнала, которая устанавливается интервалом задания независимой переменной. Примеры
задания интервала для переменных:a ≤ x ≤ b, x ∈ [a, b].
a < y ≤ b, y ∈ (a, b].
a < z < b, z ∈ (a, b).
Математические модели полей и сигналов на первом этапе обработки и анализа результатов наблюдений должны позволять в какой-то мере игнорировать их физическую природу и возвращать ее в модель только на заключительном этапе интерпретации данных.
Слайд 20
Виды моделей сигналов.
При анализе физических данных используются
два основных подхода к созданию математических моделей сигналов.
Первый подход
оперирует с детерминированными сигналами, значения которых в любой момент времени или в произвольной точке пространства (а равно и в зависимости от любых других аргументов) являются априорно известными или могут быть определены (вычислены) с определенной степенью точности. Такой подход удобен в прямых задачах геофизики (расчеты полей для заданных моделей сред), в задачах активных воздействий на среду при заранее известных параметрах и форме сигнала воздействия (вибрационная сейсморазведка, электромагнитные методы каротажа и пр.), а также при использовании хорошо известных геолого-геофизических данных.
Слайд 21
Второй подход предполагает случайный характер сигналов, закон изменения
которых во времени (или в пространстве) носит случайный характер,
и которые принимают конкретные значения с некоторой вероятностью. Модель такого сигнала представляет собой описание статистических характеристик случайного процесса путем задания закона распределения вероятностей, корреляционной функции, спектральной плотности энергии и др.Между этими двумя видами сигналов нет резкой границы. Строго говоря, детерминированных процессов и отвечающих им детерминированных сигналов в природе не существует.
С другой стороны, модель случайного поля часто аппроксимируется методом суперпозиции сигналов известной формы. Детерминированные модели могут использоваться и для изучения случайных процессов, если уровень полезного сигнала в этом процессе значительно выше уровня статистических флюктуаций.
Слайд 22
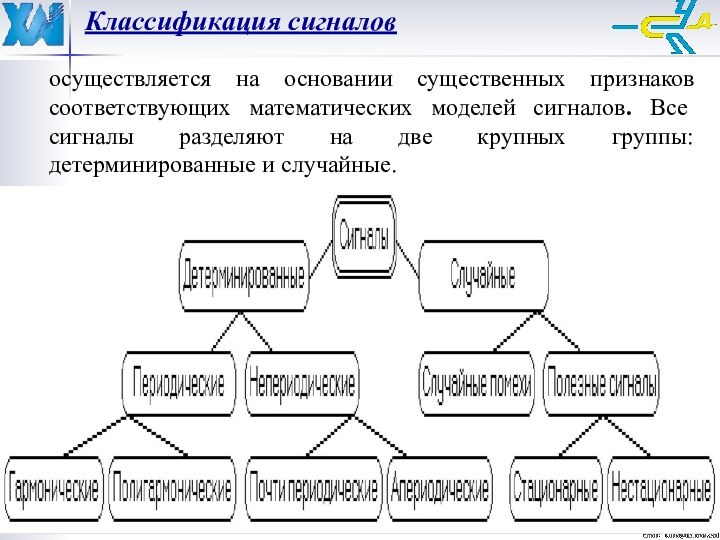
Классификация сигналов
осуществляется на основании существенных признаков соответствующих
математических моделей сигналов. Все сигналы разделяют на две крупных
группы: детерминированные и случайные.
Слайд 23
С математических позиций группы сигналов обычно называют множествами,
в которые объединяют сигналы по какому-либо общему свойству. Принадлежность
сигнала s к множеству LР записывается в виде LP = {s; P}, где Р – определенное свойство данного множества сигналов.
Слайд 24
Классификация детерминированных сигналов.
Обычно выделяют два класса детерминированных сигналов:
периодические и непериодические.
К множеству периодических относят гармонические и полигармонические
сигналы. Для периодических сигналов выполняется общее условие s(t) = s(t + kT), где k = 1, 2, 3, ... - любое целое число (из множества целых чисел I от -∞ до ∞), Т - период, являющийся конечным отрезком независимой переменной. Множество периодических сигналов:LP = {s(t); s(t+kT) = s(t), -∞ < t < ∞, k∈I}.
Слайд 25
Гармонические сигналы (синусоидальные), описываются следующими формулами:
s(t) = A⋅sin
(2πfоt+φ) = A⋅sin (ωоt+φ), s(t) = A⋅cos(ωоt+ϕ), (1.1.1)
где А,
fo, ωo, ϕ, φ - постоянные величины, которые могут исполнять роль информационных параметров сигнала: А - амплитуда сигнала, fо - циклическая частота в герцах, ωо = 2πfо - угловая частота в радианах, ϕ и φ- начальные фазовые углы в радианах.Период одного колебания T = 1/fо = 2π/ωo. При ϕ = φ-π/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты fо (при t = 0).
Слайд 27
Полигармонические сигналы составляют наиболее широко распространенную группу периодических
сигналов и описываются суммой гармонических колебаний:
s(t) =An sin (2πfnt+ϕn)
≡ An sin (2πBnfpt+ϕn), Bn ∈ I, (1.1.2)или непосредственно функцией s(t) = y(t ± kTp), k = 1,2,3,..., где Тр - период одного полного колебания сигнала y(t), заданного на одном периоде. Значение fp =1/Tp называют фундаментальной частотой колебаний.
Слайд 29
Информационными параметрами полигармонического сигнала могут быть как определенные
особенности формы сигнала (размах от минимума до максимума, экстремальное
отклонение от среднего значения, и т.п.), так и параметры определенных гармоник в этом сигнале. Так, например, для прямоугольных импульсов информационными параметрами могут быть период повторения импульсов, длительность импульсов, скважность импульсов (отношение периода к длительности). При анализе сложных периодических сигналов информационными параметрами могут также быть:- Текущее среднее значение за определенное время, например, за время периода: (1/Т)s(t) dt.
- Постоянная составляющая одного периода: (1/Т)s(t) dt.
- Среднее выпрямленное значение: (1/Т)|s(t)| dt.
- Среднее квадратичное значение:
Слайд 30
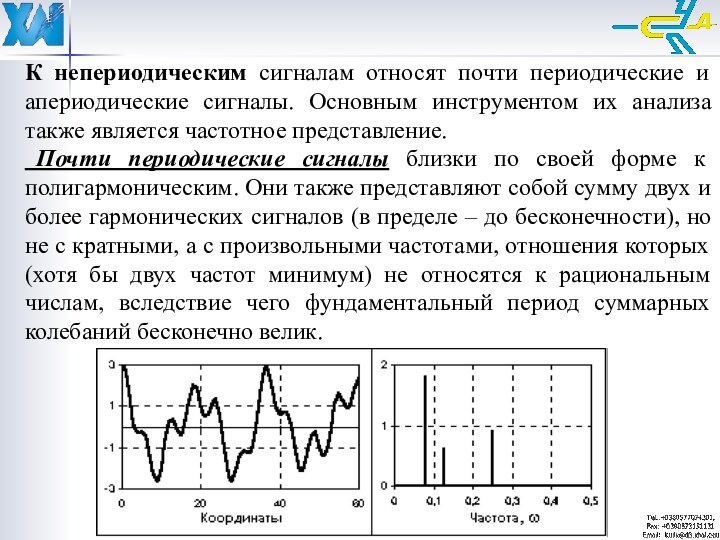
К непериодическим сигналам относят почти периодические и апериодические
сигналы. Основным инструментом их анализа также является частотное представление.
Почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов (в пределе – до бесконечности), но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик.
Слайд 31
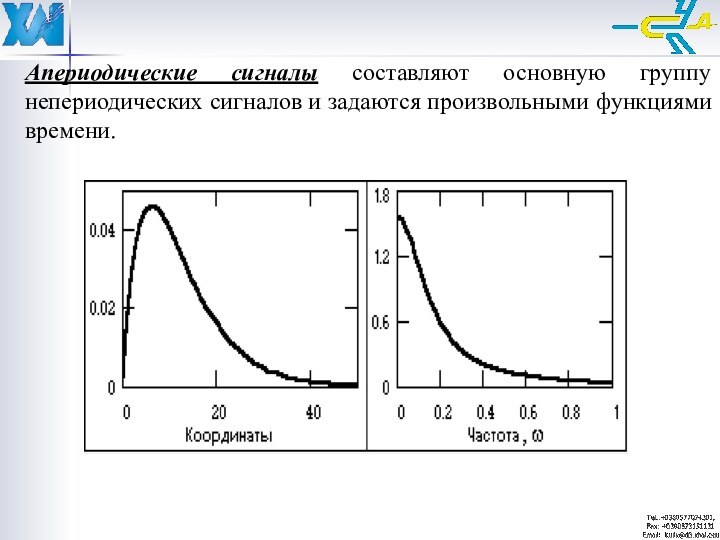
Апериодические сигналы составляют основную группу непериодических сигналов и
задаются произвольными функциями времени.
Слайд 32
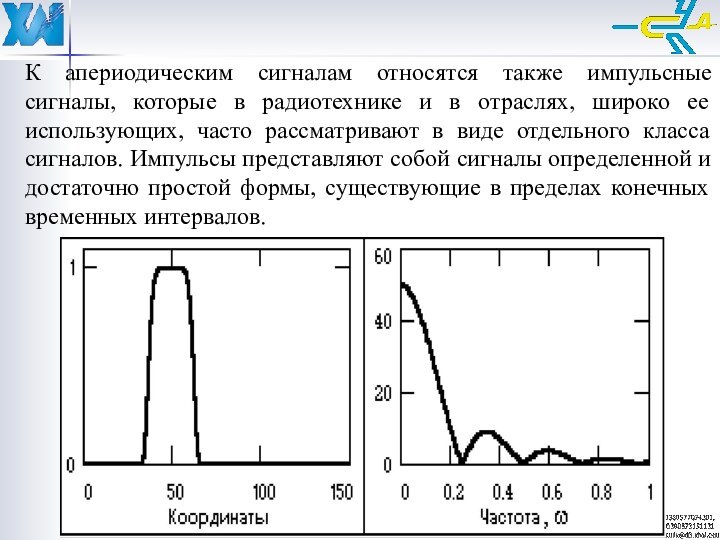
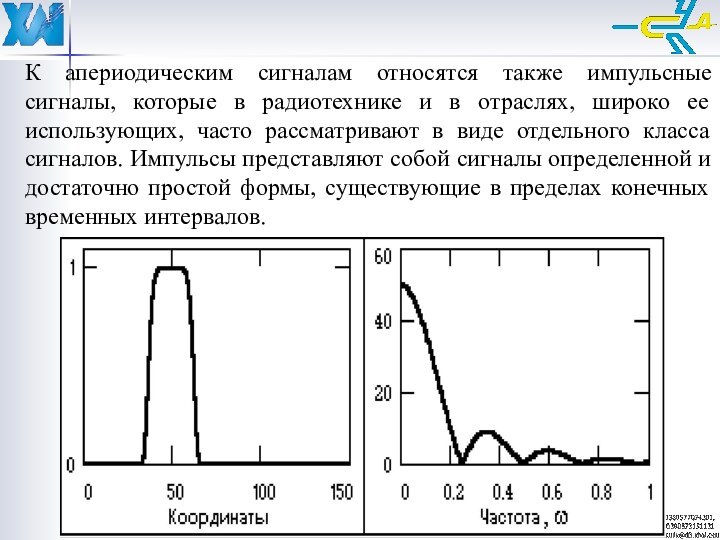
К апериодическим сигналам относятся также импульсные сигналы, которые
в радиотехнике и в отраслях, широко ее использующих, часто
рассматривают в виде отдельного класса сигналов. Импульсы представляют собой сигналы определенной и достаточно простой формы, существующие в пределах конечных временных интервалов.