Слайд 2
Цель изучения дисциплины
Расчеты пути на прочность и устойчивость
сводятся к определению напряжений и деформаций в его элементах
под нагрузкой.
Результаты расчетов пути могут использоваться в целях:
оценки напряженно-деформированного состояния данной конструкции пути при заданных условиях эксплуатации;
определения таких нагрузок и скоростей движения поездов, при которых напряжения и деформации, возникающие в пути, не будут превосходить допустимых, а его устойчивость будет надежно обеспечена;
проектирования новых конструкций пути.
Слайд 3
Работу оформить в соответствии со стандартом организации СТО
СГУПС 1.01С.02-2006 «Курсовой и дипломный проекты. Требования к оформлению».
Список
используемой литературы приведен на бланке с заданием.
Для формул выполнять сквозную нумерацию (1), (2), (3)… или с указанием раздела (1.1), (1.2), (1.3)…. Аналогично для рисунков.
Слайд 5
Все физико-механические характеристики пути принимаются детерминированными (неслучайными, постоянными
для заданных условий).
Расчет ведется на вертикальные силы, приложенные к
оси симметрии рельса. Действие горизонтальных сил учитываются коэффициентом.
Напряжения и деформации в расчетных сечениях вычисляются как алгебраические суммы этих величин от действия различных нагрузок (принцип независимости действия сил).
Слайд 10
Параметры типовых поперечных профилей балластной призмы
В числителе приведены
значения для звеньевого пути при деревян-ных шпалах; в знаменателе
- для бесстыкового пути на железобетон-ных шпалах.
Слайд 11
Поперечный профиль балластной призмы
Чертеж изображается на листе пояснительной
записки (построенный в графическом редакторе) или листе миллиметровой бумаги
формата А4 (чертится карандашом), расположенный в альбомной ориентации (горизонтальном положении). Масштаб чертежа 1:50. На чертеже указать размеры. Длина железобетонной шпалы 2,7 м.
Рисунок 2 – Поперечный профиль балластной призмы
Слайд 14
добавок
где qк – вес необрессоренной части экипажа, приходящийся
на одно колесо, Н;
kд – коэффициент динамических добавок от
вертикальных колебаний надрессорной части, определяемый по эмпирической зависимости
где v – скорость движения, м/с;
fст – статический прогиб рессорного подвешивания, м.
Среднеквадратическое отклонение динамической нагрузки колеса на рельс S от нескольких факторов определяется из суммы дисперсий, Н
Слайд 15
где Sp – среднеквадратическое отклонение динамической нагрузки колеса
на рельс от вертикальных колебаний надрессорной части экипажа, Н;
Sнп
– среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренным масс при прохождении колесом изолированной неровности пути, Н;
Sннк – среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренным масс из-за наличия непрерывных неровностей на поверхности катания колес, Н;
Sинк – среднеквадратическое отклонение динамической нагрузки колеса на рельс от действия сил инерции необрессоренным масс, возникающих из-за наличия изолированных неровностей на поверхности катания колес, Н;
q1 – доля колес, имеющих изолированные неровности, от общего числа однотипных колес, остальные из которых имеют непрерывные неровности (принять равной 0,05).
Слайд 17
где Iр – момент инерции рельса рассматриваемого типа
при износе 0 мм (для рельсов типа Р65
= 0,87);
ε – коэффициент, учитывающий влияние жесткости пути (материал и конструкция шпалы) на образование динамической неровности пути по сравнению с деревянными шпалами;
γ – коэффициент, учитывающий влияние рода балласта на образование динамической неровности пути;
lш – расстояние между осями шпал, м;
U – модуль упругости подрельсового основания, МПа;
qк – неподрессоренная масса, отнесенная к одному колесу, Н;
k – коэффициент относительной жесткости пути рельсового основания и рельса, м-1, определяемый по формуле
E – модуль упругости материала балки (для рельсовой стали E = 2,1·105 МПа);
Iz – момент инерции поперечного сечения балки (рельса), относительно центральной оси, м4.
Слайд 22
1.3 Эквивалентные нагрузки
1.3.1 Общие положения
При движении поезда на
путь воздействует система сосредоточенных сил – давление от колес
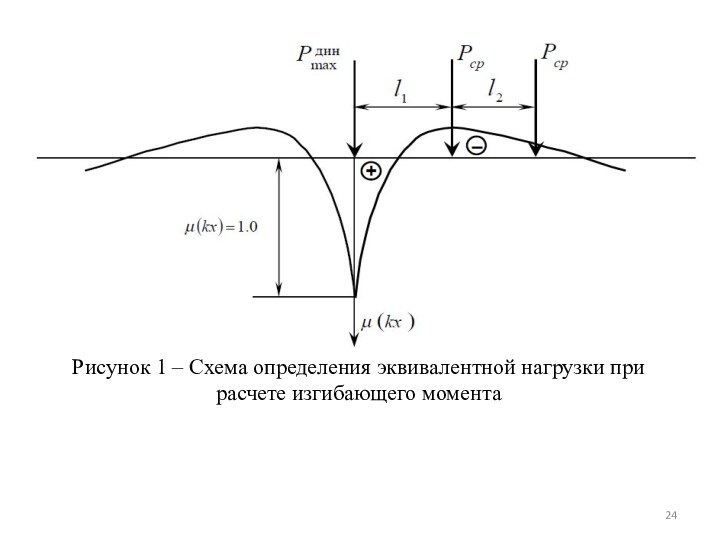
тележек. Самым невыгодным (опасным) положением такой подвижной нагрузки для расчетного сечения является расположение одного из колес на вершине линии влияния. Учитывая то, что линии влияния изгибающих моментов и прогибов принятой модели пути быстро затухают, достаточно рассмотреть систему сил, состоящую из давлений трех последовательно расположенных колес. Нагрузку, определяемую как сумму воздействия усилий от каждого из включенных в расчетную схему колес в данном сечении, называют эквивалентной нагрузкой.
При определении эквивалентных нагрузок считается, что одно из колес тележки локомотива или вагона передает на рельс расчетную нагрузку, а другие – среднюю (т. е. вероятный максимум динамической нагрузки расчетного колеса не совпадает с максимумом нагрузок соседних колес).
Слайд 24
Рисунок 1 – Схема определения эквивалентной нагрузки при
расчете изгибающего момента
Слайд 28
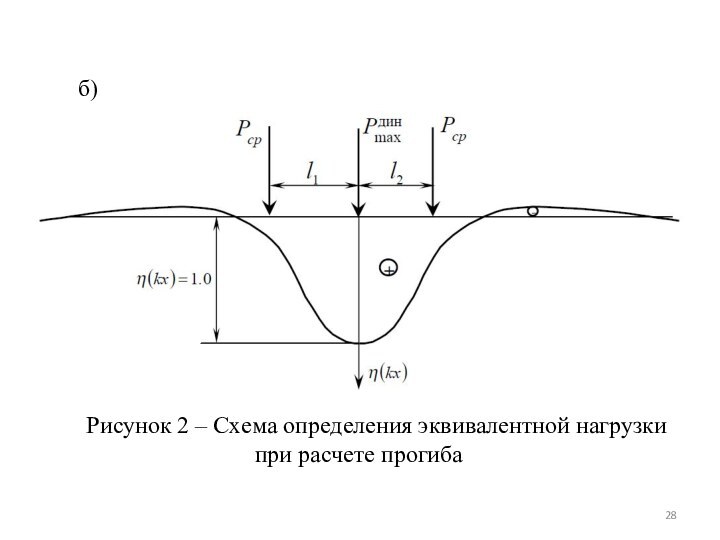
Рисунок 2 – Схема определения эквивалентной нагрузки
при расчете
прогиба
б)
Слайд 30
1.4 Определение изгибающего момента, прогиба и давления рельса
на шпалу
Изгибающий момент в рельсе от воздействия эквивалентной нагрузки
определяется по формуле, Н·м
M = …
Максимальный прогиб рельса, м
y = …
Приближенное давление рельса на шпалу определяется как
Q0 = …
.
.
.
Слайд 31
1.5 Определение напряжений в элементах верхнего строения пути
1.5.1
Осевые напряжения в подошве рельса
Максимальные осевые напряжения в
подошве рельса от изгиба и вертикальной нагрузки определяются по формуле
,
где W – момент сопротивления поперечного сечения рельса относительно нейтральной оси для удаленного волокна подошвы, м3.
σпо = …
Слайд 32
1.5.2 Кромочные напряжения в подошве рельса
Вертикальная нагрузка
от колеса на рельс имеет смещение (эксцентриситет) относительно оси
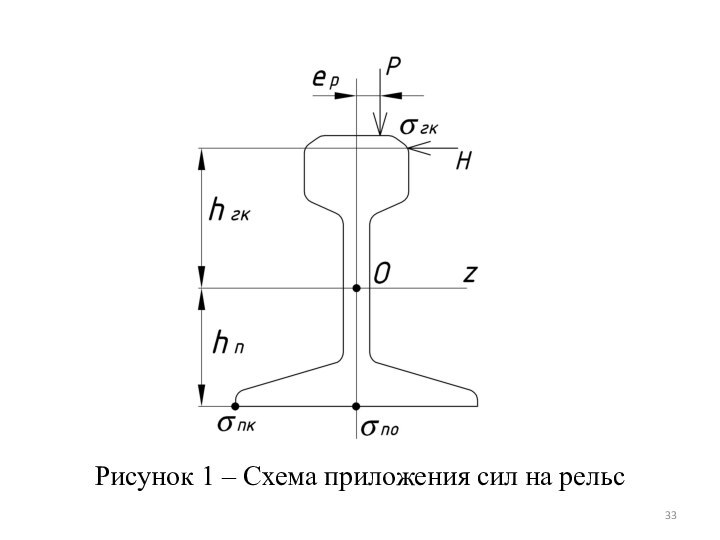
симметрии сечения рельса. Со стороны гребня колеса на головку рельса действует горизонтальная сила (рисунок 1). Вследствие этого в наиболее удаленных точках от центральных осей поперечного сечения рельса (наружная кромка подошвы и внутренняя кромка головки рельса) возникает сложное напряженное состояние от совместного действия двух изгибающих моментов и крутящего момента.
Слайд 33
Рисунок 1 – Схема приложения сил на рельс
Слайд 34
Нормальные напряжения в кромке подошвы рельса вычисляются по
формуле, Па
,
где f – коэффициент перехода
к кромочным напряжениям, зависящий от типа экипажа, радиуса кривой (п.1.1.2 под номером 9)
σпк = …
Слайд 35
1.5.3 Напряжения в шпалах и в балластном слое
под шпалой
Напряжения смятия в деревянных шпалах под подкладками и
в прокладках при железобетонных шпалах определяются по формуле
,
где ω – площадь подкладки или подрельсовой прокладки, м2.
σш = …
Слайд 36
Напряжения в балластном слое под шпалой в подрельсовом
сечении
где Ωα – эффективная опорная площадь полушпалы с учетом
изгиба, м2.
σб = …
Слайд 38
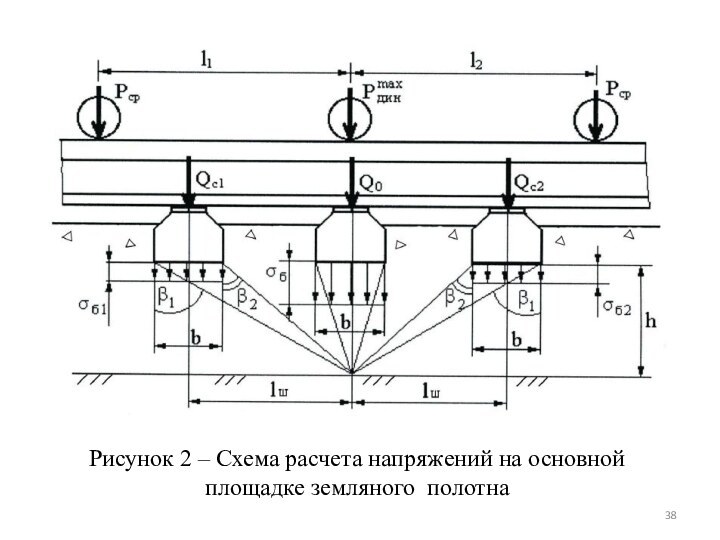
Рисунок 2 – Схема расчета напряжений на основной
площадке земляного полотна
Слайд 39
Напряжения на основной площадке земляного полотна σh на
глубине h определяются под расчетной шпалой с учетом давлений,
передаваемых двумя соседними шпалами, Па
где σh0 – напряжения от действия расчетной шпалы на глубине h от ее подошвы;
σh1, σh2 – напряжения от действия соседних шпал на глубине h от ее подошвы.
Нормальные вертикальные напряжения на глубине h от расчетных давлений под подошвами шпал σб, σб1, σб2 определяются на основе решения плоской задачи теории упругости при рассмотрении шпального основания как однородной изотропной среды по формулам
Слайд 40
где σб, σб1, σб2 – напряжения в балласте
под расчетной и соседними шпалами, определяемые как
(1)
(2)
(3)
(4)
(5)
(6)
Слайд 41
В формулах (4) – (6) Qc1 и Qc2
– давления на соседние шпалы, определяются по формулам
Слайд 42
В формулах (1) – (3) r1 – параметр,
учитывающий влияние материала шпал на напряжения, m1 – коэф-фициент,
учитывающий неравномерность напряже-ний по ширине шпалы и определяемый как
но не менее 1;
С1, С2, Ah – константы, зависящие от геометрии шпального основания (ширины подошвы шпалы b, м, толщины балласта h, м, расстояния между осями шпал lш, м), определяемые по формулам
Слайд 45
1.7 Допускаемые напряжения
Расчет рельсов и других элементов пути
на прочность ведется по допускаемым напряжениям, которые ограничивают максимальные
расчетные напряжения от поездной нагрузки
В соответствии с характером работы каждого из элементов пути регламентируются следующие виды допускаемых напряжений (оценочные критерии прочности пути), обеспечивающих прочность и надежность железнодорожного пути:
Слайд 46
[σк] – допускаемые напряжения растяжения в кромке подошвы
рельса, обусловленные изгибом последнего и кручением от вертикального и
горизонтального воздействия подвижного состава;
[σш] – допускаемые напряжения на смятие в деревянных шпалах под прокладками и в прокладках для железобетонных шпал;
[σб] – допускаемые напряжения сжатия в балласте под шпалой в подрельсовой зоне;
[σh] – допускаемые напряжения сжатия на основной площадке земляного полотна.
Превышение расчетных напряжений над допускаемыми указывает на необходимость усиления пути, причем превышение до 30 % не является основанием для ограничения скорости движения поездов.
Слайд 47
Численные значения допускаемых напряжений в элементах верхнего строения
пути (ВСП) зависят от вида подвижного состава и грузонапряженности
пути (представлены в таблице П. 2.2 /2/).
В рамках курсового проекта будем принимать значения допускаемых напряжений для грузонапряженности более 50 млн т·км брутто/км в год. Однако в кривых радиусом 1000 м и менее рекомендуется принимать значение [σк] = 240 МПа независимо от грузонапряженности. Также при железобетонных шпалах [σш] следует принимать 7,5 МПа для локомотивов и 6,7 МПа для вагонов.
В таблице 1 представлено сравнение допускаемых и расчетных напряжений в элементах ВСП.
Слайд 48
Таблица 1 – Напряжения в элементах верхнего строения
пути
Слайд 49
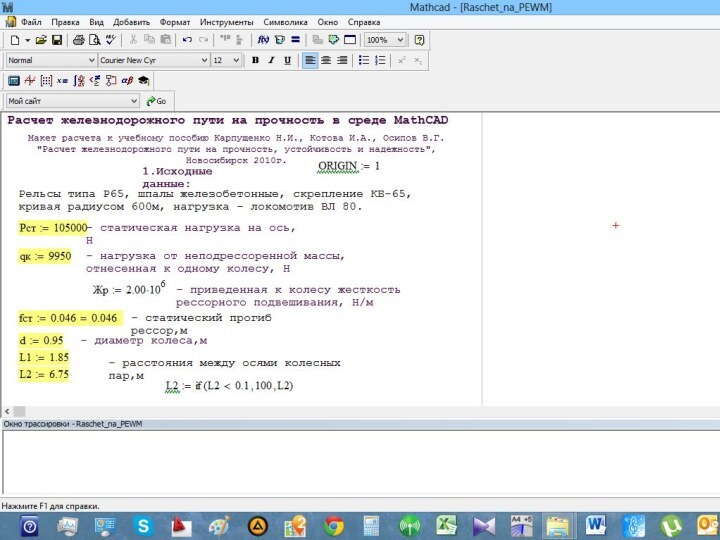
1.8 Расчет пути на прочность на ПЭВМ
Алгоритм расчета
пути на прочность , изложенный в разделах 1.1 –
1.7 реализован в инструментальной среде MathCAD, позволяющей выполнять многоваринтные вычисления для различных конструкций пути и типов подвижного состава.
Для удобства ввода информации в расчетный модуль заполним таблицу 1, содержащую исходные данные по выполнению расчета от воздействия на путь локомотива и вагона (согласно варианту задания).
Слайд 50
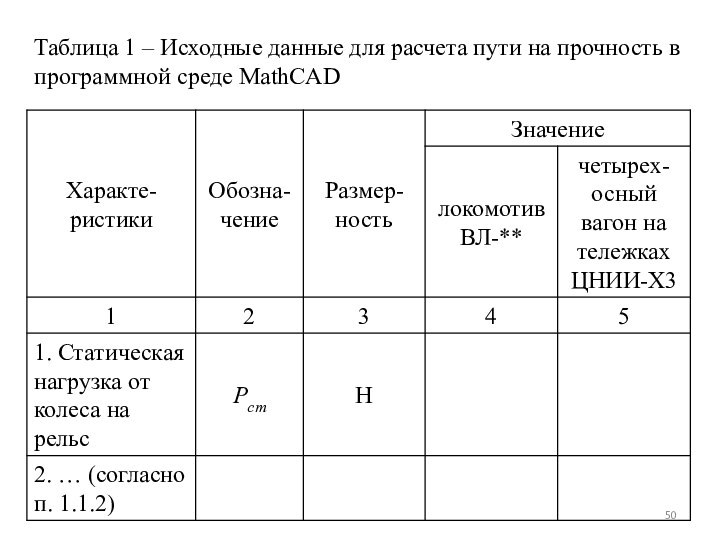
Таблица 1 – Исходные данные для расчета пути
на прочность в программной среде MathCAD
Слайд 51
В таблице 1:
скорость движения экипажа разбить на 4
интервала (v/4, 2*(v/4), 3*(v/4),v);
модуль упругости записать для 4
вариантов условий – лето прямая, лето кривая, зима прямая, зима кривая;
коэффициент, учитывающий горизонтальные силы, и расстояние между осями шпал взять для прямого и кривого участка.
Слайд 60
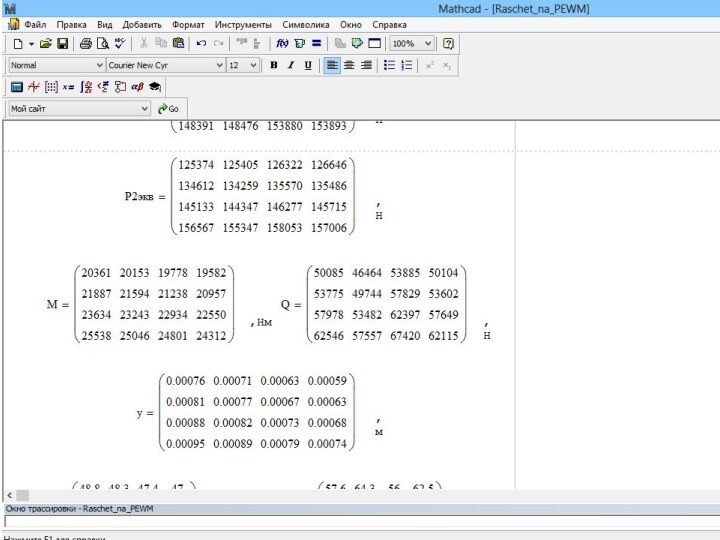
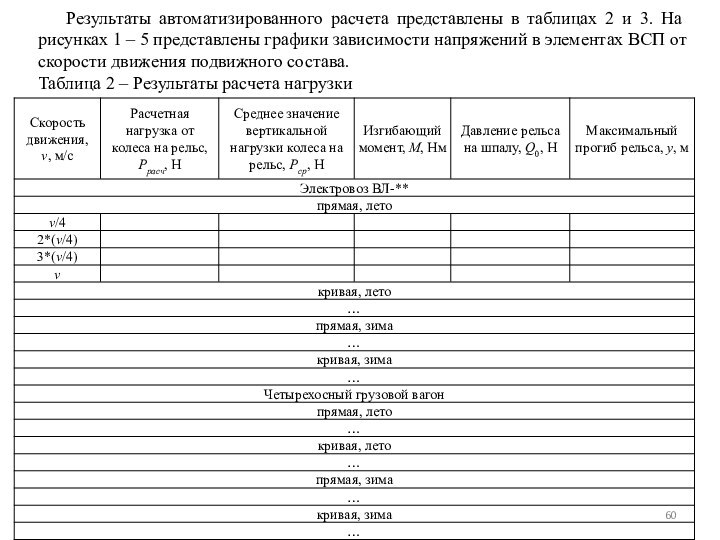
Результаты автоматизированного расчета представлены в таблицах 2 и
3. На рисунках 1 – 5 представлены графики зависимости
напряжений в элементах ВСП от скорости движения подвижного состава.
Таблица 2 – Результаты расчета нагрузки
Слайд 61
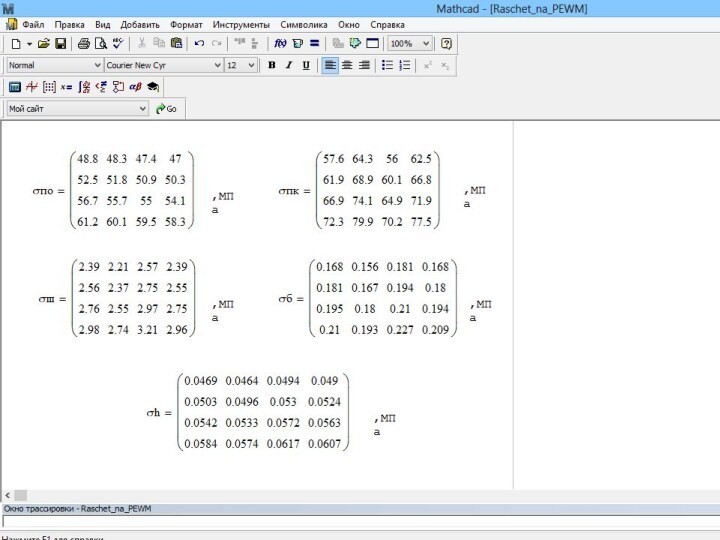
Таблица 3 – Результаты расчета напряжений
Слайд 62
На рисунках 1 – 5 представлены графики зависимости
напряжений в элементах верхнего строения пути от скорости движения
(в соответствии с таблицей 3 составить 5 графиков).
Слайд 63
Рисунок 1 – Зависимость осевых напряжений в подошве
рельса от скорости движения электровоза ВЛ-**
– прямая летом;
– кривая летом;
– прямая зимой;
– кривая зимой
[σк]=240 МПа




















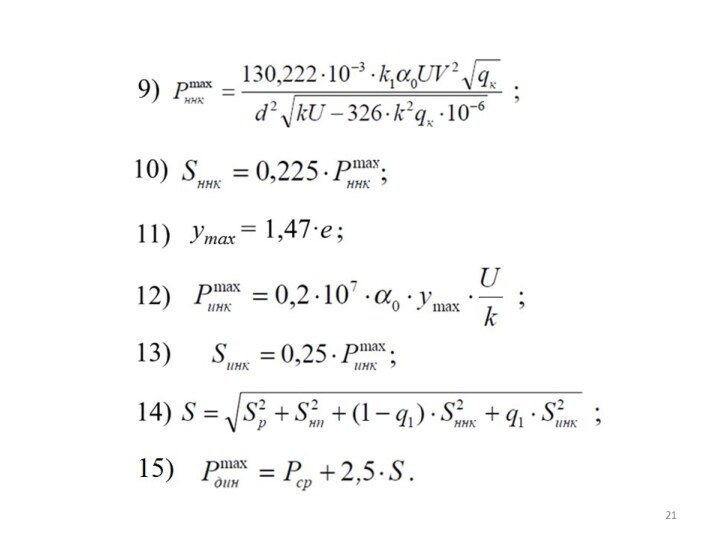

















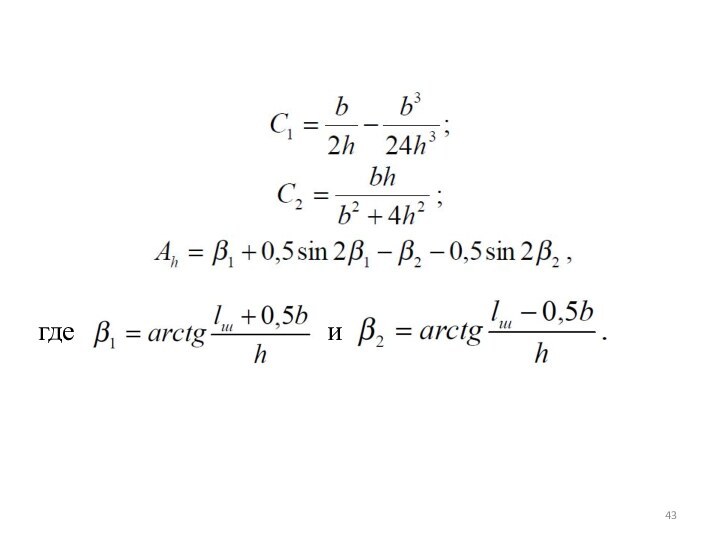


![Цель изучения дисциплины [σк] – допускаемые напряжения растяжения в кромке подошвы рельса, обусловленные изгибом последнего](/img/tmb/14/1343127/619c6c150ba9e676a24e222ecd79928c-720x.jpg)