Слайд 2
U-критерий
Манна – Уитни
Алгоритм U-теста:
1) обе выборки соединяются в
единую выборку. При этом запоминается, к какой выборке относится
каждый элемент массива
2) общая выборка ранжируется по возрастанию
Правила ранжирования:
меньшему значению начисляется меньший ранг
наименьшему значению начисляется ранг 1
наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений n1+n2
Слайд 3
U-критерий
Манна – Уитни
Правила ранжирования:
в случае, если несколько значений
равны, им начисляется ранг, представляющий собой среднее значение тех
рангов, которые они получили бы, если бы они не были равны
общая сумма рангов должна совпадать с расчетной,
которая определяется по формуле
где Ri – ранги,
N=n1+n2 – общее количество ранжируемых наблюдений
Слайд 4
U-критерий
Манна – Уитни
Алгоритм U-теста:
3) разбить единую выборку на
прежние две выборки
4) подсчитать сумму рангов отдельно по каждой
выборке.
Проверить, совпадает ли общая сумма рангов с расчетной
Слайд 5
U-критерий
Манна – Уитни
Алгоритм U-теста:
5) найти эмпирическое значение критерия.
Для этого подсчитать:
где n1 – объем первой выборки,
n2 –
объем второй выборки,
R1 и R2 –ранговые суммы групп
Слайд 6
U-критерий
Манна – Уитни
Алгоритм U-теста:
5) найти критическое значение критерия
Uкрит по таблицам
Слайд 7
U-критерий
Манна – Уитни
Алгоритм U-теста:
6) сравнить эмпирическое и критическое
значение критерия
Если Uэмп>Uкрит, то нулевая гипотеза принимается
Если U эмпUкрит,
то нулевая гипотеза отклоняется
Слайд 8
U-критерий
Манна – Уитни
Ограничения применимости критерия
в каждой из выборок
должно быть не менее 3 значений признака. Допускается, чтобы
в одной выборке было два значения, но во второй тогда не менее пяти.
в каждой выборке должно быть не более 60 наблюдений (ограничение не является строгим для случая компьютерной обработки)
Слайд 9
U-критерий
Манна – Уитни
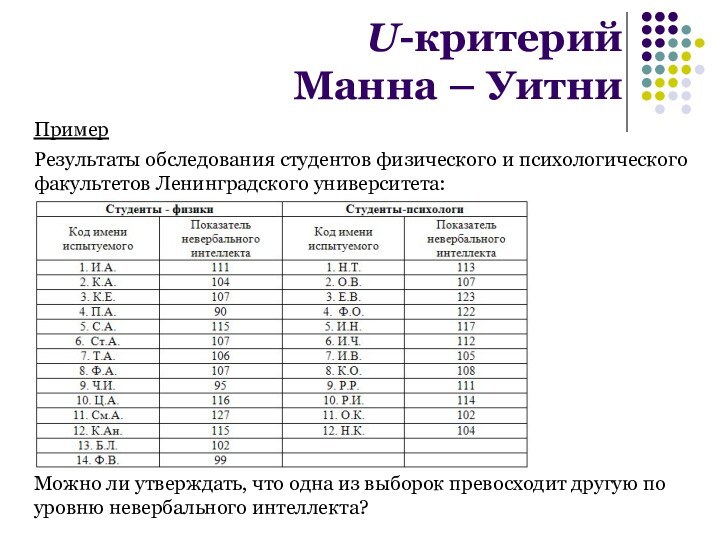
Пример
Результаты обследования студентов физического и психологического
факультетов Ленинградского университета:
Можно ли утверждать, что одна из выборок
превосходит другую по уровню невербального интеллекта?
Слайд 10
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
1) Занести показатели в первый и второй столбец
Найти
объем каждой выборки
Слайд 11
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
2) Выполнить операцию ранжирования
=РАНГ(A3;$A$3:$B$16;1)+(СЧЁТЕСЛИ($A$3:$B$16;A3)-1)/2
Слайд 12
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
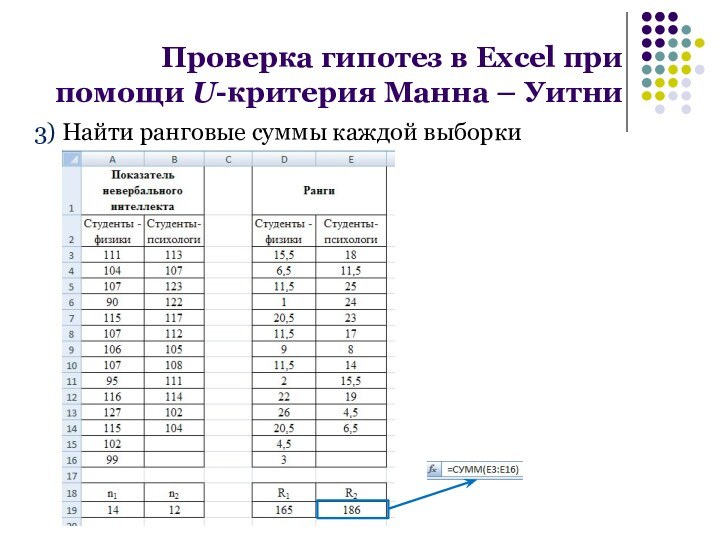
3) Найти ранговые суммы каждой выборки
Слайд 13
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
Так как R1=165
студентов-психологов не превосходит группу студентов-физиков по уровню невербального интеллекта»
Н1: «Группа студентов-психологов превосходит группу студентов-физиков по уровню невербального интеллекта»
Слайд 14
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
5) Подсчитать значение U-критерия по каждой выборке
Слайд 15
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
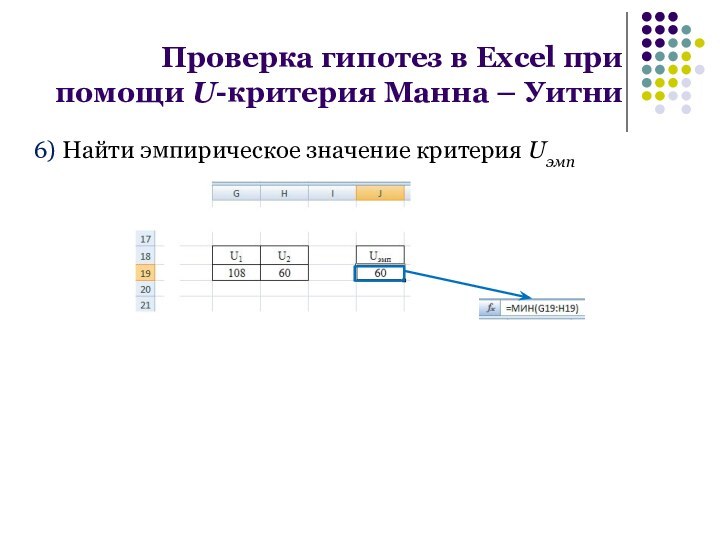
6) Найти эмпирическое значение критерия Uэмп
Слайд 16
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
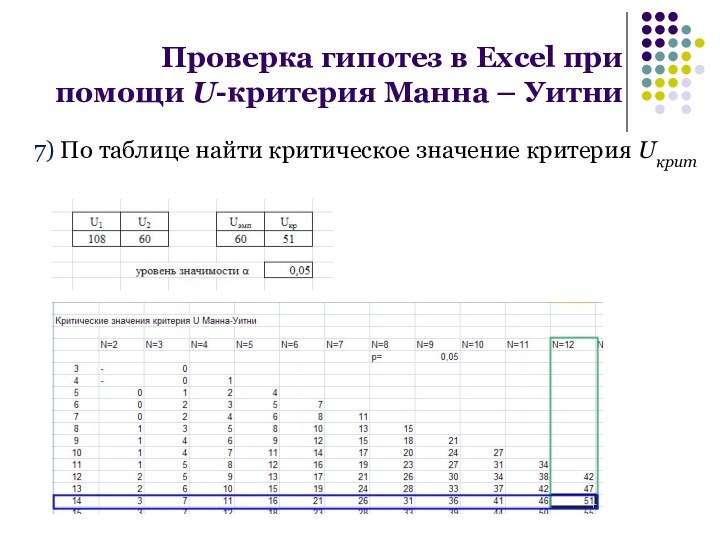
7) По таблице найти критическое значение критерия Uкрит
Слайд 17
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
8) Сравнить эмпирическое Uэмп и критическое Uкрит значение
критерия
Так как то нулевая гипотеза H0 принимается на уровне значимости α=0,05
Вывод: статистически значимое превосходство группы студентов-психологов над группой студентов-физиков по уровню невербального интеллекта не обнаружено
Слайд 18
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
Примечание
Если нет возможности найти критическое значение критерия
Uкрит, то нужно подсчитать по эмпирическому значению критерия уровень Uэмп значимости p
Если уровень значимости p≤α, то нулевая гипотеза H0 принимается
Если уровень значимости p>α, то нулевая гипотеза H0 отклоняется
Слайд 19
Проверка гипотез в Excel при помощи U-критерия Манна
– Уитни
Примечание
=2*(1-НОРМСТРАСП((A19*B19/2-J19)/КОРЕНЬ(A19*B19/12*(A19+B19+1))))
Слайд 20
Проверка гипотез в STATISTICA при помощи U-критерия Манна
– Уитни
1) Занести все показатели в один столбец
Промаркировать показатели:
1
– для первой выборки,
2 – для второй выборки
Слайд 21
Проверка гипотез в STATISTICA при помощи U-критерия Манна
– Уитни
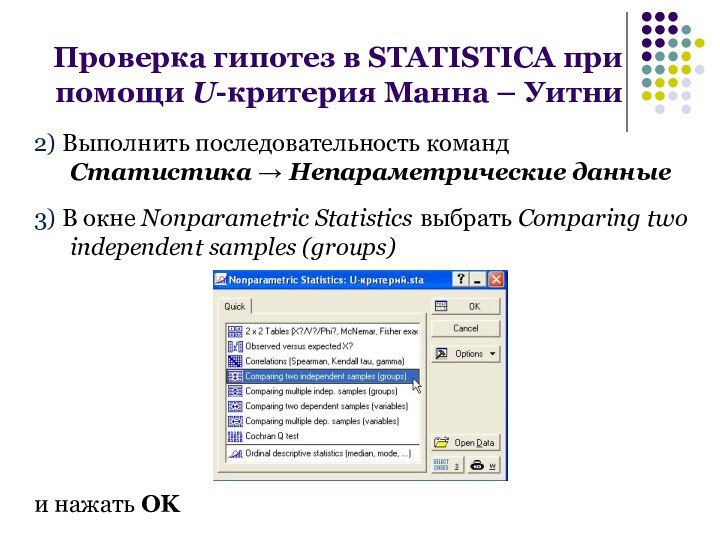
2) Выполнить последовательность команд
Статистика Непараметрические данные
3) В
окне Nonparametric Statistics выбрать Comparing two independent samples (groups)
и нажать OK
Слайд 22
Проверка гипотез в STATISTICA при помощи U-критерия Манна
– Уитни
4) Нажать кнопку Variable и выбрать
в левом
окне (зависимая переменная) – первую переменную,
в правом (группированная переменная) – вторую переменную
и нажать OK
Слайд 23
Проверка гипотез в STATISTICA при помощи U-критерия Манна
– Уитни
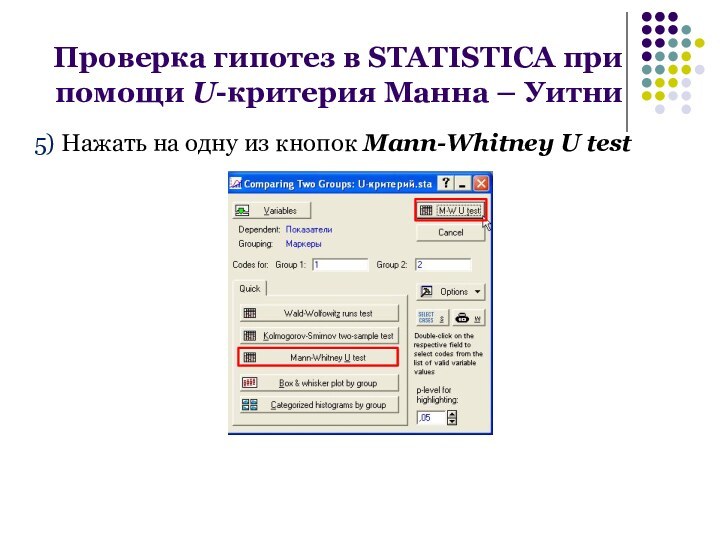
5) Нажать на одну из кнопок Mann-Whitney U
test
Слайд 24
Проверка гипотез в STATISTICA при помощи U-критерия Манна
– Уитни
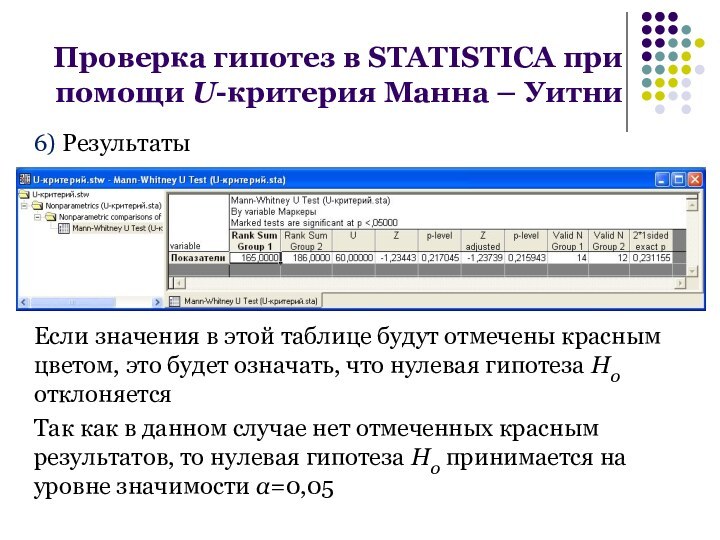
6) Результаты
Если значения в этой таблице будут отмечены
красным цветом, это будет означать, что нулевая гипотеза H0 отклоняется
Так как в данном случае нет отмеченных красным результатов, то нулевая гипотеза H0 принимается на уровне значимости α=0,05