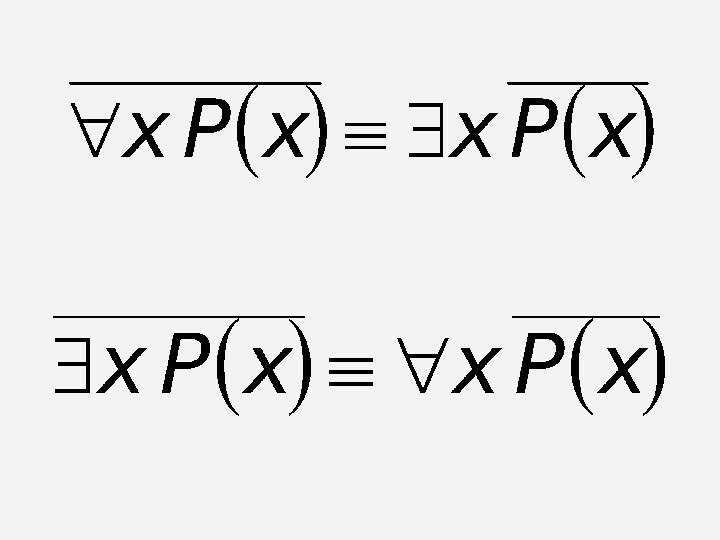Слайд 2
Тема:ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ
ЛОГИКА
Слайд 3
ПРЕДИСЛОВИЕ
толковый словарь С. И. Ожегова :
Логика
- наука о законах мышления и его формах
Слово "логика"
происходит от греческого logos, что, с одной стороны, означает "слово", а с другой - "мысль, рассуждение".
Логика изучает акты мышления, зафиксированные в языке в виде слов, предложений и их совокупностей.
польский логик А. Тарский:
Логика создает возможность лучшего взаимопонимания между теми, кто к этому стремится.
Слайд 4
Логика как наука сформировалась очень давно в IV
в. до н.э. Ее создал древнегреческий ученый Аристотель.
АРИСТОТЕЛЬ
(лат. Aristotle) (384 до н. э., Стагира, полуостров Халкидика, Северная Греция — 322 до н. э., Халкис, остров Эвбея, Средняя Греция), древнегреческий ученый, философ, основатель Ликея, учитель Александра Македонского.
Отец Аристотеля — Никомах, был врачом при дворе македонских царей. Он сумел дать сыну хорошее домашнее образование, знание античной медицины. Влияние отца сказалось на научных интересах Аристотеля, его серьезных занятиях анатомией. В 367, в возрасте семнадцати лет, Аристотель отправился в Афины, где стал учеником Академии Платона.
Слайд 5
АРИСТОТЕЛЬ (384-322 до н. э.)
в 335 основал Ликей, или перипатетическую школу. Воспитатель Александра
Македонского. Сочинения Аристотеля охватывают все отрасли тогдашнего знания. Основоположник формальной логики. создатель силлогистики. «Первая философия» (позднее названа метафизикой) содержит учение об основных принципах бытия: возможности и осуществлении, форме и материи, действующей причине и цели СИЛЛОГИСТИКА (от греч. syllogistikos — выводящий умозаключение), исторически первое, созданное Аристотелем учение о логической дедукции, в котором рассматриваются рассуждения в форме силлогизмов.
Слайд 6
Сохранившиеся произведения Аристотеля по логике:
свод «Органон»
(труды «Категории», «Об истолковании», первая и вторая «Аналитика», «Топика»);
Аристотель
исследовал различные формы суждений и их комбинаций и ввел понятие силлогизма, т.е. рассуждения, в котором из заданных двух суждений выводится третье. Он выделил все правильные формы силлогизмов, которые можно составить из суждений: «Все а суть в», «Некоторые а суть в», «Все а не суть в», «Некоторые а не суть в».
Слайд 7
Все насекомые - шестиногие.
У паука - не шесть
ног (а восемь!).
Следовательно, паук не насекомое.
Все числа, кратные 10»
оканчиваются нулем.
Число N не оканчивается нулем.
Следовательно, число N не кратно 10.
Эти короткие, одношаговые рассуждения (умозаключения) имеют одну и ту же форму: Все А — это В. не В, Следовательно, не А.
Умозаключение такой формы всегда приводит к верному (истинному) выводу (заключению, следствию), если исходные утверждения посылки) истинны.
Слайд 8
СИЛЛОГИЗМ - РАССУЖДЕНИЕ, В
КОТОРОМ ИЗ ЗАДАННЫХ ДВУХ
СУЖДЕНИЙ ВЫВОДИТСЯ ТРЕТЬЕ.
ВСЕ МЛЕКОПИТАЮЩИЕ ИМЕЮТ СКЕЛЕТ. ВСЕ КИТЫ -
МЛЕКОПИТАЮЩИЕ. СЛЕДОВАТЕЛЬНО,
ВСЕ КИТЫ ИМЕЮТ СКЕЛЕТ.
2. ВСЕ КВАДРАТЫ - РОМБЫ.
ВСЕ РОМБЫ - ПАРАЛЛЕЛЕГРАММЫ. СЛЕДОВАТЕЛЬНО,
ВСЕ КВАДРАТЫ - ПАРАЛЛЕЛОГРАММЫ.
Слайд 9
В течение многих веков логика сколько-нибудь существенно не
развивалась. Это, конечно, свидетельствует о гениальности Аристотеля, которому удалось
создать столь полную научную систему, что, казалось, "неубавить, не прибавить". Однако в силу такой неизменности логика приобрела славу мертвой, застывшей науки и вызывала у многих скептическое к себе отношение.
Слайд 10
Декарт Рене (1596-1650, фр. Философ, математик)
РЕКОМЕНДОВАЛ В
ЛОГИКЕ ИСПОЛЬЗОВАТЬ МАТЕМАТИЧЕСКИЕ МЕТОДЫ.
Слайд 11
В XVII в. великий немецкий ученый Лейбниц
(1646-1716) задумал создать новую логику, которая была бы "искусством
исчисления".
В этой логике, по мысли Лейбница» каждому понятию соответствовал бы символ, а рассуждения имели бы вид вычислений. Эта идея Лейбница, не встретив понимания современников, не получила в то время распространения и развития.
Слайд 12
ЛЕЙБНИЦ (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик,
физик, языковед. С 1676 на службе у ганноверских герцогов.
Основатель и президент (с 1700) Бранденбургского научного общества (позднее — Берлинская АН).
По просьбе Петра I разработал проекты развития образования и государственного управления в России. Предвосхитил принципы современной математической логики («Об искусстве комбинаторики», 1666). Один из создателей дифференциального и интегрального исчислений.
Слайд 13
Только в середине XIX в. ирландский математик и
логик Джордж Будь (1815-1864) частично воплотил в жизнь идею
Лейбница. Им была создана алгебра логики, в которой действуют законы, схожие с законами обычной алгебры, но буквами обозначаются не числа, а предложения.
БУЛЬ Джордж (George Boole) (2 ноября 1815, Линкольн, Великобритания — 8 декабря 1864, Баллинтемпль, Ирландия), английский математик и логик, один из основоположников математической логики. Разработал алгебру логики (булеву алгебру) («Исследование законов мышления», 1854), основу функционирования цифровых компьютеров.
Слайд 14
Д. Буль родился в бедной рабочей семье. Первые
уроки математики получил у отца. Хотя мальчик посещал местную
школу, в общем его можно считать самоучкой. В 12 лет знал латынь, затем овладел греческим, французским, немецким и итальянским языками. В 16 лет уже преподавал в деревенской школе, а в 20 открыл собственную школу в Линкольне. В редкие часы досуга зачитывался математическими журналами Механического института, интересовался работами математиков прошлого — Ньютона, Лапласа, Лагранжа, проблемами современной алгебры.
Слайд 15
Алгебра логики Буля явилась зародышем новой науки -
математической логики.
В отличие от нее логику, восходящую к
Аристотелю, называют классической или традиционной формальной логикой.
Слайд 16
Логика изучает внутреннюю структуру процесса мышления, который реализуется
в таких естественно сложившихся формах как понятие, суждение, умозаключение
и доказательство.
Слайд 17
Понятие - это форма мышления, отражающая наиболее существенные
свойства предмета, отличающие его от других предметов.
В структуре
каждого понятия нужно различать две стороны: содержание и объем.
Слайд 18
Содержание понятия составляет совокупность существенных признаков предмета.
Чтобы
раскрыть содержание понятия, следует выделить признаки, необходимые и достаточные
для выделения данного предмета по отношению к другим предметам.
Слайд 19
Объем понятия определяется совокупностью предметов, на которую оно
распространяется, и может быть представлено в форме множества объектов,
состоящего из элементов множества.
Слайд 20
Высказывание (суждение) - это форма мышления, выраженная с
помощью понятий, посредством которой что-либо утверждают или отрицают о
предметах, их свойствах и отношениях между ними.
Слайд 21
О предметах можно судить верно или неверно, т.е.
высказывание может быть истинным или ложным. Истинным будет суждение,
в котором связь понятий правильно отражает свойства и отношения реальных вещей. Ложным суждение будет в том случае, когда связь понятий искажает объективные отношения, не соответствует реальной действительности.
Слайд 22
Обоснование истинности или ложности простых высказываний решается вне
логики.
Например, истинность или ложность высказывания: "Сумма углов треугольника
равна 180 градусов" устанавливается геометрией, причем — в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
Слайд 23
Умозаключение - это форма мышления, посредством которой из
одного или нескольких суждений, называемых посылками, по определенным правилам
логического вывода получается новое знание о предметах реального мира (вывод).
Умозаключения бывают дедуктивные, индуктивные и по аналогии.
Слайд 24
В дедуктивных умозаключениях рассуждения ведутся от общего к
частному.
Например, из двух суждений:
«Все металлы электропроводны» и
«Ртуть является металлом»
путем умозаключения можно сделать вывод, что:
«Ртуть электропроводна».
Слайд 25
В индуктивных умозаключениях рассуждения ведутся от частного к
общему.
Например, установив, что отдельные металлы - железо, медь,
цинк, алюминий и т.д. - обладают свойством электропроводности, можно сделать вывод, что все металлы электропроводны.
Слайд 26
Умозаключение по аналогии представляет собой движение мысли от
общности одних свойств и отношений у сравниваемых предметов или
процессов к общности других свойств и отношений.
Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце обнаружили неизвестный еще на Земле химический элемент гелий, то по аналогии заключили: такой элемент есть и на Земле.
Слайд 27
Доказательство есть мыслительный процесс, направленный на подтверждение или
опровержение какого-либо положения посредством других несомненных, ранее обоснованных доводов.
Доказательство по своей логической форме не отличается от умозаключения. Однако, если в умозаключении заранее исходят из истинности посылок и следят только за правильностью логического вывода, в доказательстве подвергается логической проверке истинность самих посылок.
Слайд 28
ГЛАВА I. ЛОГИКА ВЫСКАЗЫВАНИЙ
§ 1. Операции над высказываниями
Слайд 29
Под предложением будем понимать соединение слов, имеющее самостоятельный
смысл (лингвистическое понятие).
Высказывание – это повествовательное предложение, о котором
(в определенных условиях) можно сказать, истинно оно или ложно.
Логическим значением высказывания является «истина»(1) и «ложь»(0)
Слайд 30
Примеры высказываний
"Москва - столица России."
"Волга впадает
в Черное море."
«2+2=4.»
«Если 2+2=5, то Омск - столица
России.»
Примеры не высказываний
«2+х=5.»
«Ура!»
«Омск - столица России?»
Слайд 31
Простыми (элементарными) высказываниями называются такие высказывания, которые не
расчленяются на другие высказывания.
Союзы «и», «или», «если... то,..»,
«…тогда и только тогда, когда…..» и частицу «не» (словосочетание «неверно, что…») будем называть логическими связками.
Высказывания , образованные из других высказываний с помощью логических связок (или союзов, к ним сводящихся), называют составными.
Слайд 32
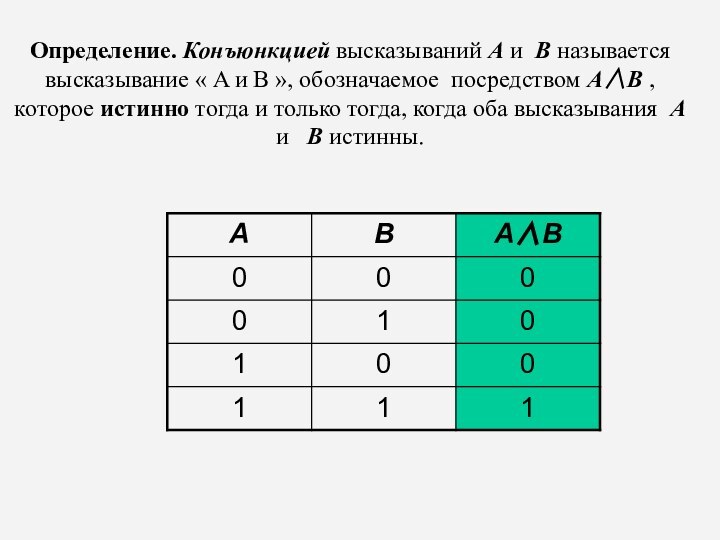
Определение. Конъюнкцией высказываний A и B называется высказывание
« A и B », обозначаемое посредством AB ,
которое истинно тогда и только тогда, когда оба высказывания A и B истинны.
Слайд 33
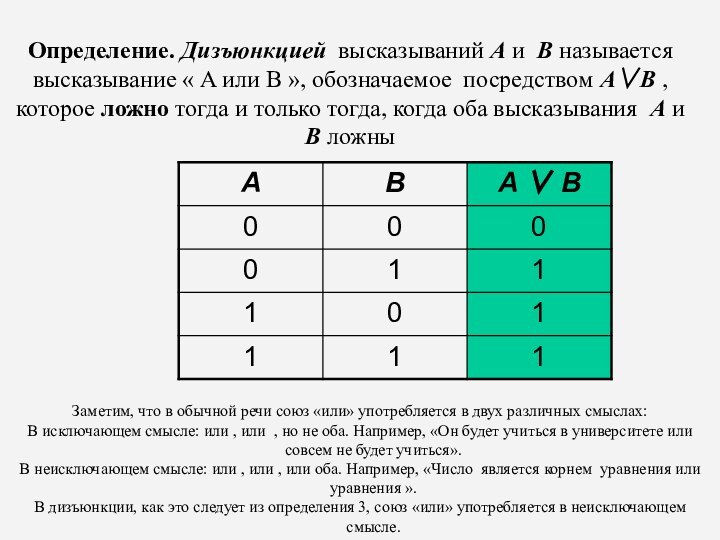
Определение. Дизъюнкцией высказываний A и B называется высказывание
« A или B », обозначаемое посредством AB ,
которое ложно тогда и только тогда, когда оба высказывания A и B ложны
Заметим, что в обычной речи союз «или» употребляется в двух различных смыслах:
В исключающем смысле: или , или , но не оба. Например, «Он будет учиться в университете или совсем не будет учиться».
В неисключающем смысле: или , или , или оба. Например, «Число является корнем уравнения или уравнения ».
В дизъюнкции, как это следует из определения 3, союз «или» употребляется в неисключающем смысле.
Слайд 34
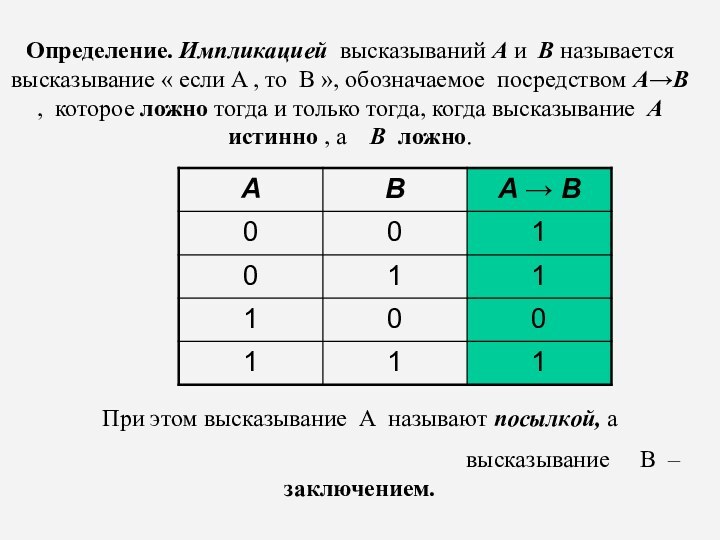
Определение. Импликацией высказываний A и B называется высказывание
« если A , то B », обозначаемое посредством
AB , которое ложно тогда и только тогда, когда высказывание A истинно , а B ложно.
При этом высказывание А называют посылкой, а
высказывание В – заключением.
Слайд 35
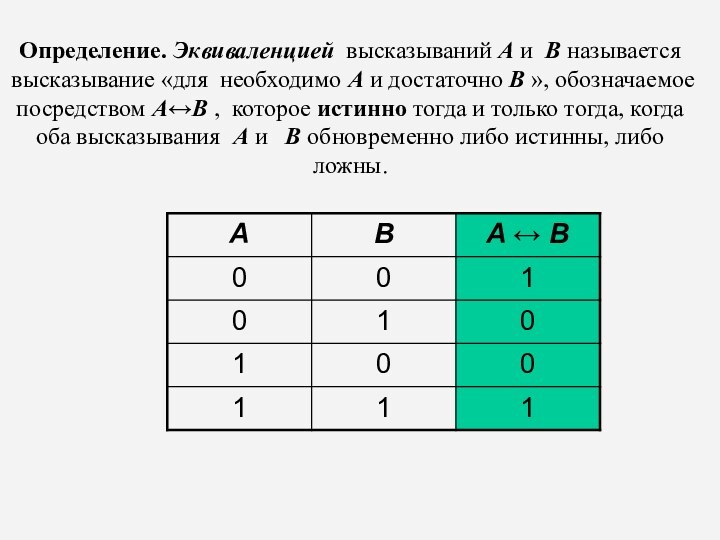
Определение. Эквиваленцией высказываний A и B называется высказывание
«для необходимо А и достаточно В », обозначаемое посредством
AB , которое истинно тогда и только тогда, когда оба высказывания A и B обновременно либо истинны, либо ложны.
Слайд 36
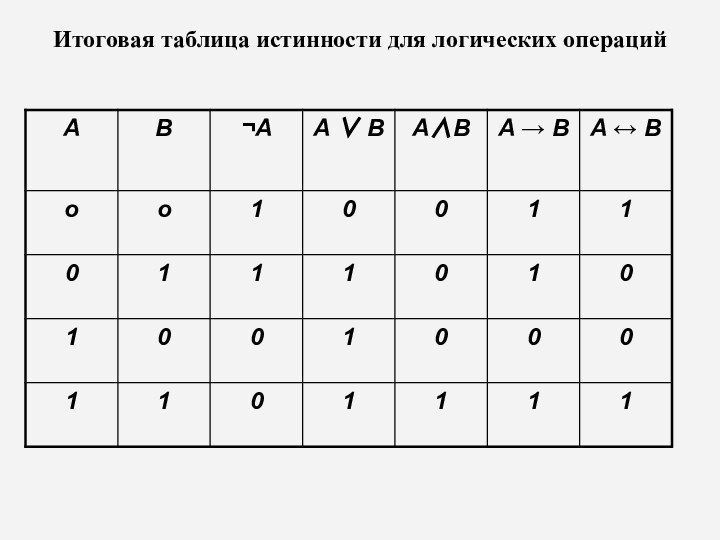
Итоговая таблица истинности для логических операций
Слайд 37
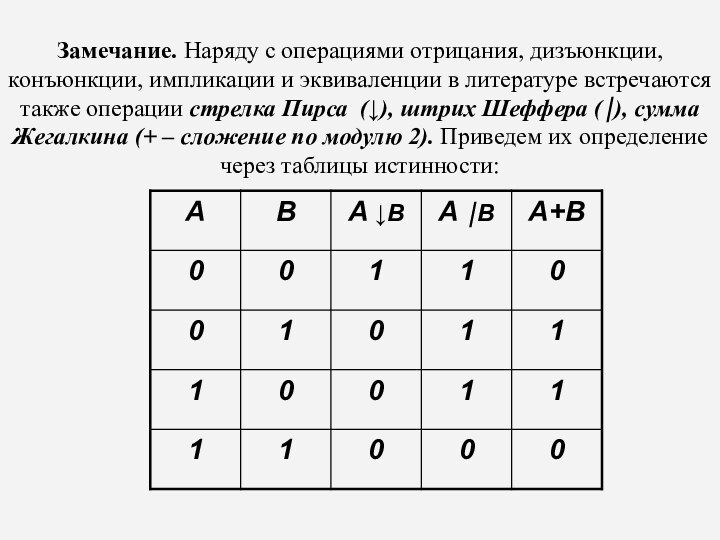
Замечание. Наряду с операциями отрицания, дизъюнкции, конъюнкции, импликации
и эквиваленции в литературе встречаются также операции стрелка Пирса
(), штрих Шеффера (), сумма Жегалкина (+ – сложение по модулю 2). Приведем их определение через таблицы истинности:
Слайд 38
Если известно, в каком именно повествовательном предложении заключается
высказывание, обозначенное символом А, то говорят, что А -
логическая константа.
Пример: А: «Декабрь – зимний месяц».
А – логическая константа.
Его логическое значение никогда не изменяется. Всегда А=1.
Если неизвестно, какое повествовательное предложение обозначено символом А, то говорят, что А - логическая переменная.
Пример: известно только, что А, В, С – высказывания. Значит, А, В, С - логические переменные. Их логические значения точно неизвестны.
Логические константы и логические переменные
Слайд 39
Из логических переменных, символов операций над высказываниями и,
может быть, скобок составляются выражения с логическими переменными.(формулы)
Например,
(АВ)С – выражение с логическими переменными А, В, С.
Выражения с логическими переменными
Слайд 40
Выражения с логическими переменными называются равносильными, если при
каждом наборе логических значений входящих в них простых переменных
эти выражения принимают одно и то же значение.
Обозначение: F1≡ F2 - выражения F1 и F2 равносильны.
Примеры: АВВА АВ ВА
Равносильность выражений с логическими переменными
Слайд 41
Доказать или опровергнуть равносильность выражений с логическими переменными
можно с помощью таблицы истинности.
Пример: докажем равносильность АВ
А В, построив таблицу истинности.
Доказательство равносильности выражений с логическими переменными
сравним
Вывод: при каждом наборе логических значений переменных А и В значения выражений АВ и АВ совпадают. Следовательно, данные выражения равносильны:
АВ ≡ АВ.
Слайд 42
Если при каждом наборе логических значений входящих в
него переменных выражение всегда принимает ложное значение, то данное
выражение называется тождественно-ложным.
Обозначение: F≡0.
Пример: (АВ)(ВА) ≡ 0
Если при каждом наборе логических значений входящих в него переменных выражение всегда принимает истинное значение, то данное выражение называется тождественно-истинным.
Обозначение: F≡1.
Пример: (АВ) (ВА)≡1
Если при некоторых наборах логических значений входящих в него переменных выражение принимает истинное значение, а при других наборах – ложное значение, то такое выражение не является ни тождественно-истинным, ни тождественно-ложным.
Например, АВ – не является ни тождественно-истинным, ни тождественно-ложным.
Тождественно-истинные и тождественно-ложные выражения с логическими переменными
Слайд 45
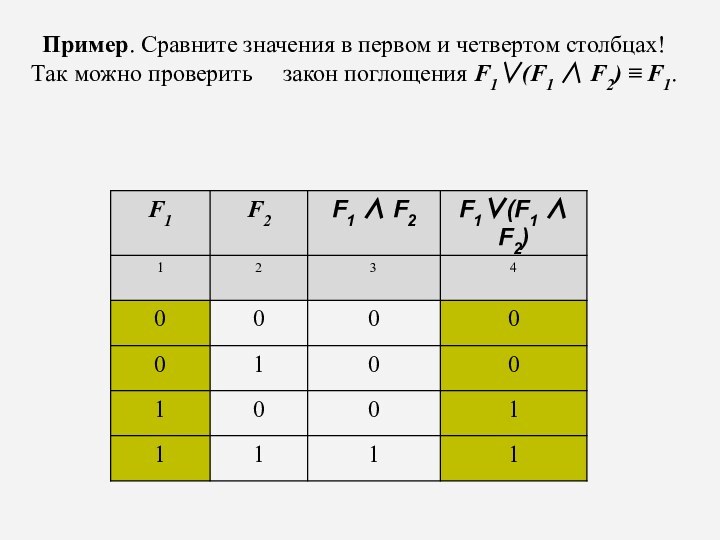
Пример. Сравните значения в первом и четвертом столбцах!
Так можно проверить закон поглощения F1(F1
F2) F1.
Слайд 46
Логическое следование и логическая равносильность
формул алгебры высказываний
Слайд 47
В математике зачастую теоремы имеют вид импликации A
B. Для доказательства их истинности достаточно из истинности высказывания
A логическими рассуждениями вывести истинность высказывания B. В этом случае говорят, что из A логически следует B и пишут A B. При этом высказывание B называют также логическим следствием высказывания A. Аналогичное понятие можно ввести для формул алгебры высказываний.
Слайд 48
Определение. Говорят, что из формулы F логически следует
формула G, и пишут F G , если при
подстановке вместо переменных любых высказываний всякий раз, когда значение формулы F будет истинным высказыванием, значение формулы G также будет истинным высказыванием.
Пример . Доказать, что (X Y) Z X Z
Слайд 49
Т е о р е м а (признак
логического следования для высказывательных формул). Из формулы F логически
следует формула G тогда и только тогда, когда импликация FG является тавтологией.
Слайд 50
Определение. Говорят, что из формул F1, F2,…, Fn
логически следует формула G, и пишут F1, F2,…, Fn
G, если при подстановке вместо переменных любых высказываний всякий раз, когда значение формул
F1, F2,…, Fn будет одновременно истинными высказываниями , значение формулы G также будет истинным высказыванием.
Слайд 51
Теорема . Пусть даны формулы F1, F2,…, Fn
и формула G. Формула G есть логическое следствие F1,
F2,…, Fn тогда и только тогда, когда формула
(( F1F2 … Fn) G) тавтология.
Теорема. Пусть даны формулы F1, F2,…, Fn и формула G. Формула G есть логическое следствие F1, F2,…, Fn тогда и только тогда, когда ((F1 F 2 … Fn G) противоречива.
Слайд 53
Георг Кантор в конце 19 века
создал современную
теорию множеств.
«Множество состоит из элементов.»
Множество может быть
конечным или бесконечным.
«Множество есть многое, мыслимое как единое».
Множества можно сравнивать по «мощности».
Слайд 54
Понятие множества
Под множеством понимают совокупность различных объектов или
явлений, мыслимую как единое целое.
Обозначают множества заглавными буквами
латинского алфавита.
Например, А – множество студентов 1 курса.
Иногда множества имеют особые названия: стадо, труппа, группа, отряд, N, Z, Q, R.
Если х является элементом множества А, пишут: хА.
Если у не является элементом множества А, пишут: уА.
Слайд 55
Способы задания множеств
Перечислением его элементов
А = {a,b,c,d} –
множество А состоит из элементов a,b,c,d.
Например, С = {кукла,
мяч, пирамидка, совок} - множество С состоит из элементов кукла, мяч, пирамидка, совок.
Слайд 56
Способы задания множеств
Не каждое множество можно задать перечислением
элементов.
Бесконечные множества нельзя задать перечислением элементов.
Исключение: бесконечные
множества, для которых ясен порядок образования каждого следующего элемента на основе предыдущего.
Например, множество натуральных чисел – бесконечное. Но известно, что в нём каждое следующее число, начиная со второго, на 1 больше предыдущего.
Поэтому можно задать так: N = {1, 2, 3, 4, …}.
Слайд 57
Способы задания множеств
2. Описанием характеристического свойства
Характеристическое свойство
данного множества – это такое свойство, которым обладают все
элементы этого множества и не обладает ни один элемент, не принадлежащий этому множеству.
Например, D= {ххN Λ х<5}
- множество D состоит из элементов х таких, что хN и х<5.
характеристическое
свойство
Описанием характеристического свойства можно задавать как конечные, так и бесконечные множества.
Слайд 58
Числовые множества
Множества, все элементы которых числа, называются числовыми.
N
= {1, 2, 3, ...} – множество натуральных чисел;
N0
= {0, 1, 2, 3, ...} – множество целых неотрицательных чисел;
Z = {...,-2, -1, 0, 1, 2, ...} – множество целых чисел;
– множество рациональных чисел;
R – множество действительных чисел.
Слайд 59
Способы задания множеств
Одно и то же множество может
быть задано разными способами.
Например, В = {1,2,3}
В = {хxN x<4}
В = {хxN x3}
В= {хxN 0
Существуют множества, которые можно задать только с помощью указания характеристического свойства.
Например, С= {хxR x3}.
Множество С можно записать и как числовой промежуток: C=(-;3].
Слайд 60
Виды числовых промежутков
- [a;b] – закрытый числовой промежуток
от a до b
- [a;b) – полузакрытый слева
числовой промежуток от a до b
- (a;b] – полузакрытый справа числовой промежуток от a до b
- (a;b) – открытый числовой промежуток от a до b
- [a;+) – закрытый числовой полупромежуток от a до +
- (- ;а) – открытый числовой полупромежуток от - до a
- (a;+) – открытый числовой полупромежуток от a до +
- (- ;а] – закрытый числовой полупромежуток от - до a
Слайд 61
Множество, не содержащее элементов, называется пустым и обозначается
Ø.
Например, пустыми являются множество космонавтов в нашей аудитории,
множество груш, созревших на яблоне.
А = {хxN x<0} = Ø, так как нет натуральных чисел, меньших 0.
Пустое множество
Слайд 62
Парадоксы «наивной» теории множеств.
«Парадокс брадобрея»
Брадобрей бреет тех и
только
тех жителей деревни, которые не бреются сами.
Бреет ли
брадобрей себя самого?
Способы преодоления парадоксов.
Ограничиться только
«конструктивно порождаемыми» множествами.
Ограничиться только подмножествами хорошо известных
«универсальных» множеств.
Слайд 63
Отношения между множествами
Включение
Если каждый элемент множества А
является элементом множества В, то говорят, что множество А
включается во множество В,
или множество А – подмножество В.
Обозначение: А В
Например, M={a,b,c,d,x}, К={a,b,c}
К М
Слайд 64
Часто в той или иной математической теории имеют
дело с подмножествами одного и того же множества, которое
называют универсальным в этой теории. Например, в школьной алгебре и математическом анализе универсальным является множество R действительных чисел, в геометрии – множество точек пространства.
Договоримся, что мы всегда находимся в некотором универсальном множестве и будем его обозначать через U,
что пустое множество является подмножеством любого множества.
Слайд 65
2. Равенство
Множества называются равными, если они состоят
из одних и тех же элементов.
Обозначение: А=В.
Например, А={f,k,e},В={k,e,f}
А=В
Отношения между множествами
Слайд 66
Утверждение. Если АВ и В А, то
А=В
Таким образом. чтобы доказать, что множества А и В
равны, достаточно показать, что А является подмножеством множества В и В является подмножеством множества А. Это наиболее общий способ доказательства равенства двух множеств, который называют универсальным.
Слайд 67
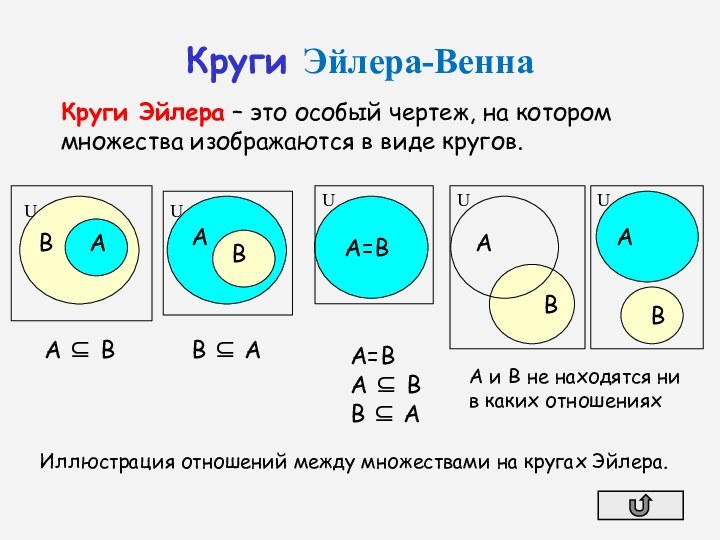
Круги Эйлера-Венна
А
В
А=В
А
В
А
В
А В
А=В А В
В А
Круги Эйлера – это особый чертеж, на
котором множества изображаются в виде кругов.
Иллюстрация отношений между множествами на кругах Эйлера.
А и В не находятся ни в каких отношениях
А
В
В А
U
U
U
U
U
Слайд 70
Операции над множествами
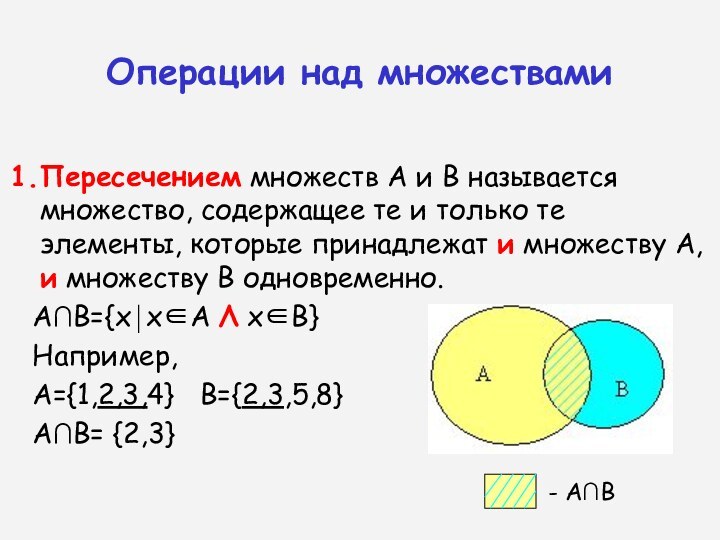
Пересечением множеств А и В называется
множество, содержащее те и только те элементы, которые принадлежат
и множеству А, и множеству В одновременно.
А∩В={ххА Λ хВ}
Например,
А={1,2,3,4} В={2,3,5,8}
А∩В= {2,3}
- А∩В
Слайд 71
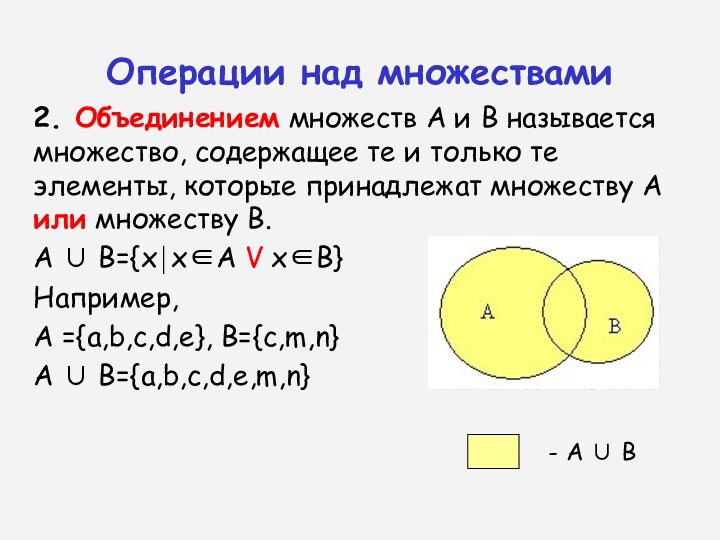
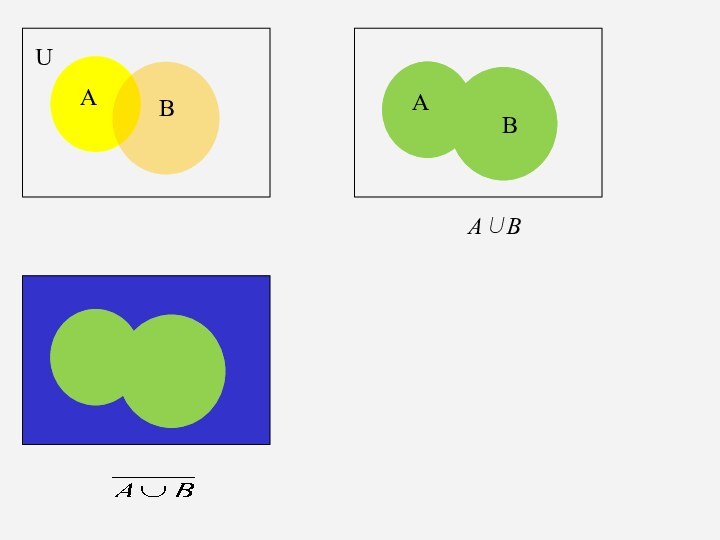
2. Объединением множеств А и В называется множество,
содержащее те и только те элементы, которые принадлежат множеству
А или множеству В.
А В={ххА V хВ}
Например,
А ={a,b,c,d,e}, B={c,m,n}
А В={a,b,c,d,e,m,n}
Операции над множествами
- А В
Слайд 72
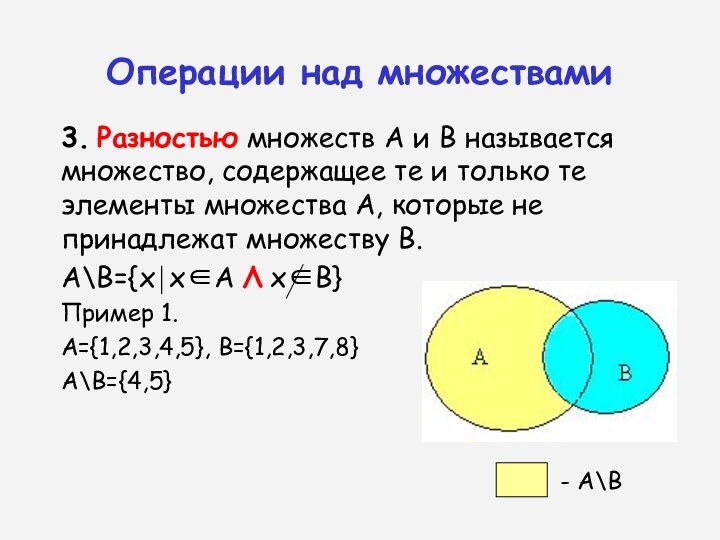
3. Разностью множеств А и В называется множество,
содержащее те и только те элементы множества А, которые
не принадлежат множеству В.
А\В={ххА Λ хВ}
Пример 1.
А={1,2,3,4,5}, В={1,2,3,7,8}
А\В={4,5}
- А\В
Операции над множествами
Слайд 73
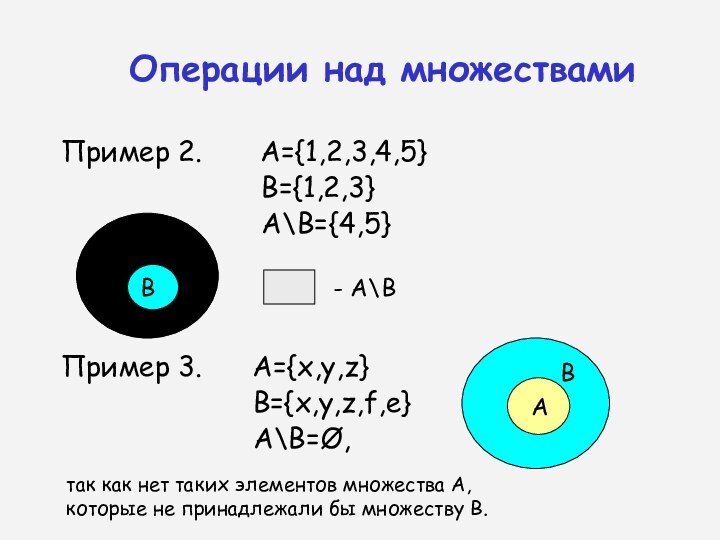
Пример 2. А={1,2,3,4,5}
B={1,2,3}
A\B={4,5}
Пример 3. A={x,y,z}
B={x,y,z,f,e}
A\B=Ø,
B
A
B
А
Операции над множествами
- А\В
так как нет таких элементов множества А, которые не принадлежали бы множеству В.
Слайд 74
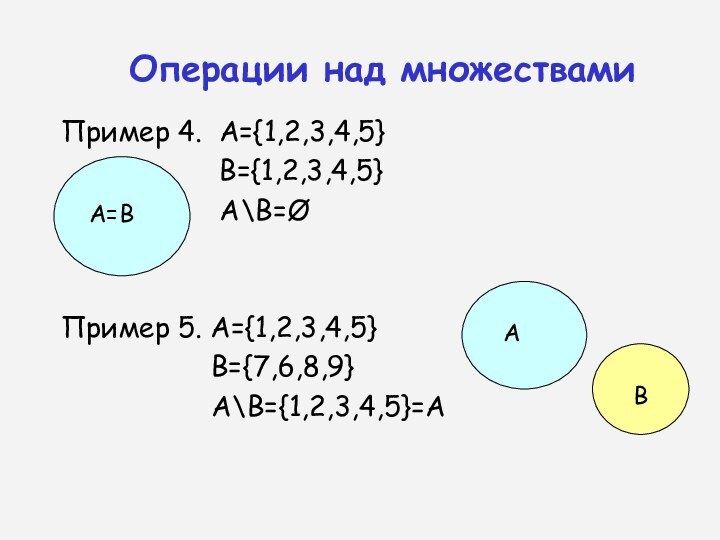
Пример 4. А={1,2,3,4,5}
В={1,2,3,4,5}
A\B=Ø
Пример 5. A={1,2,3,4,5}
B={7,6,8,9}
A\B={1,2,3,4,5}=A
A=B
A
B
Операции над множествами
Слайд 75
Операции над множествами
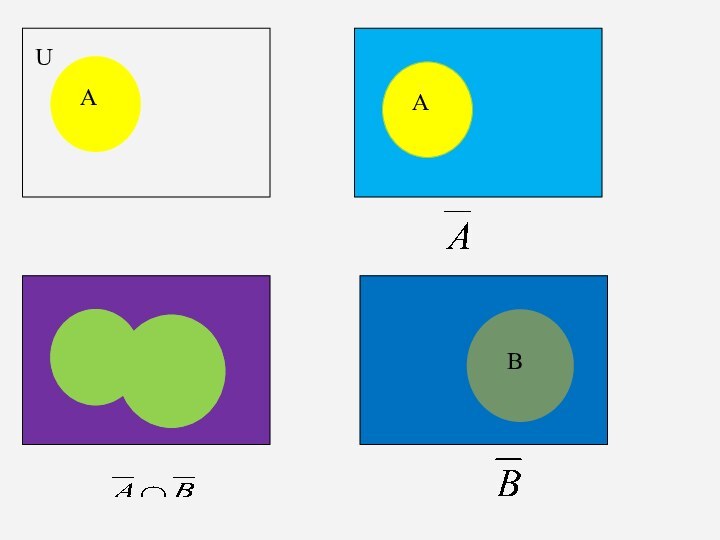
4. Дополнением множества А до универсального
множества U называется множество, содержащее те и только те
элементы множества U, которые не принадлежат множеству A.
А’u={ххU Λ хA}
А’u =
- А’u
Слайд 76
Задача 1
А-множество всех студентов, присутствовавших на лекции;
В – множество студентов группы №1.
Изобразите с
помощью кругов Эйлера.
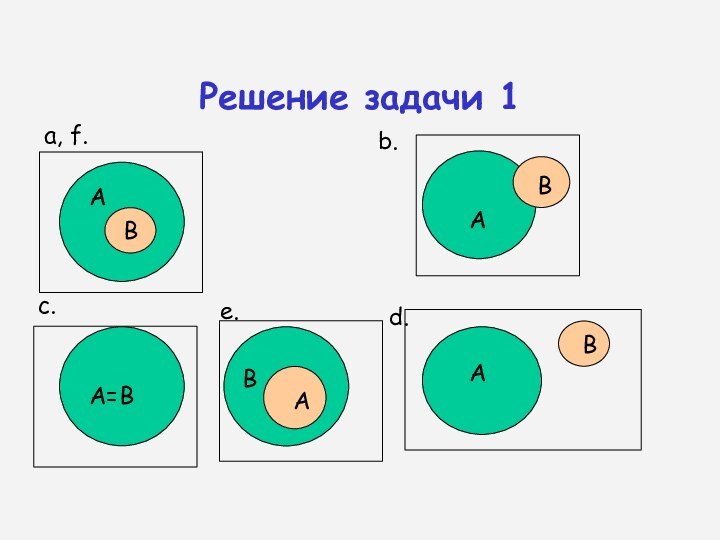
На лекции присутствовали все студенты группы №1 .
На лекции присутствовали некоторые студенты группы №1.
На лекции присутствовали все студенты группы №1 и только они.
На лекции не присутствовал ни один студент группы №1.
Все присутствующие на лекции учатся в группе №1.
Каждый студент группы №1 присутствовал на лекции.
Слайд 77
Решение задачи 1
А
В
А=В
А
В
А
В
a, f.
c.
b.
d.
В
А
e.
Слайд 78
А – множество букв в слове «универмаг»
В –
множество букв в слове «лекторий»
Найти А∩В, АUВ, А\В, В\А.
Задача
2
Решение:
А= {у, н, и, в, е, р, м, а, г},
В = {л, е, к, т, о, р, и, й}
А∩В = {и, е, р}
АUВ = {у, н, и, в, е, р, м, а, г, л, к, т, о, й}
А\В = {у, н, в, м, а, г}
В\А = {л, к, т, о, й}
Слайд 79
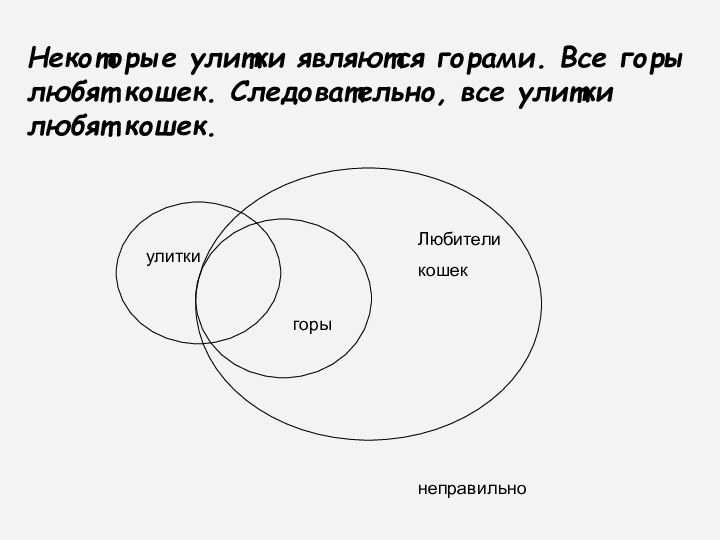
Некоторые улитки являются горами. Все горы любят кошек.
Следовательно, все улитки любят кошек.
улитки
горы
Любители
кошек
неправильно
Слайд 80
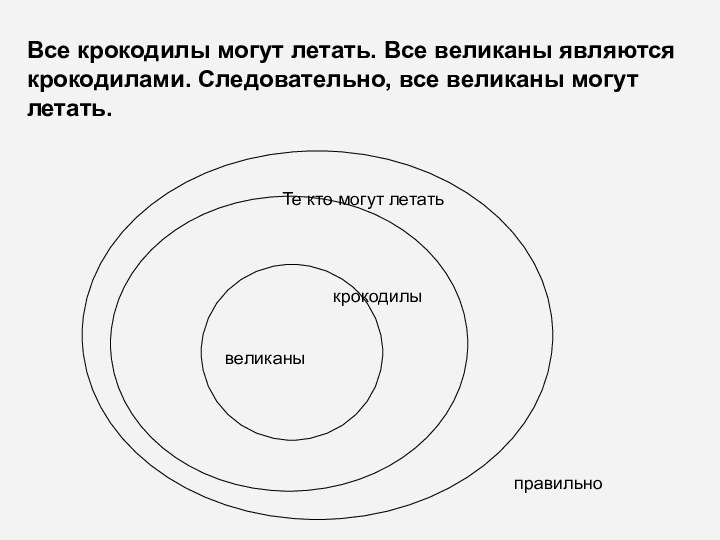
Все крокодилы могут летать. Все великаны являются крокодилами.
Следовательно, все великаны могут летать.
крокодилы
великаны
Те кто могут летать
правильно
Слайд 81
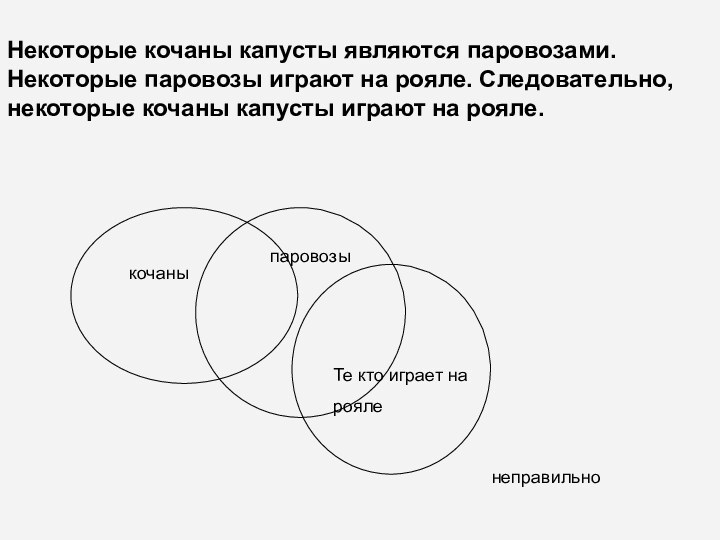
Некоторые кочаны капусты являются паровозами. Некоторые паровозы играют
на рояле. Следовательно, некоторые кочаны капусты играют на рояле.
кочаны
паровозы
Те
кто играет на
рояле
неправильно
Слайд 82
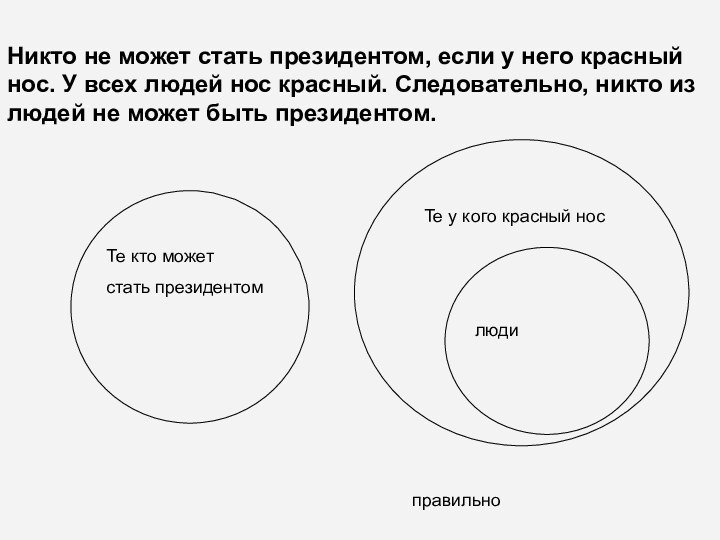
Никто не может стать президентом, если у него
красный нос. У всех людей нос красный. Следовательно, никто
из людей не может быть президентом.
Те кто может
стать президентом
Те у кого красный нос
люди
правильно
Слайд 84
Огастес (Август) де Мо́рган (англ. Augustus de Morgan, 27 июня 1806, Мадура, Индия — 8 марта 1871, Лондон) —
шотландский математик и логик; профессор математики университетского колледжа в Лондоне (1828—1831, 1836—1866); первый президент (1866) Лондонского
математического общества.
Слайд 86
Перечисленные выше равенства справедливы для любых подмножеств A,
B, C универсального множества U (поэтому их и называют
законами алгебры множеств). Доказательство этих формул легко получить универсальным способом доказательства равенства двух множеств.
Слайд 91
Пользуясь формулами 1 – 12, можно производить преобразования
над множественными выражениями, как над числовыми.
Слайд 92
Заметим, что если в равенствах 1–10 заменить на
, на , U на Ø, Ø на U,
то получим соответствующие равенства .
утверждения: если в любом равенстве двух выражений алгебры множеств, не содержащих знака разности, заменить на , на , U на , на U, то вновь получится верное равенство (принцип двойственности теории множеств).
Слайд 94
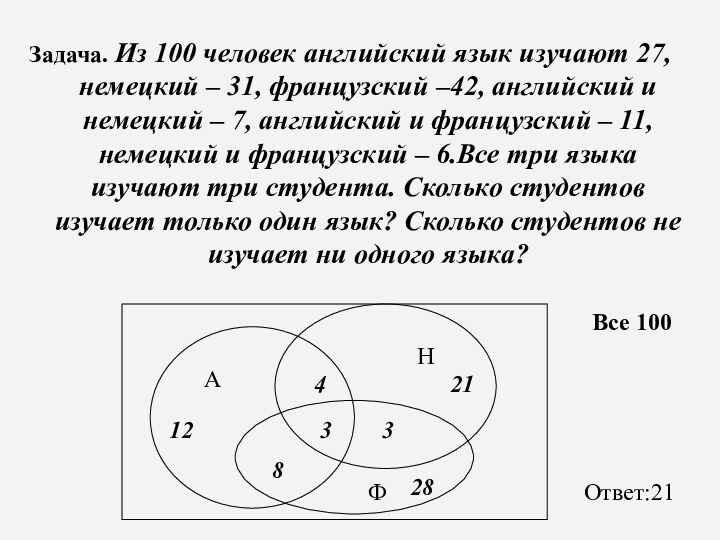
Задача. Из 100 человек английский язык изучают 27,
немецкий – 31, французский –42, английский и немецкий –
7, английский и французский – 11, немецкий и французский – 6.Все три языка изучают три студента. Сколько студентов изучает только один язык? Сколько студентов не изучает ни одного языка?
Все 100
А
Н
Ф
3
4
8
3
12
21
28
Ответ:21
Слайд 95
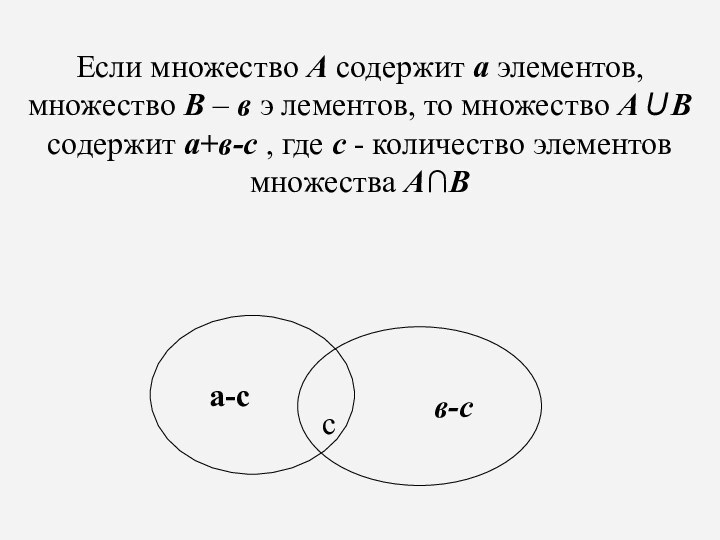
Если множество А содержит а элементов, множество В
– в э лементов, то множество АВ содержит а+в-c
, где с - количество элементов множества AB
с
а-с
в-с
Слайд 96
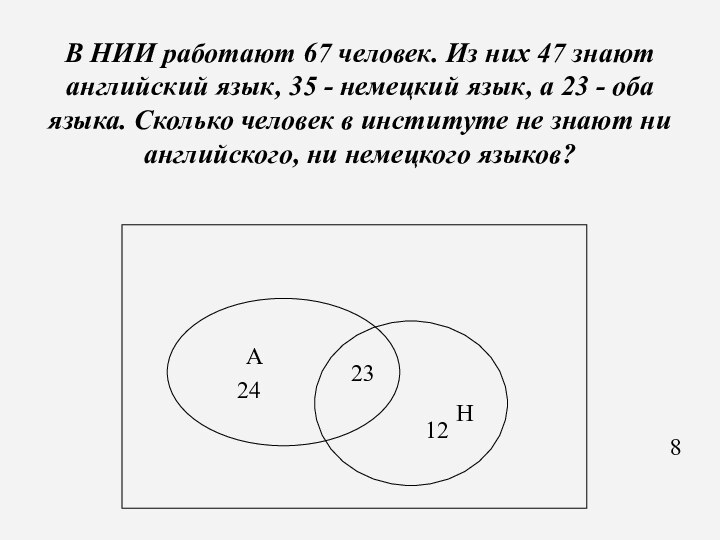
В НИИ работают 67 человек. Из них 47
знают английский язык, 35 - немецкий язык, а 23
- оба языка. Сколько человек в институте не знают ни английского, ни немецкого языков?
А
Н
23
24
12
8
Слайд 97
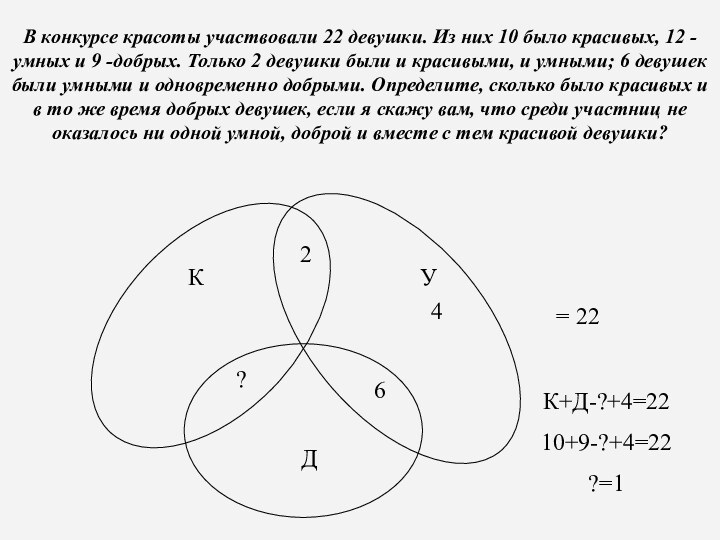
.задача. В конкурсе красоты участвовали 22 девушки. Из
них 10 было красивых, 12 -умных и 9 -добрых.
Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
Слайд 98
В конкурсе красоты участвовали 22 девушки. Из них
10 было красивых, 12 -умных и 9 -добрых. Только
2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
К
У
Д
2
6
4
?
= 22
К+Д-?+4=22
10+9-?+4=22
?=1
Слайд 100
Под упорядоченной парой понимают совокупность двух элементов, каждый
из которых занимает в записи определенное место.
Обозначение: (а; b)
- упорядоченная пара.
Декартовым произведением множеств А и В называется множество всевозможных упорядоченных пар вида (x; y) таких, что xА и yВ.
Обозначение: АВ - декартово произведение множеств А и В.
Символически: АВ = {(x; y)xA yВ}.
Например: А = {, } и В ={,,}.
АВ = {(;), (; ), (; ),(; ), (; ), (; )}
Слайд 101
Соответствием f из множества А во множество В
называется любое подмножество АВ.
Символически: fА В или f:А
В - соответствие f из
множества А во множество В.
область отправления область прибытия.
Например, зададим различные соответствия из множества А = {, } во множество В ={,,}.
f = {(;), (; ), (; ), (; )},
g = {(; ),(; ), (; )},
h = {(; ),(; ), (; )} и т. п.
Слайд 102
Если пара вида (a;b) принадлежит соответствию f, то
b - образ элемента а,
а - прообраз элемента
b при соответствии f.
Например, рассмотрим соответствие
f = {(;), (; )}
из множества А = {, } во множество В ={,,}.
Тогда
- образ - образ
- прообраз - прообраз
при данном соответствии f.
Слайд 103
Способы задания соответствий
1. Перечисление упорядоченных пар
2. Указание характеристического
свойства
3. Граф
4. График
5. Таблица
Слайд 104
Перечисление упорядоченных пар
Упорядоченные пары, принадлежащие данному соответствию, перечисляются
через запятую в фигурных скобках.
Например, пусть А = {1;
2; 3; 4}, B={2;3}.
Зададим f :А В перечислением упорядоченных пар:
f = {(2;2), (3;3);(4;2)}.
Данный способ используется для задания соответствия только между конечными множествами.
Слайд 105
Указание характеристического свойства
Указывается, по какому правилу строятся упорядоченные
пары, принадлежащие соответствию f.
Например, пусть А =
{1; 2; 3; 4}, B={2;3}.
Зададим f :А В указанием характеристического свойства:
f={(x;y)xA yB х у}.
Данный способ используется для задания соответствия как между конечными, так и между бесконечными множествами, но только в том случае, если известно правило, по которому строятся упорядоченные пары, принадлежащие соответствию f.
Слайд 106
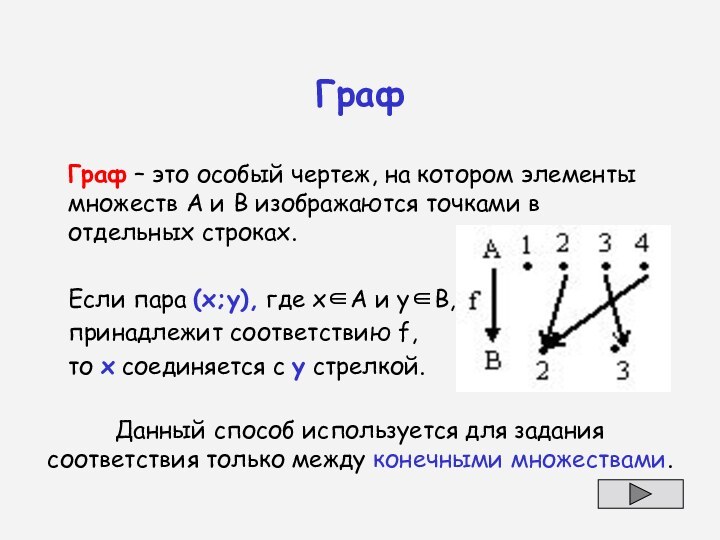
Граф
Граф – это особый чертеж, на котором элементы
множеств А и В изображаются точками в отдельных строках.
Если
пара (х;у), где хА и уВ,
принадлежит соответствию f,
то х соединяется с у стрелкой.
Данный способ используется для задания соответствия только между конечными множествами.
Слайд 107
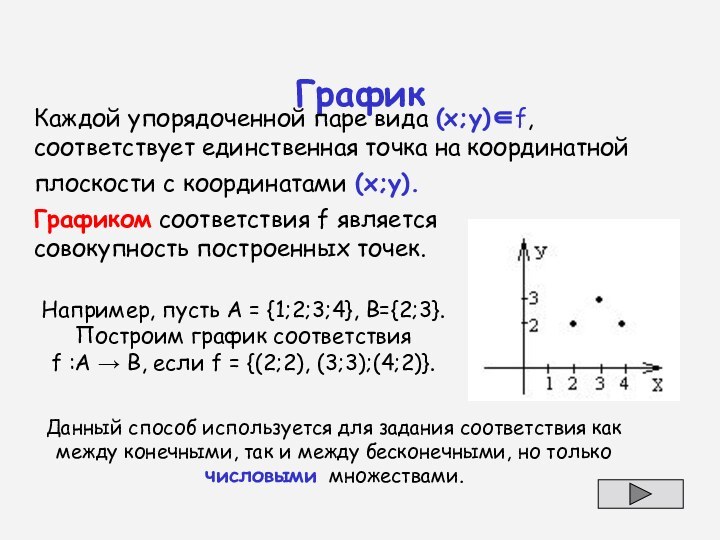
График
Каждой упорядоченной паре вида (х;у)f, соответствует единственная точка
на координатной плоскости с координатами (х;у).
Графиком соответствия f
является совокупность построенных точек.
Данный способ используется для задания соответствия как между конечными, так и между бесконечными, но только числовыми множествами.
Например, пусть А = {1;2;3;4}, B={2;3}.
Построим график соответствия
f :А В, если f = {(2;2), (3;3);(4;2)}.
Слайд 108
Таблица
В первом столбце таблицы записывают элементы множества А,
а в первой строке – элементы множества В.
Если
пара (х;у) принадлежит f:АВ, то в соответствующей клетке таблицы записывается 1.
Если пара (с;d) не принадлежит f:АВ, то в соответствующей клетке таблицы записывается 0.
Например, пусть А = {1;2;3;4}, B={2;3}.
Построим таблицу соответствия
f :А В, если f = {(2;2), (3;3);(4;2)}.
Данный способ используется для задания соответствия только между конечными множествами.
Слайд 109
Областью определения М соответствия f: A B называется
множество элементов, каждый из которых принадлежит множеству А и
имеет хотя бы один образ во множестве В.
Множеством значений Д соответствия f: A B называется множество элементов, каждый из которых принадлежит множеству В и имеет хотя бы один прообраз во множестве А.
Например, соответствие f: АВ,
где А = {-1; 0; 2; 3}, В = {0; 1; 2; 3},
задано c помощью графика.
Областью определения соответствия f является множество М ={-1; 2; 3}, множеством значений - Д = {2; 3}.
Слайд 110
Функции
Соответствие f: AB называется функцией, если каждый элемент
множества А имеет не более одного образа во множестве
В.
Пример 1: Соответствие f: АВ, где А = {х; у; с}, В = {k; h}, задано c помощью графа.
f:АВ – функция, так как каждый
элемент множества А имеет
не более 1 образа во множестве В.
Пример 2: Соответствие f: АВ, где А = {х; у}, В = {w; k; h}, задано c помощью графа.
f: АВ – не является функцией,
так как неверно, что каждый элемент
множества А имеет не более 1 образа
во множестве В.
Существует элемент уА, который имеет
2 образа во множестве В.
Слайд 111
Отображения
Соответствие f: AB называется отображением, если каждый элемент
множества А имеет единственный образ во множестве В.
Пример 1:
Пусть соответствие f: АВ, где А = {х; у; с}, В = {k; h}, задано c помощью графа.
f: АВ – отображение, так как каждый элемент множества А имеет единственный образ во множестве В.
Пример 2: Пусть соответствие f: АВ, где А = {-2; -1; 0; 1;2}, В = {1; 2}, задано c помощью графика.
f: АВ – не является отображением, так как неверно, что каждый элемент множества А имеет единственный образ во множестве В. Существует элемент -2А, который не имеет образов во множестве В.
Слайд 112
Свойства функций и отображений
1. Инъективность
2. Сюръективность
3. Биективность
Слайд 113
Отображение (функция) из множества А во множество В
называется инъективным (инъективной), если каждый элемент множества В имеет
не более одного прообраза во множестве А.
Пример 1: Функция и отображение f: АВ, где А = {у; с}, В = {k; h, х}, является инъективной (ым), так как верно, что каждый элемент множества В имеет не более 1 прообраза во множестве А.
Пример 2: Функция и отображение f: АВ, где А = {х; у; с}, В = {k; h}, не является инъективной (ым), так как неверно, что каждый элемент множества В имеет не более 1 прообраза во множестве А.
Во множестве В существует элемент h, который имеет 2 прообраза во множестве А.
Слайд 114
Отображение (функция) из множества А во множество В
называется сюрьективным (сюрьективной), если каждый элемент множества В имеет
не менее одного прообраза во множестве А.
Пример 1: Функция и отображение f: АВ, где А = {х; у; с}, В = {k; h}, является сюръективной (ым), так как верно, что каждый элемент множества В имеет не менее 1 прообраза во множестве А.
Пример 2: Функция f: АВ, где А = {х; у; с}, В = {k; h}, не является сюръективной, так как неверно, что каждый элемент множества В имеет не менее 1 прообраза во множестве А.
Во множестве В существует элемент k, который не имеет прообразов в А.
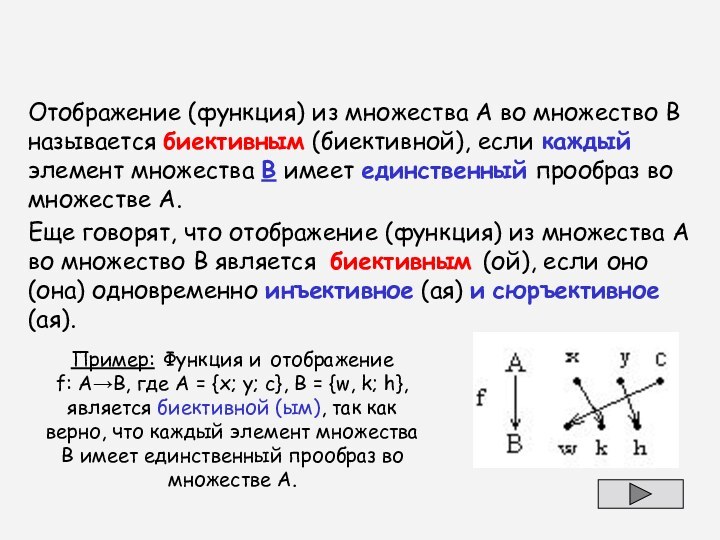
Слайд 115
Отображение (функция) из множества А во множество В
называется биективным (биективной), если каждый элемент множества В имеет
единственный прообраз во множестве А.
Еще говорят, что отображение (функция) из множества А во множество В является биективным (ой), если оно (она) одновременно инъективное (ая) и сюръективное (ая).
Пример: Функция и отображение f: АВ, где А = {х; у; с}, В = {w, k; h}, является биективной (ым), так как верно, что каждый элемент множества В имеет единственный прообраз во множестве А.
Слайд 116
Понятие бинарного отношения
Бинарным отношением , заданным на множестве
А, называется любое соответствие из множества А во множество
А, т.е. любое подмножество декартова произведения множеств АА.
- «тау»
Обозначение: АА, : А А.
(х;у) ху – х вступает в отношение с у.
(х;у) ху – х не вступает в отношение с у.
Слайд 117
СПОСОБЫ ЗАДАНИЯ
БИНАРНЫХ ОТНОШЕНИЙ
1. Указание характеристического свойства
2. Перечисление
упорядоченных пар
3. Граф
4. График
5. Таблица
Слайд 118
Указание характеристического свойства
А = {1,2,3}
: А
А
= {(x;y)xA yА xy }
характеристическое
свойство
Указанием характеристического свойства можно задавать бинарное отношение как на конечном, так и на бесконечном множестве, если существует закономерность образования упорядоченных пар, из которых оно состоит.
Слайд 119
Перечисление упорядоченных пар
=
{(1;1), (1;2), (1;3), (2;2), (2;3), (3;3)}
Перечислением упорядоченных пар
можно задавать
бинарное отношение только на конечном множестве.
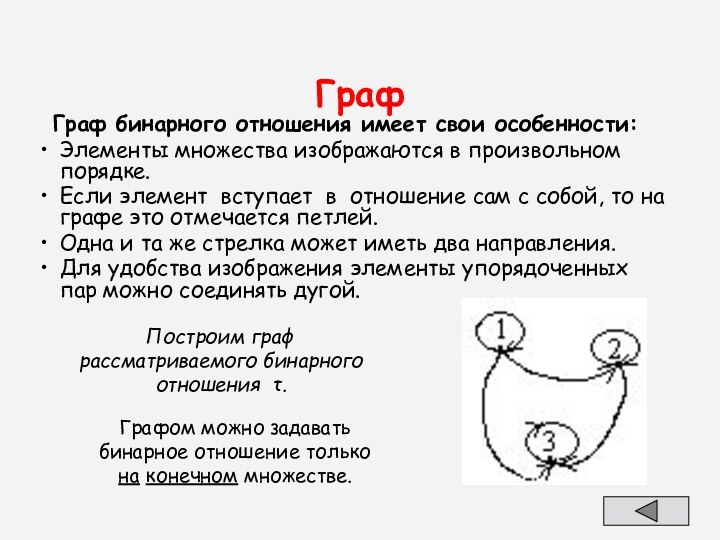
Слайд 120
Граф
Граф бинарного отношения имеет свои особенности:
Элементы
множества изображаются в произвольном порядке.
Если элемент вступает в отношение
сам с собой, то на графе это отмечается петлей.
Одна и та же стрелка может иметь два направления.
Для удобства изображения элементы упорядоченных пар можно соединять дугой.
Построим граф рассматриваемого бинарного отношения .
Графом можно задавать
бинарное отношение только
на конечном множестве.
Слайд 121
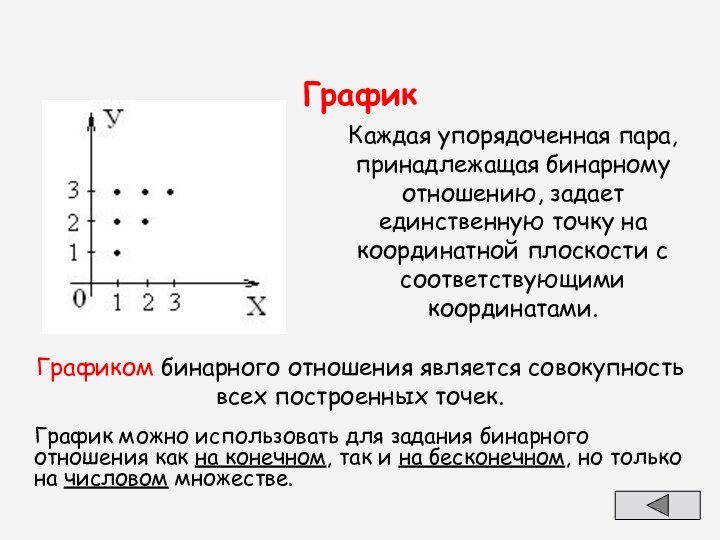
График
График можно использовать для задания бинарного отношения как
на конечном, так и на бесконечном, но только на
числовом множестве.
Каждая упорядоченная пара, принадлежащая бинарному отношению, задает единственную точку на координатной плоскости с соответствующими координатами.
Графиком бинарного отношения является совокупность всех построенных точек.
Слайд 122
Таблица
Если упорядоченная пара принадлежит бинарному отношению, то в
соответствующей клетке таблицы записывается 1, иначе – 0.
Таблицей можно
задавать бинарное отношение только
на конечном множестве.
Построим таблицу рассматриваемого бинарного отношения .
Слайд 123
Свойства бинарных отношений
Рефлексивность
Антирефлексивность
Симметричность
Антисимметричность
Транзитивность
Связность
Слайд 124
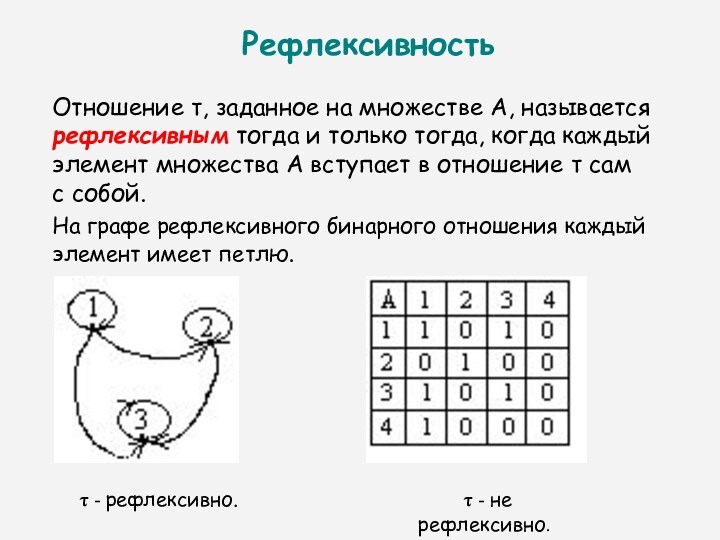
Рефлексивность
Отношение , заданное на множестве А, называется рефлексивным
тогда и только тогда, когда каждый элемент множества А
вступает в отношение сам с собой.
На графе рефлексивного бинарного отношения каждый элемент имеет петлю.
- рефлексивно.
- не рефлексивно.
Слайд 125
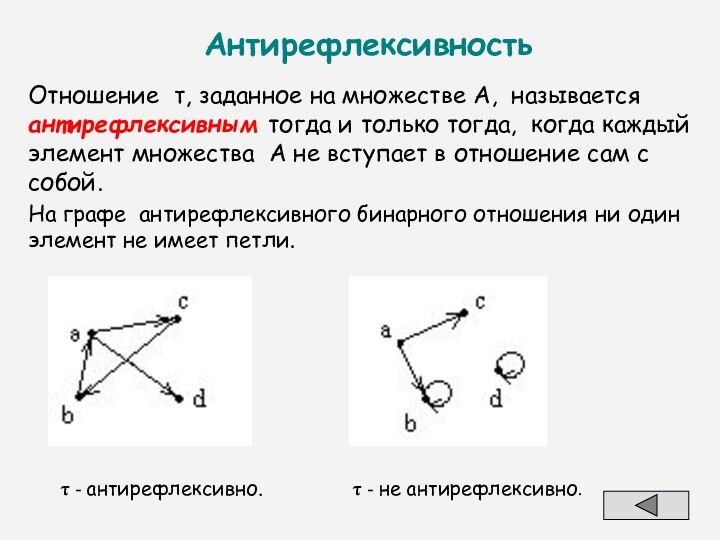
Отношение , заданное на множестве А, называется антирефлексивным
тогда и только тогда, когда каждый элемент множества А
не вступает в отношение сам с собой.
На графе антирефлексивного бинарного отношения ни один элемент не имеет петли.
Антирефлексивность
- антирефлексивно.
- не антирефлексивно.
Слайд 126
Симметричность
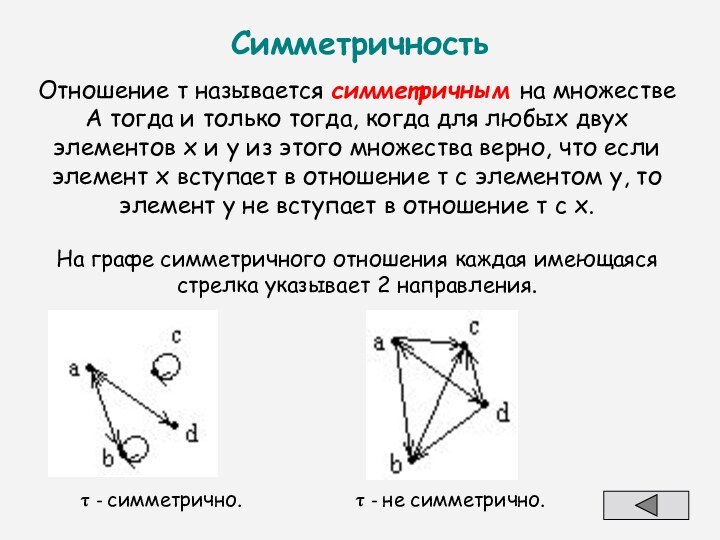
Отношение называется симметричным на множестве А тогда
и только тогда, когда для любых двух элементов х
и у из этого множества верно, что если элемент х вступает в отношение с элементом y, то элемент y не вступает в отношение с х.
На графе симметричного отношения каждая имеющаяся стрелка указывает 2 направления.
- симметрично.
- не симметрично.
Слайд 127
Антисимметричность
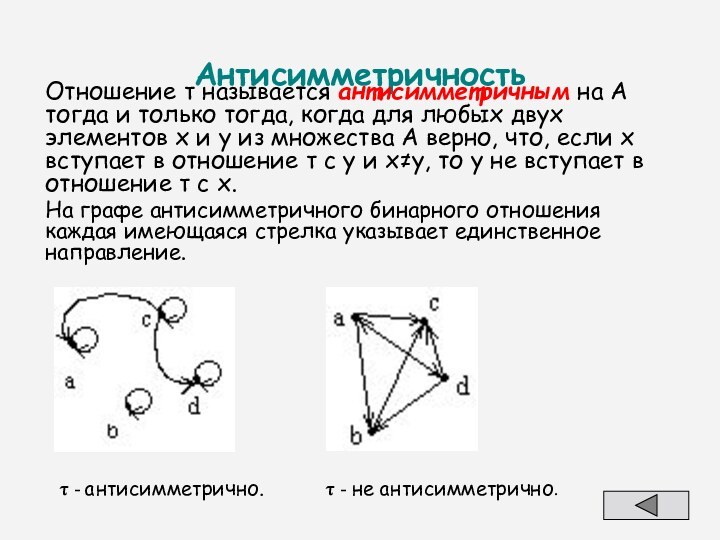
Отношение называется антисимметричным на А тогда и
только тогда, когда для любых двух элементов x и
y из множества А верно, что, если х вступает в отношение с у и ху, то у не вступает в отношение с х.
На графе антисимметричного бинарного отношения каждая имеющаяся стрелка указывает единственное направление.
- антисимметрично.
- не антисимметрично.
Слайд 128
Транзитивность
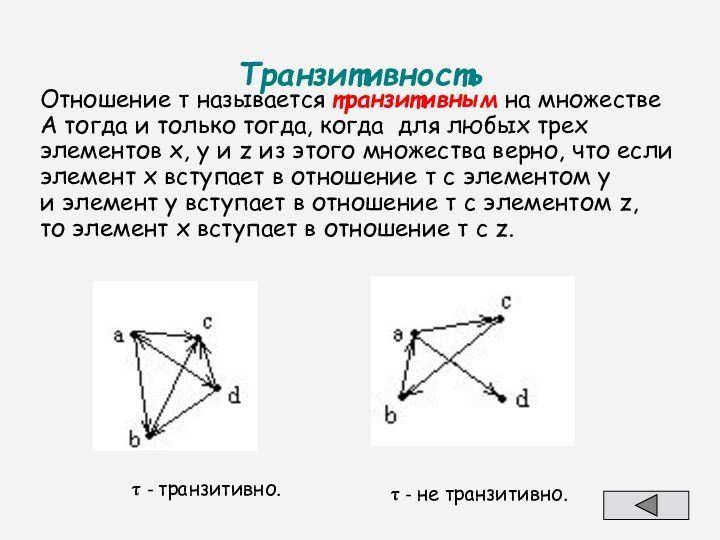
Отношение называется транзитивным на множестве А тогда
и только тогда, когда для любых трех элементов х,
у и z из этого множества верно, что если элемент х вступает в отношение с элементом y и элемент y вступает в отношение с элементом z, то элемент x вступает в отношение с z.
- транзитивно.
- не транзитивно.
Слайд 129
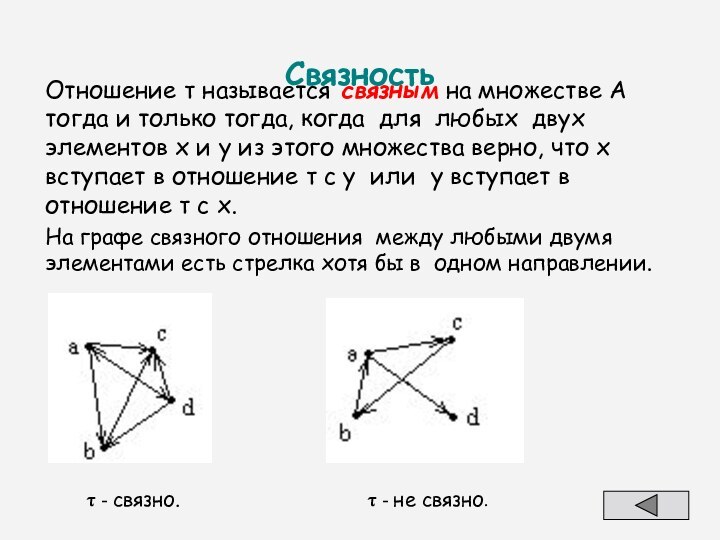
Связность
Отношение называется связным на множестве А тогда
и только тогда, когда для любых двух элементов x
и y из этого множества верно, что x вступает в отношение с y или y вступает в отношение с x.
На графе связного отношения между любыми двумя элементами есть стрелка хотя бы в одном направлении.
- связно.
- не связно.
Слайд 130
Типы бинарных отношений
рефлексивное, симметричное и транзитивное.
рефлексивное, антисимметричное и
транзитивное.
антирефлексивное, антисимметричное и транзитивное.
Слайд 131
Бинарные отношения линейного порядка
Слайд 132
Тема. Предикаты. Операции над предикатами
Слайд 133
«Предикат» с английского переводится как сказуемое.
Формально предикатом
называется функция, аргументами которой могут быть произвольные объекты из
некоторого множества, а значения функции «истина» или «ложь».
Предикат можно рассматривать как расширение понятия высказывания.
Слайд 134
Пример. Вместо трех высказываний
"Маша любит
кашу"
"Даша любит кашу"
"Саша
любит кашу"
можно написать один предикат
"Икс любит кашу"
и договориться, что вместо неизвестного Икс могут быть либо Маша,
либо Даша, либо Саша.
Подстановка вместо Икс имени конкретного ребенка превращает
предикат в обычное высказывание.
Слайд 135
Логика предикатов, расчленяет элементарное высказывание на субъект (буквально
– подлежащее, хотя оно может играть и роль дополнения)
и предикат (буквально – сказуемое, хотя оно может играть и роль определения).
Слайд 136
Субъект – это то, о чем что-то утверждается
в высказывании, а предикат – это то, что утверждается
о субъекте.
Например, в высказывании «7 – простое число»,
«7» – субъект,
«простое число» – предикат.
Это высказывание утверждает, что «7» обладает свойством «быть простым числом».
Слайд 137
Одноместным предикатом , определенном на множестве М, называется
предложение с переменной, которое превращается в высказывание при замене
этой переменной на ее значение из множества М.
Примеры
Слайд 138
P(x):=“x – сталица России.”, где М – множество
всех городов .
S(x):=“2x=3” , где М=N.
X+4
Слайд 139
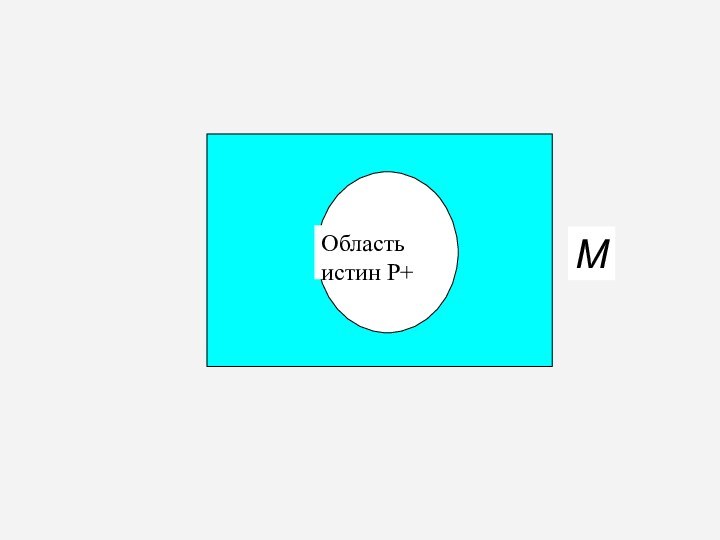
Множество M, на котором задан предикат, называется областью
определения предиката.
Множество , на котором предикат принимает только истинные
значения, называется областью истинности предиката Р(х).(Будем обозначать P+ )
Слайд 141
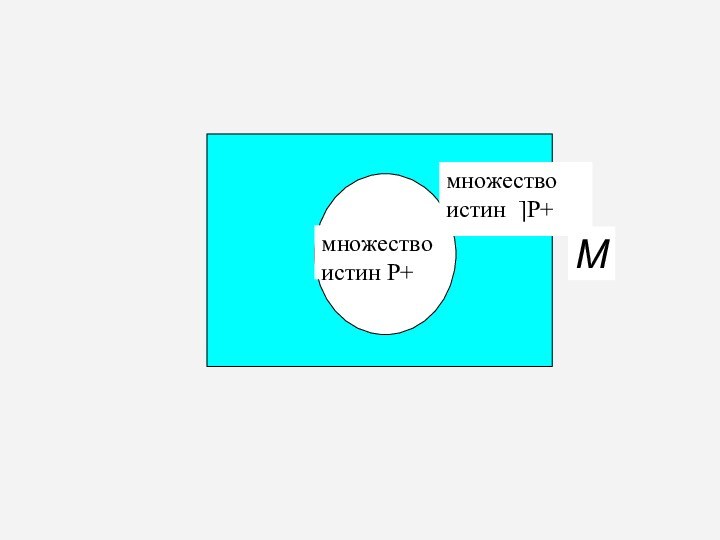
Предикат Р(х), определённый на множестве M, называется тождественно
истинным (тождественно ложным), если его область истинности совпадает с
М ( равна ).
Слайд 143
Определение . Двухместным предикатом P(x,у) называется функция двух
переменных х и у, определённая на множестве М=М1×М2 и
принимающая значения из множества {1,0}.
Слайд 144
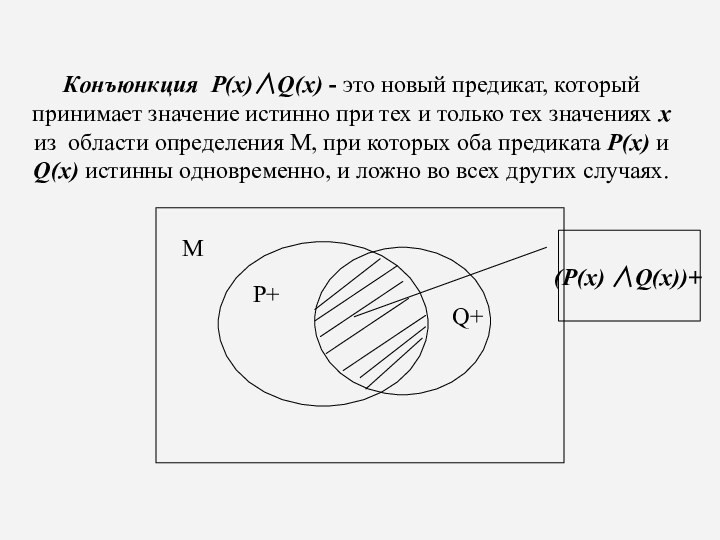
Конъюнкция P(x)Q(x) - это новый предикат, который принимает
значение истинно при тех и только тех значениях x
из области определения М, при которых оба предиката P(x) и Q(x) истинны одновременно, и ложно во всех других случаях.
М
Р+
Q+
(P(x) Q(x))+
Слайд 145
Дизъюнкция P(x)Q(x) - это новый предикат, который
принимает значение ложно при тех и только тех значениях
из области определения М, при которых оба предиката P(x) и Q(x) ложны одновременно, и истинно во всех других случаях.
P+
Q+
(P(x) Q(x))+
Слайд 146
Отрицание предиката P(x) -
это новый предикат, который принимает значение истинно при всех
x из из области определения М, при которых предикат P(x) принимает значение ложно и наоборот.
Слайд 148
. Над предикатами естественным образом вводятся также операции
импликации и эквиваленции.
Слайд 149
Переход от предиката Р(х) к высказыванию xР(х) ,
которое читается «для всех x имеет место Р(х) »
и считается истинным, если предикат P(x) превращается в истинное высказывание для любого значения x из области определения P(x), называется операцией навешивания квантора общности на предикат по переменной x.
букву называют квантором общности
Слайд 150
Переход от предиката Р(х) к высказыванию xР(х) ,
которое читается «существует такое x, что имеет место Р(х)
» и считается истинным, если предикат P(x) превращается в истинное высказывание хотя бы для одного значения x из области определения Р(х), называется операцией навешивания квантора существования на предикат по переменной x.
букву называют квантором общности
Слайд 151
Пусть на множестве натуральных чисел задан предикат P(x)
-«число кратно 3». высказывания:
xP(x) - «все натуральные числа кратны
3»;
xP(x)- «существуют натуральные числа, кратные 3».
Слайд 154
ГРУППЫ
Понятие группы является одним из важнейших понятий
современной математики.
Группы вездесущи: алгебра, геометрия, математический анализ, теоретическая
физика, теория линейных кодов, криптография, кристаллография – вот неполный перечень тех областей науки, где применяются группы.
Термин «группа» введен французским алгебраистом Э.Галуа (1811–1832) в 1832г.
При определении понятия группы используется понятие бинарной алгебраической операции. С уточнения этого интуитивно ясного понятия и начинается эта глава.
Слайд 155
§1. Бинарные алгебраические операции и их свойства
1. Понятие
бинарной алгебраической операции.
Простейшие операции над числами известны из
арифметики. К ним относятся, например, операции сложения, умножения, вычитания.
Общая черта, объединяющая эти операции, состоит в следующем: каждая из них любой паре чисел сопоставляет вполне определенное третье число.
При этом в случае операции вычитания разность двух неравных чисел зависит не только от самих этих чисел, но и от того, которое из них является уменьшаемым, а какое вычитаемым.
То есть результат операции зависит не только от того, к каким числам применяется операция, но и от того, в каком порядке эти числа берутся.
Таким образом, мы, по существу, пришли к определению алгебраической бинарной операции.
Слайд 156
§1. Бинарные алгебраические операции и их свойства
Определение. Бинарной
алгебраической операцией на множестве M называется любое отображение
: M M M декартового квадрата множества M в себя.
Т.о., операция любым двум элементам a и b из M, взятым в определенном порядке, ставит в соответствие единственный элемент c из M.
При этом пользуются записью a b = c и элемент c называют результатом операции , выполненной над элементами a и b;
сами элементы a и b называются компонентами операции .
Слайд 157
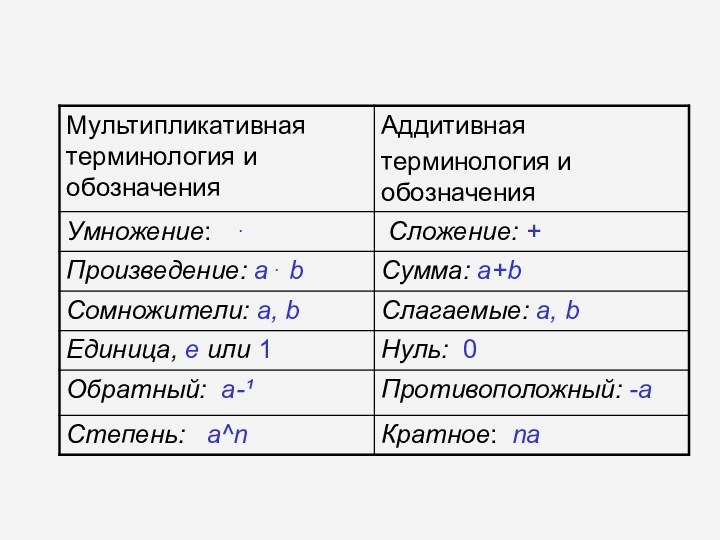
При изучении алгебраических структур бинарные операции зачастую называют
сложением или умножением и обозначают знаками + или
(иногда, чтобы не путать с арифметическим сложением или умножением, знаками или );
в первом случае говорят, что принята аддитивная терминология, во втором – мультипликативная терминология.
При аддитивной терминологии результат операции называют суммой, а компоненты – слагаемыми; при мультипликативной терминологии результат операции называют произведением, а компоненты – сомножителями.
В обычной математической практике для обозначения операций используют также символы ▪, •, , –, : , , , , и др.
Слайд 158
§1. Бинарные алгебраические операции и их свойства
В определении
бинарной алгебраической операции имеется требование, чтобы результат операции, выполненной
на любой паре элементов множества M , также принадлежал множеству M.
Это так называемый постулат замкнутости множества относительно бинарной алгебраической операции (или замкнутости операции).
С этой точки зрения нельзя считать бинарной алгебраической операцией, например, вычитание натуральных чисел или деление действительных чисел (деление на нуль невозможно).
Слайд 159
Перейдем теперь к примерам бинарных алгебраических операций.
Пример 1.
Обычное сложение и умножение на множествах N, Z, Q,
R являются бинарными алгебраическими операциями. ◙
Пример 2. Обычное вычитание является бинарной алгебраической операцией на множествах Z, Q, R. ◙
Пример 3. Обычное деление на множествах Q* =Q\{0}, R* =R\{0} рациональных, действительных чисел без нуля ◙
Слайд 160
Определение . Если во множестве M с операцией
истинна формула
x y = y x,
то
операция называется коммутативной.
Слайд 161
Определение . Если во множестве M с операцией
истинна формула
(x y) z = x
(y z),
то операция называется ассоциативной.
Слайд 162
Определение . Если во множестве M с операцией
существует такой элемент е, что истинна формула
x
e = e x = x,
то элемент е называется нейтральным относительно операции .
В случае аддитивной терминологии нейтральный элемент называют обычно нулем и обозначают символом 0.
В случае мультипликативной терминологии нейтральный элемент называют обычно единицей и обозначают символом е или 1.
Слайд 163
Нейтральным элементом относительно сложения во множествах Z, Q,
R является число 0;
Если во множестве M с операцией существует нейтральный
элемент e, то он единственный.
Слайд 165
Определение. Если во множестве M с операцией
и нейтральным элементом e для элемента а из Mсуществует
такой элемент а*, что справедливо равенство
a a* = a* a = e ,
то элемент а* называется симметричным к а относительно операции .
В случае аддитивной терминологии симметричный к а элемент называют противоположным и обозначают через –a;
в случае мультипликативной терминологии его называют обычно обратным и обозначают посредством а-1.
Во множестве M с ассоциативной операцией и нейтральным
элементом е каждый элемент обладает не более чем одним симметричным.
Слайд 167
Определение . Непустое множество G с определенной на
нем операцией называется группой, если в G истинны
аксиомы:
(G1) (x y) z = x (y z), т.е. операция ассоциативна;
(G2) ex(x e = e x = x), т.е. относительно операции существует нейтральный элемент e;
(G3) xx*(x x* = x* x = e) , т.е. каждый элемент из G обладает симметричным относительно операции .
Слайд 168
Примерами бесконечных групп являются числовые множества Z, Q,
R, относительно обычной операции сложения, и множества Q*, R*,
относительно умножения;
Слайд 170
Определение . Если на множестве заданы две операции
и , то говорят, что операция дистрибутивна
относительно операции , если в М справедливы тождества
(x y) z =(x z) (y z);
(x y) z =(x z) (y z).
Например, обычное умножение чисел дистрибутивно относительно сложения.
Слайд 171
Понятие кольца
Определение. Непустое множество K с определенными
на нем двумя операциями сложением и умножением называется кольцом,
если:
(К1) x + y = y + x, т.е. сложение коммутативно;
(К2) (x + y) + z = x + (y + z), т.е. сложение ассоциативно;
(К3) (x + 0 = 0 + x = x), т.е. относительно сложения существует нейтральный элемент;
(К4) (x + (–x) = 0), т.е. каждый элемент из обладает противоположным относительно сложения;
(К5) (x y) z = x (y z), т.е. умножение ассоциативно;
(К6) (x +y) z = (x z)+ (y z) и z (x +y) = (z x)+ (z y) , т.е. умножение дистрибутивно относительно сложения.
Слайд 172
§ 1. Понятие кольца и его простейшие свойства
Определение
2. Если умножение в кольце K коммутативно, т.е. в
K справедливо тождество
xy xy=yx,
то кольцо K называется коммутативным.
Определение 3. Если в кольце K есть единица относительно умножения, т.е. в K истинна формула
ex(xе = еx = x),
то кольцо K называют кольцом с единицей, или унитарным.
Слайд 173
Пример . Множества Z, Q, R, C относительно
обычных операций сложения и умножения являются коммутативными кольцами с
единицей. ◙


















































![Вводный курс математики Виды числовых промежутков- [a;b] – закрытый числовой промежуток от a до](/img/tmb/13/1252574/76ec5be71f8a9d20dde14e5c6bc8609f-720x.jpg)