- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ЗОЛОТОЕ СЕЧЕНИЕ
Содержание
- 2. ПЛАН РАБОТЫВВЕДЕНИЕПРОИСХОЖДЕНИЕ ЗОЛОТОЕ СЕЧЕНИЕ В КУЛЬТУРЕЗОЛОТОЕ СЕЧЕНИЕ В НАУКЕЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕВЫВОД / ЗАКЛЮЧЕНИЕЛИТЕРАТУРАПРИЛОЖЕНИЯ
- 3. ВВЕДЕНИЕЧеловек различает окружающие его предметы по форме.
- 4. ВВЕДЕНИЕВ математике пропорцией (proportio) называют равенство двух
- 5. ПРОИСХОЖДЕНИЕСчитается, что понятие о Золотом сечении ввел
- 6. КУЛЬТУРАВ эпоху Возрождения усиливается интерес к золотому
- 7. НАУКАРяд чисел 0, 1, 1, 2, 3,
- 8. ПРИРОДАФорма спирально завитой раковины привлекла внимание Архимеда.
- 9. ВЫВОДЗолотое сечение, не просто геометрическая пропорция, это
- 10. СПИСОК ЛИТЕРАТУРЫСвободная энциклопедия – Википедия.Лаврус В. И.
- 11. Комплекс дополнительных слайдов, для более подробного изучения.ПРИЛОЖЕНИЯ
- 12. ВВЕДЕНИЕ В ЗОЛОТОЕ СЕЧЕНИЕДАНОАВ = 1ВС =
- 13. ВТОРОЕ ЗОЛОТОЕ СЕЧЕНИЕБолгарский журнал «Отечество» опубликовал статью
- 14. ЗОЛОТОЙ ТРЕУГОЛЬНИКO – центр окружностиA – точка
- 15. ЗОЛОТОЙ ТРЕУГОЛЬНИКСтороны образуют угол 36° при вершине,
- 16. ПИРАМИДА ХЕОПСА
- 17. ПРОПОРЦИЯ ЧЕЛОВЕКАВ 1855 г. немецкий исследователь золотого
- 18. ПРОПОРЦИЯ ЧЕЛОВЕКАЗолотое сечение выражает средний статистический закон.Муж.
- 19. ПРОПОРЦИИ ЧЕЛОВЕКАЦейзинг дал определение золотому сечению, показал,
- 20. СЕЧЕНИЕ ФИБОНАЧИпри S = 0 из этой
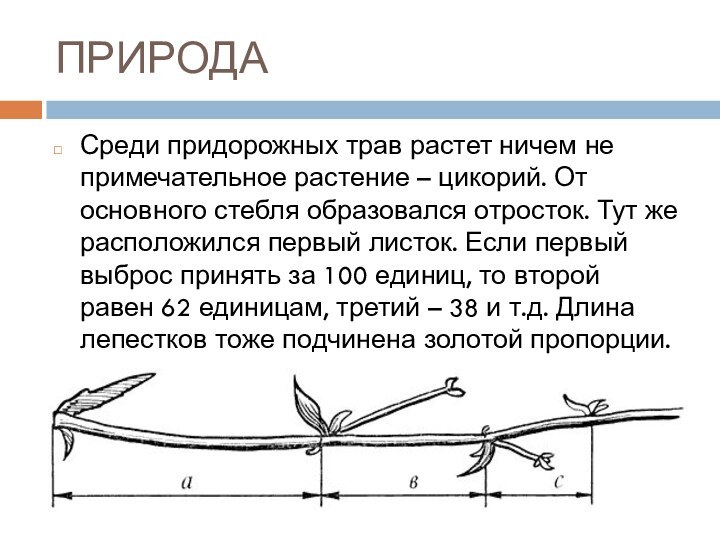
- 21. ПРИРОДАСреди придорожных трав растет ничем не примечательное
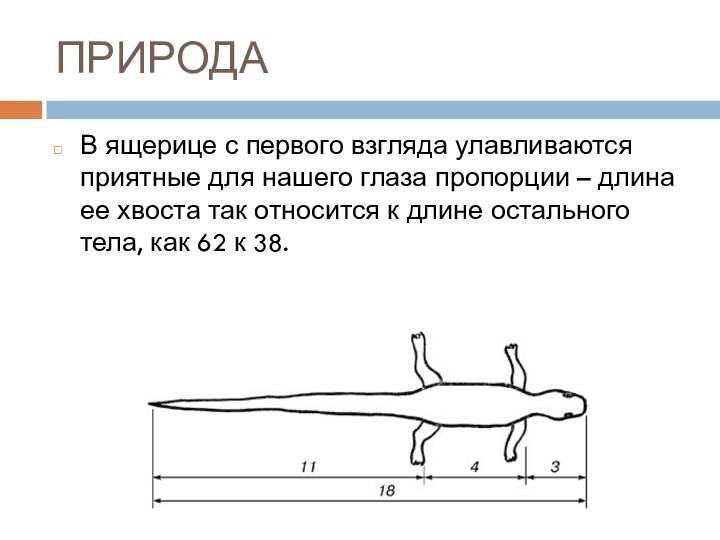
- 22. ПРИРОДАВ ящерице с первого взгляда улавливаются приятные
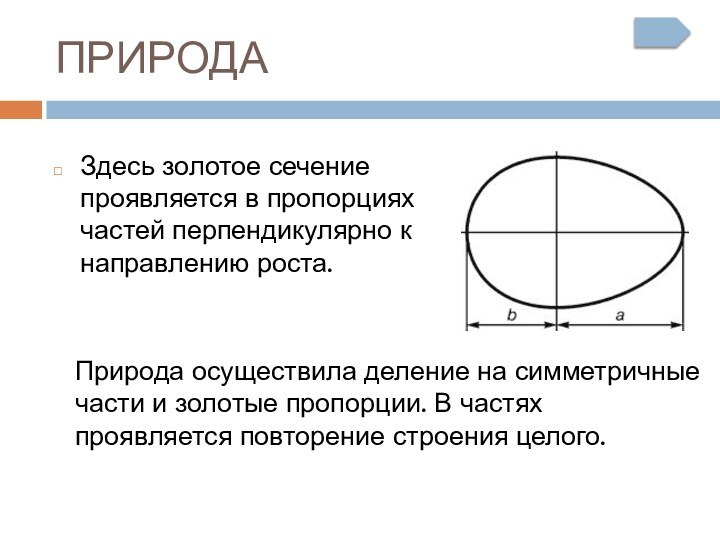
- 23. ПРИРОДАЗдесь золотое сечение проявляется в пропорциях частей
- 24. Скачать презентацию
- 25. Похожие презентации
ПЛАН РАБОТЫВВЕДЕНИЕПРОИСХОЖДЕНИЕ ЗОЛОТОЕ СЕЧЕНИЕ В КУЛЬТУРЕЗОЛОТОЕ СЕЧЕНИЕ В НАУКЕЗОЛОТОЕ СЕЧЕНИЕ В ПРИРОДЕВЫВОД / ЗАКЛЮЧЕНИЕЛИТЕРАТУРАПРИЛОЖЕНИЯ












Слайд 3
ВВЕДЕНИЕ
Человек различает окружающие его предметы по форме. Форма,
в основе построения которой лежат сочетание симметрии и золотого
сечения, способствует наилучшему зрительному восприятию. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому.Поэтому мы ставим перед собой цель – выявить обширность «Золотого сечения» и его значимость в Природе, Культуре и Науке.
Слайд 4
ВВЕДЕНИЕ
В математике пропорцией (proportio) называют равенство двух отношений:
a : b = c : d.
Золотое сечение –
это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей - a : b = b : c
Слайд 5
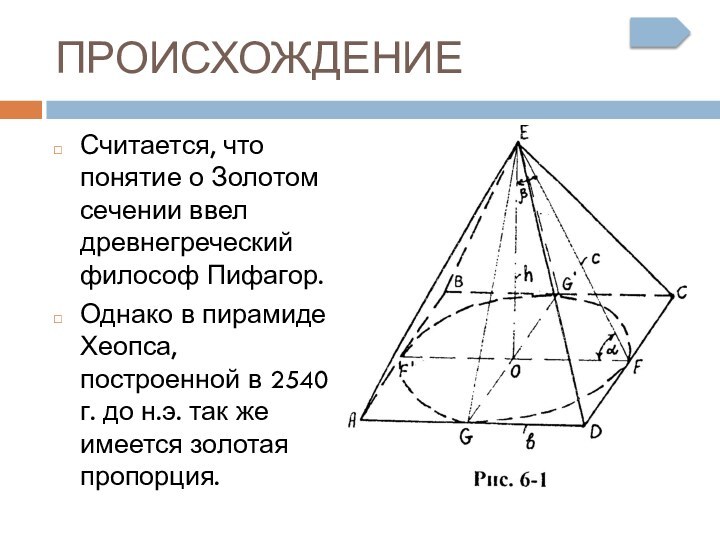
ПРОИСХОЖДЕНИЕ
Считается, что понятие о Золотом сечении ввел древнегреческий
философ Пифагор.
Однако в пирамиде Хеопса, построенной в 2540
г. до н.э. так же имеется золотая пропорция.
Слайд 6
КУЛЬТУРА
В эпоху Возрождения усиливается интерес к золотому делению
среди ученых и художников.
Да Винчи дал этому делению название
«золотое сечение» Таким образом Золотое сечение основательно проявило себя в культуре.
Слайд 7
НАУКА
Ряд чисел 0, 1, 1, 2, 3, 5,
8, 13, 21, 34, 55 и т.д. известен как
ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.
Слайд 8
ПРИРОДА
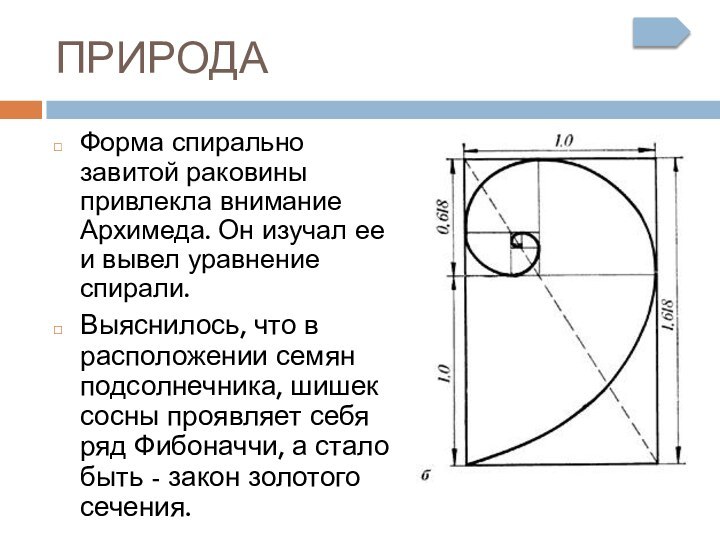
Форма спирально завитой раковины привлекла внимание Архимеда. Он
изучал ее и вывел уравнение спирали.
Выяснилось, что в
расположении семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть - закон золотого сечения.
Слайд 9
ВЫВОД
Золотое сечение, не просто геометрическая пропорция, это –
божественная константа, существующая независимо от нас, людей, и проявляясь
самым неожиданным образом в природе, живых организмах, науке, культуре и технике. У этой пропорции громадный спектр возможностей и использования, чему мы убедились во время этой работы.
Слайд 10
СПИСОК ЛИТЕРАТУРЫ
Свободная энциклопедия – Википедия.
Лаврус В. И. Измерения
в технике.
Прохоров А. И. Золотая спираль//Квант, 1984, №9
Пидоу Д.
Геометрия и искусство – Мир, 1979.Интернет.
Слайд 12
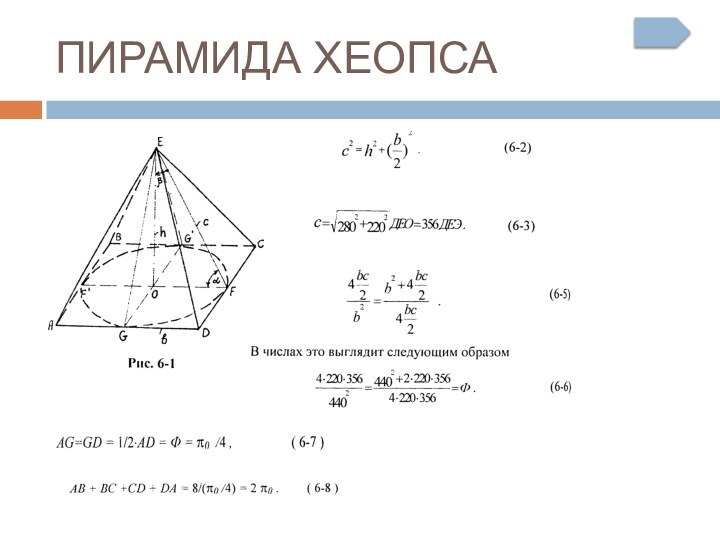
ВВЕДЕНИЕ В ЗОЛОТОЕ СЕЧЕНИЕ
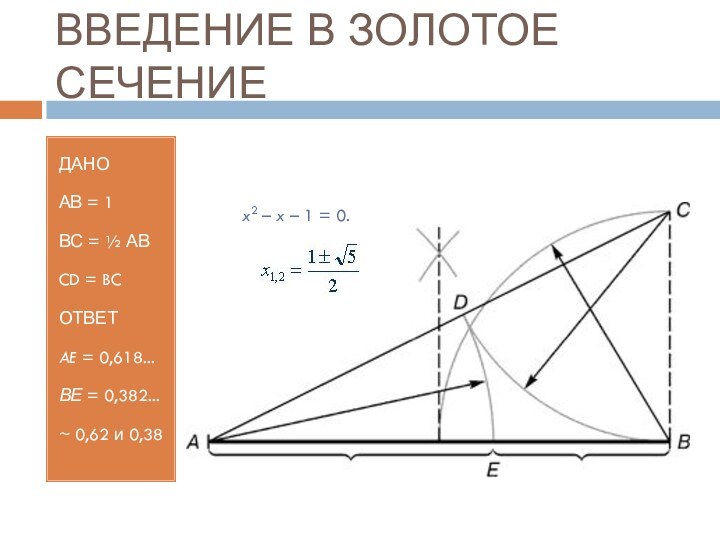
ДАНО
АВ = 1
ВС = ½
АВ
CD = BC
ОТВЕТ
AE = 0,618...
ВЕ = 0,382...
~ 0,62 и
0,38x2 – x – 1 = 0.
Слайд 13
ВТОРОЕ ЗОЛОТОЕ СЕЧЕНИЕ
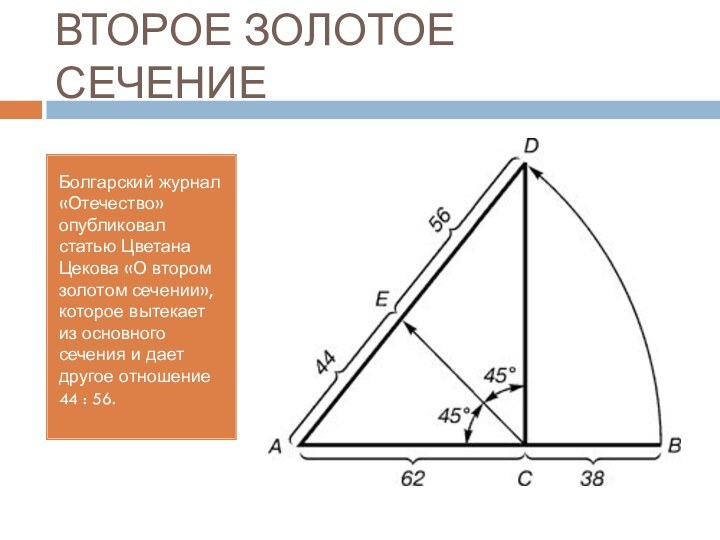
Болгарский журнал «Отечество» опубликовал статью Цветана
Цекова «О втором золотом сечении», которое вытекает из основного
сечения и дает другое отношение 44 : 56.
Слайд 14
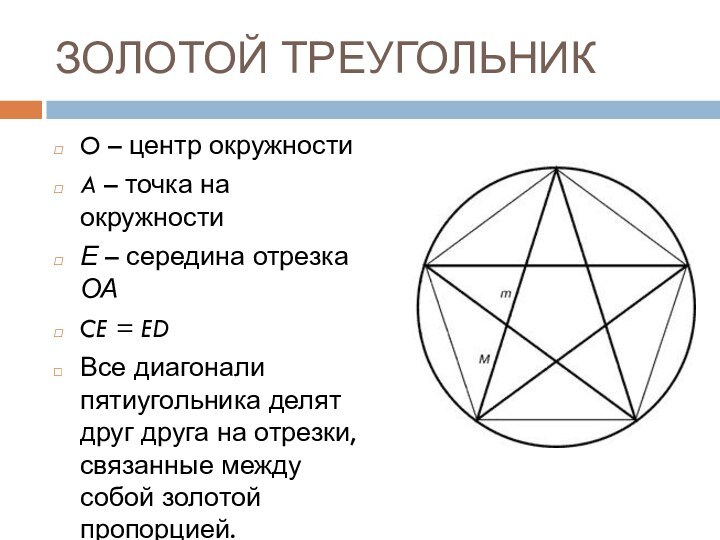
ЗОЛОТОЙ ТРЕУГОЛЬНИК
O – центр окружности
A – точка на
окружности
Е – середина отрезка ОА
CE = ED
Все диагонали
пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.
Слайд 15
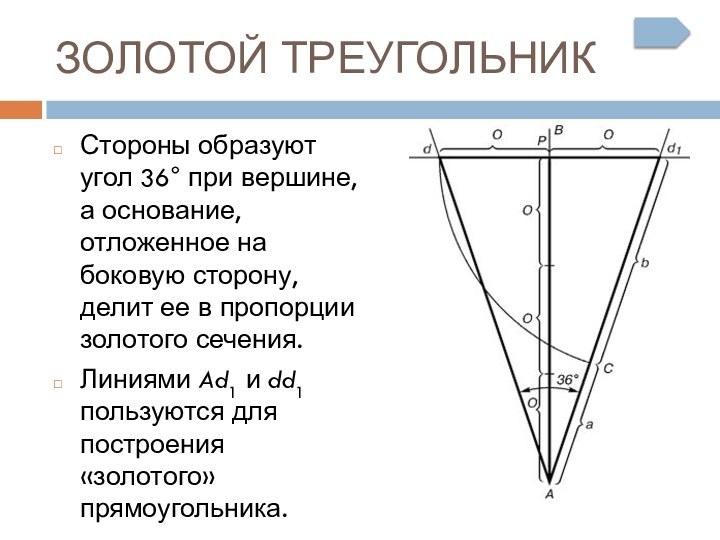
ЗОЛОТОЙ ТРЕУГОЛЬНИК
Стороны образуют угол 36° при вершине, а
основание, отложенное на боковую сторону, делит ее в пропорции
золотого сечения.Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.
Слайд 17
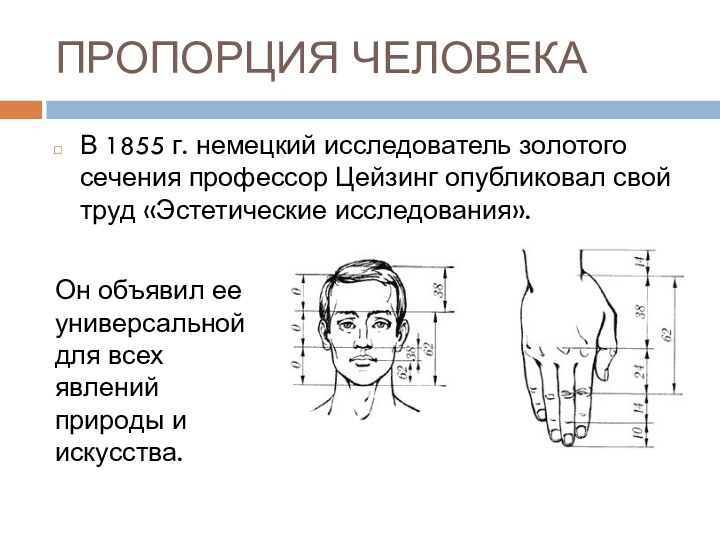
ПРОПОРЦИЯ ЧЕЛОВЕКА
В 1855 г. немецкий исследователь золотого сечения
профессор Цейзинг опубликовал свой труд «Эстетические исследования».
Он объявил ее
универсальной для всех явлений природы и искусства.
Слайд 18
ПРОПОРЦИЯ ЧЕЛОВЕКА
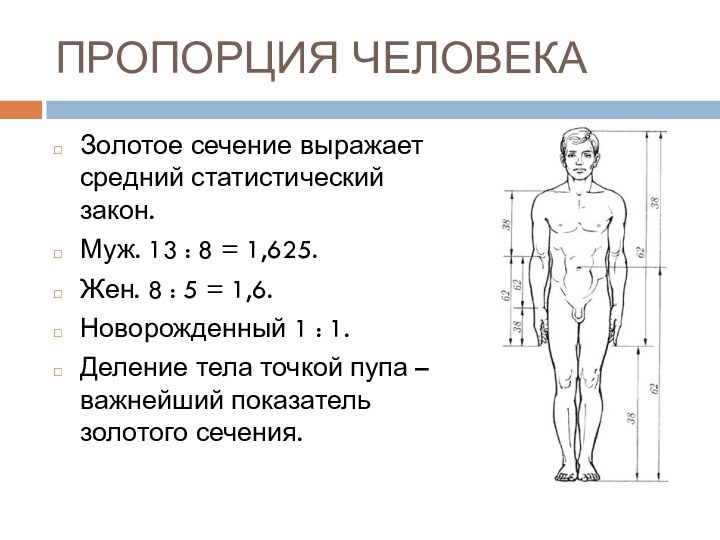
Золотое сечение выражает средний статистический закон.
Муж. 13
: 8 = 1,625.
Жен. 8 : 5 = 1,6.
Новорожденный
1 : 1.Деление тела точкой пупа – важнейший показатель золотого сечения.
Слайд 19
ПРОПОРЦИИ ЧЕЛОВЕКА
Цейзинг дал определение золотому сечению, показал, как
оно выражается в отрезках прямой и в цифрах. Когда
цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону.В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры.
Слайд 20
СЕЧЕНИЕ ФИБОНАЧИ
при S = 0 из этой формулы
мы получим «двоичный» ряд, при S = 1 –
ряд Фибоначчи, при S = 2, 3, 4. новые ряды чисел, которые получили название S-чисел Фибоначчи.В общем виде золотая S-пропорция есть положительный корень уравнения золотого S-сечения xS+1 – xS – 1 = 0.
В такой системе счисления любое натуральное число всегда представимо в виде конечной – а не бесконечной, как думали ранее!





























