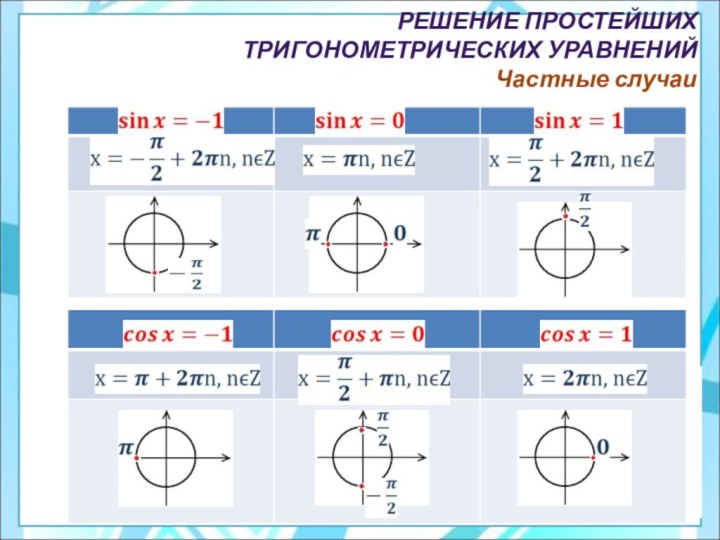
тригонометрических уравнений.
Закрепить навык решения тригонометрических уравнений.
Развитие умения анализировать, обобщать,
работать в группах.