- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Элементы комбинаторики и теории вероятностей. Математическая регата
Содержание
- 2. На завтрак мы можем выбрать плюшку, кекс,
- 3. Сколько комбинаций можно составить из цифр 2,4,
- 5. Из пункта А в пункт В ведут
- 6. Всего 12 путей, безопасных – 3.Какова вероятность, что выбранный путь будет безопасен?
- 7. Сколькими способами можно разложить 5 разных писем по одному в 5-ть конвертов?
- 8. Среди 5 почтовых голубей два белых. Какова вероятность, что ваше письмо понесет домой белый голубь?
- 9. Мы столкнулись с произведением подряд идущих натуральных
- 10. Что больше и во сколько раз
- 11. Выбрать правильное определение. А. Перестановкой из
- 12. к!(п – к)!. п! к
- 13. Рп = п!ПерестановкиРазмещенияСочетания
- 14. Сколькими способами можно разместить за круглым
- 15. В регате участвуют 8 команд. Сколькими различными
- 16. Из 9 членов команды надо выбрать
- 18. 1) Из города А в город В
- 19. 4) В классе учатся 16 мальчиков и
- 22. Скачать презентацию
- 23. Похожие презентации
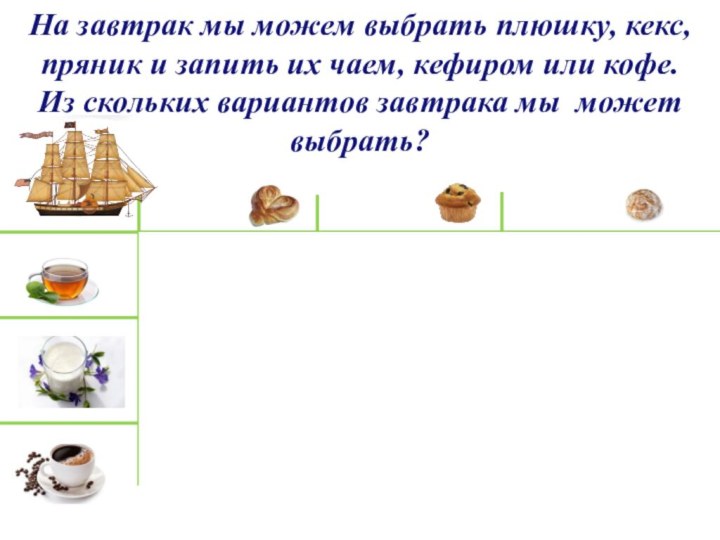
На завтрак мы можем выбрать плюшку, кекс, пряник и запить их чаем, кефиром или кофе. Из скольких вариантов завтрака мы может выбрать?




















Слайд 3 Сколько комбинаций можно составить из цифр 2,4, 5,
9, используя в записи числа каждую из них не
боле одного раза, чтобы открыть наш сейф?Слайд 5 Из пункта А в пункт В ведут 4
пути, а из пункта В в пункт С –
3 пути. Сколько путей, проходящих через В, ведут из А в С?А
В
С
Слайд 8 Среди 5 почтовых голубей два белых. Какова вероятность,
что ваше письмо понесет домой белый голубь?
Слайд 9 Мы столкнулись с произведением подряд идущих натуральных чисел.
Какое обозначение существует для такого произведения?
п! = 1 ·
2 · 3 · …· п.
Слайд 11
Выбрать правильное определение.
А. Перестановкой из п элементов
называется каждое расположение этих элементов в определённом порядке.
В.
Сочетанием из п элементов по к (к ≤ п) называется любое множество, состоящее из любых к элементов, взятых в определённом порядке из данных п элементов.С. Размещением из п элементов по к называется любое множество, составленное из к элементов, выбранных из п элементов.
Сочетанием из п элементов по к
Размещением из п элементов по к
Слайд 15 В регате участвуют 8 команд. Сколькими различными способами
могут быть распределены 3 различные медали?
3
8
8
3
8
?
8!
5!
=
=
=336
Слайд 16 Из 9 членов команды надо выбрать 3-х
дежурных. Сколькими способами можно сделать этот выбор?
9
3
9
3
3
9
=
=
=
=
=
=
=84
Слайд 18 1) Из города А в город В ведут
3 дороги, из города В в С – 2
дороги, из С в Д – 4 дороги. Сколькими способами можно проехать из города А в город Д через города В и С?А. 3·2·4=24 сп; Б. 3+2+4=9 сп; С. Другое решение.
2) Курьер должен разнести пакеты в 8 различных учреждений. Сколько маршрутов может он выбрать?
А. 1 + 2 + 3 + …+ 8; В. 8! С. Другое решение.
3) Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать 2-х для участия в олимпиаде по математике и русскому языку?
А В С.
Р30
Немного из истории комбинаторики
Слайд 19 4) В классе учатся 16 мальчиков и 12
девочек. Для уборки территории требуется выделить 4 мальчика и
3 девочки. Сколькими способами можно это сделать?А. С164 + С123; В. С164 · С123; С. Другое решение.
5) Сколько различных стартовых 6-к можно образовать из числа 10 волейболистов?
А. С106; В. А106; С. Другое решение.
Слайд 21
Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами можно это сделать?