3)
4)sin(-x)=-sin x
5)Возрастает на
Убывает
на 6)Периодичная
I вариант
y=sin x
II вариант
y=cos x
III вариант
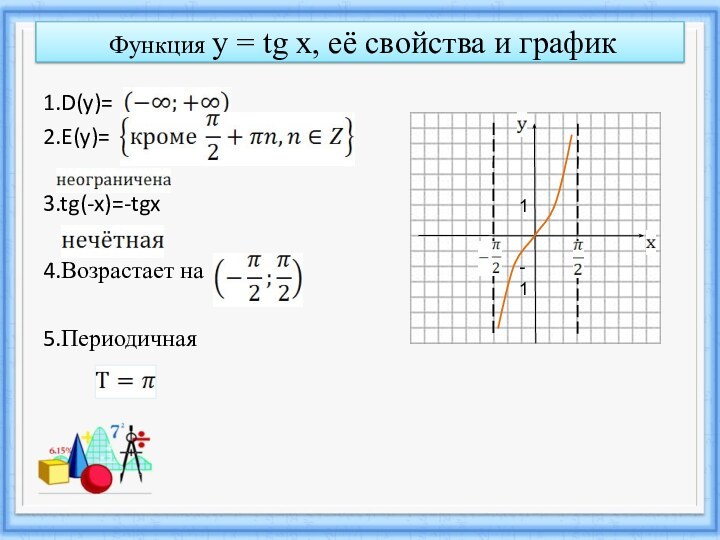
y=tg x
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть








![Обратные тригонометрические функции прямаяy=sin xD(y)=E(y)=обратнаяу=D(y)=E(y)=[-1;1][-1;1]arcsin xГрафики симметричны относительно прямой у=х - ось симметрии](/img/tmb/12/1142664/969fab19c13f636c0eae352a37f1e915-720x.jpg)
![Обратные тригонометрические функции 1. D(х) = [-1;1].2. Е(х) = -;.3. Функция является нечетной: arcsin](/img/tmb/12/1142664/3187290e5f21acd03abf40904fe11ebe-720x.jpg)





I вариант
y=sin x
II вариант
y=cos x
III вариант
y=tg x
1
-1
Ответ: нет, так как не везде выполняется условие монотонности
3.На каком промежутке монотонна функция синуса?
Ответ: возрастает и принимает значение [-1;1].
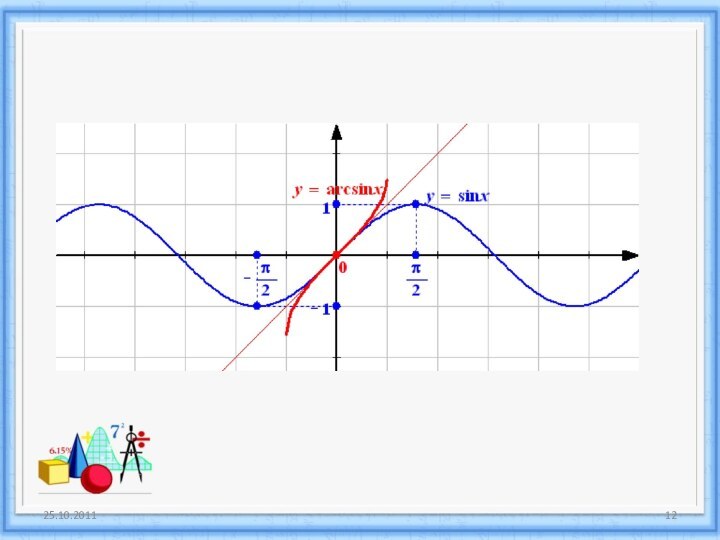
Свойства функции у= arssin x
1. Группа у= cos x
2. Группа у= tg x
3. Группа у= ctg x