Слайд 2
Пояснительная записка
В результате изучения курса математики учащиеся должны
понимать, что функция – математическая модель, позволяющая описывать и
изучать разнообразные зависимости между реальными величинами, уметь логически мыслить, проявлять творческие способности на уровне, необходимом для продолжения образования и для самостоятельной деятельности.
Данные дидактические материалы рассчитаны для курса математики 10 класса, обучающего по учебнику Алимов Ш.А. «Алгебра и начала анализа» по основной программе с учетом стандартов основного общего образования по математике.
Слайд 3
После пройденного курса учащиеся должны знать:
Определение области
определения и множества значений функции, в том числе тригонометрических
функций;
Определение четности и нечетности функции, периодичности тригонометрических функций;
Понятие функции косинуса, схему исследования функции y = cos (x) и её свойства;
Понятие функции синуса, схему исследования функции y = sin (x) и её свойства;
Понятие функции тангенса и котангенса, схему исследования функции y = tg (x) и y = ctg (x) и их свойства;
Какие функции являются обратными тригонометрическими, иметь представление об их графиках и свойствах.
Слайд 4
После изучения практического материала учащиеся должны уметь:
Находить область
определения и область значений тригонометрических функций;
Находить период тригонометрических функций,
исследовать их на четность и нечетность;
Строить графики функций y = cos (x), y = sin (x), y = tg (x) и
y = ctg (x);
Находить по графикам промежутки возрастания и убывания, промежутки постоянных знаков, наибольшее и наименьшее значения функций;
Преобразование графиков: параллельный перенос, симметрия относительно начала и осей координат, растяжение и сжатие вдоль осей координат;
Решать задачи с использованием свойств обратных тригонометрических функций;
Использовать свойства функции для сравнения и оценки её значений.
Слайд 5
§ 38. «Область определения и множество значений тригонометрических
функций».
Цель:
Знать: Определение области определения и множества значений функции, в
том числе тригонометрических функций.
Уметь: Находить область определения и область значений тригонометрических функций.
Урок 1-3.
Справочный материал:
Слайд 6
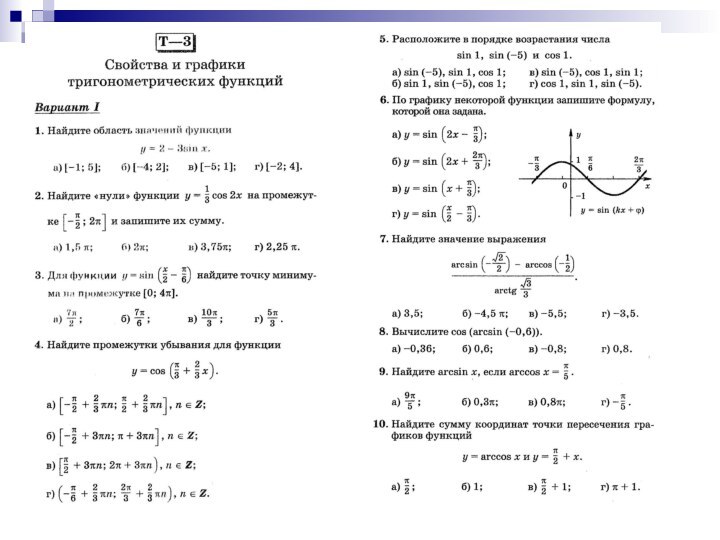
Тренировочный тест
1. Найдите область определения функции y =
√cos (x).
а) ;
б) ; в) ;
г) .
2. Найдите множество значений функции y = 3 - 5∙sin(x).
а) [-8; 8]; б) [-2; 8]; в) [-2; 5]; г) [-5; 2].
3. Чему равно наименьшее значение функции
y = sin (x) ∙ cos (x)?
а) -1; б) -2; в) -1/2; г) 1.
4. Чему равно наибольшее значение функции
y = sin2x – cos2x?
а) 0; б) 1; в) -1; г) 2.
Слайд 7
Тренажер №1
Найти область определения функции:
Слайд 8
Самостоятельная работа
1. Найдите область определения функции:
а)
а)
б) б)
в) в)
2. Найдите множество значений функции:
y = (cos x – sin x)2 y = (cos x + sin x)2
Слайд 9
§ 39. «Четность, нечетность, периодичность тригонометрических функций».
Цель:
Знать: Определение
четности и нечетности функции, периодичности тригонометрических функций.
Уметь: Находить период
тригонометрических функций, исследовать их на четность и нечетность.
Справочный материал:
Слайд 10
Тренировочный тест.
1. Какая из функций является четной?
А.
Б. В. Г.
2. Какая из функций является нечетной?
А. Б. В. Г.
3. Какая из функций не является четной, не является нечетной?
А. Б. В. Г.
4. Найдите наименьший положительный период функции
А. Б. В. Г.
5. Какая из функций имеет период 2П?
А. Б. В. Г.
Слайд 11
Диктант
В – 1
1. Функция f(x) периодическая с периодом
8. Запишите вытекающее отсюда равенство.
2. Каков наименьший положительный период
функции y=tg x ?
3. Является ли число 3,14 периодом синуса?
4. Каков наименьший положительный период функции
5. Каков наименьший положительный период функции
В – 2
1. Функция g(x) периодическая с периодом 6. Запишите вытекающее отсюда равенство.
2. Каков наименьший положительный период функции y=cos x ?
3. Является ли число 3,14 периодом котангенса?
4. Каков наименьший положительный период функции
5. Каков наименьший положительный период функции
Слайд 14
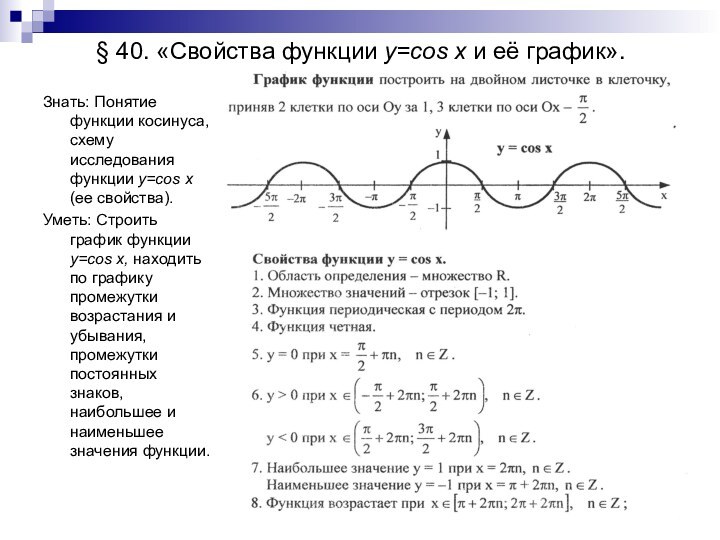
§ 40. «Свойства функции y=cos x и её
график».
Знать: Понятие функции косинуса, схему исследования функции y=cos x
(ее свойства).
Уметь: Строить график функции y=cos x, находить по графику промежутки возрастания и убывания, промежутки постоянных знаков, наибольшее и наименьшее значения функции.
Слайд 15
Самостоятельная работа
В – 1.
1. Изобразите схематически график функции
y=3∙cos(x). Отметьте на графике три точки, для которых у=1,5.
Чему равны соответствующие значения х?
2. Запишите наименьший положительный период функции .
3. Запишите промежутки возрастания и убывания функции .
4. Для функции найдите:
а) область определения; б) множество значений; в) нули функции.
В – 2.
1. Изобразите схематически график функции .
Отметьте на графике три точки, для которых у=-0,5. Чему равны соответствующие значения х?
2. Запишите наименьший положительный период функции y=0,5∙cos(0,5x).
3. Найдите, в каких точках функция y=3∙cos(x) – 2 достигает своего наибольшего значения?
4. Начертите график функции y=cos(x) на отрезке [-Π; 2,5Π]. Отметьте на этом графике множество точек, для которых выполняются условия: а) cos(x) = 1;
б) cos(x) > 0,5. Выпишите соответствующие значения х, при которых выполняется каждое из условий.
Слайд 16
§ 41. «Свойства функции y=sin x и её
график».
Знать: понятие функции синуса, схему исследования функции y=sin x
(ее свойства).
Уметь: Строить график функции y=sin x, находить по графику промежутки возрастания и убывания, промежутки постоянных знаков, наибольшее и наименьшее значения функции.
Слайд 17
Проверочная работа
В – 1.
1. Изобразите схематически график функции
y = sin(x). Отметьте на графике три точки, для
которых у = 1. Чему равны соответствующие значения х?
2. Запишите промежутки возрастания и убывания функции на отрезке
В – 2.
1. Запишите наименьший положительный период функции .
2. Найдите наибольшие и наименьшие значения функции .
3. Сравните числа sin1 и sin3.
В – 3.
Для функции y = 2∙sin(3x) найдите:
а) область определения; б) множество значений; в) нули функции; г) промежутки знакопостоянства; д) наибольшее и наименьшее значения; е) промежутки возрастания и убывания. Постройте этот график.
В – 4.
Начертите график функции y = sin(x) на отрезке [-Π; 2,5Π]. Отметьте на этом графике множество точек, для которых выполняются условия: а) sin(x) = 1; б) sin(x) = 0,5;
в) sin(x) > 0,5. Выпишите соответствующие значения х, при которых выполняется каждое из условий.
Слайд 18
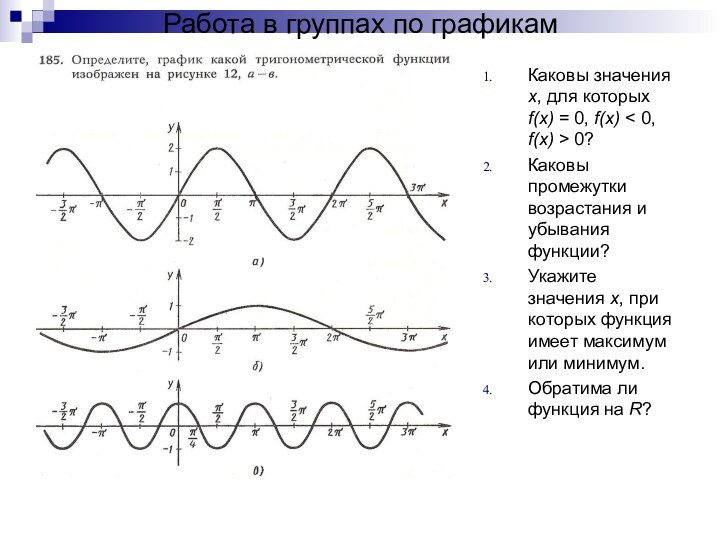
Работа в группах по графикам
Каковы значения х, для
которых f(x) = 0, f(x) < 0, f(x) >
0?
Каковы промежутки возрастания и убывания функции?
Укажите значения х, при которых функция имеет максимум или минимум.
Обратима ли функция на R?
Слайд 19
Тренировочная работа
1. Для функции y = sin(x) укажите
на отрезке [0; 2Π] промежутки, в которых эта функция:
а) возрастает;
б) убывает; в) положительна; г) отрицательна.
2. При каких значениях х на [0; 2Π) функция принимает наибольшее значение и чему оно равно:
а) y = 3 + cos(x); б) y = 2 - sin(x)?
3. При каких значениях х на [0; 2Π) функция принимает наименьшее значение и чему оно равно:
а) y = 3 + cos(x); б) y = 2 - sin(x)?
4. Существует ли такое значение х из интервала (0; Π), при котором функция y = tg(x) принимает своё наибольшее значение?
Слайд 20
Диктант
В – 1 [ В – 2 ].
Какова
область определения [значений] синуса?
Какова область значений [определения] тангенса?
Является ли
функция y = cos(x) [y = tg(x)] нечетной?
Каков наименьший положительный период функции
y = tg(x) [y = sin(x)] ?
Укажите нули функции y = sin(x) [y = tg(x)].
Укажите промежутки, на которых тангенс положителен
[косинус отрицателен].
Выяснить возрастает или убывает функция y = cos(x)
[y = sin(x)] на промежутке .
Слайд 21
Тренажер №3
Постройте график функции:
Слайд 22
§ 42. «Свойства функции y = tg (x)
и её график».
Знать: понятие функции тангенса, схему исследования функции
y = tg (x) (ее свойства); понятие функции котангенса, схему исследования функции y = ctg (x) (ее свойства).
Уметь: строить графики функций y = tg (x), y = ctg (x), находить по графику промежутки возрастания и убывания, промежутки знакопостоянства, наибольшие и наименьшие значения функции.
Слайд 25
§ 43. «Обратные тригонометрические функции».
Знать: какие функции являются
обратными тригонометрическими, иметь представление об их графиках, свойствах.
Уметь: решать
задачи с использованием свойств обратных тригонометрических функций.
Слайд 30
Контрольная работа
Тема: «Тригонометрические функции».
















![Основные тригонометрические функции Тренировочная работа1. Для функции y = sin(x) укажите на отрезке [0; 2Π]](/img/tmb/12/1180478/efecb6c39cf9098efc19438cd6103a8c-720x.jpg)
![Основные тригонометрические функции ДиктантВ – 1 [ В – 2 ].Какова область определения [значений] синуса?Какова](/img/tmb/12/1180478/3b7a4f6520cf3a3e7ae7fbcd9fc8f663-720x.jpg)