Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему по алгебре Логарифм и его свойства (10 класс)

Содержание

2. Три пути ведут к знанию: путь размышления
3. Логарифм и его свойства
4. Выберите и продолжите фразу : « Сегодня
5. Оценочный лист
6. Логарифмом числа b по основанию а называется
7. Логарифмом числа b по основанию а называется
8. 198 1 9 28 2Обгонялки
9. При каких значениях х существует логарифм
10. Основное логарифмическое тождество.Логарифм произведения.Логарифм частного.Логарифм степени.Формула перехода к новому основанию.В пустое окошко запишите формулу
11. Свойства логарифмов a>0,b>0,c>0, c≠1logaaloga1logca + logcblogca - logcblogc(ab)logc(a/b)alogablogabnnlogab01b
12. Свойства логарифмов a>0,b>0,c>0, c≠1logaaloga1logca + logcblogca - logcblogc(ab)logc(a/b)alogablogabnnlogab01b
13. Графический диктант
14. Ключ _;_;_;_;_;_;+;+;+
15. «Логарифмический дартс» составить логарифм с числами3,3,278,2,647,1,0
16. Готовимся к ЕГЭ
18. +3+5 : 322+3задания части В 1)Вычислить,если b = -2
19. Решая задачи, мы погружаемся в строгое пространство
20. Практическое применение логарифмовПодготовили Бельская Валерия и Сильченко Богдан
21. Логарифмические функции распространены чрезвычайно широко как в
22. Одним из наиболее наглядных примеров является логарифмическая
23. Раковины морских животных могут расти лишь в
24. Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. Биология
25. Механика и физикаПринцип Больцмана в статистической термодинамике — одна из
26. Единицей громкости звука служит «бел», практически -
27. АстрономияПо логарифмическим спиралям закручены и многие Галактики, в частности Галактика, которой принадлежит Солнечная система.
28. ГеографияРихтер предложил для оценки силы землетрясения (в его
29. Музыка«Ступени" темперированной хроматической гаммы не расставлены на
30. ИнформатикаПрименяется для вычисления основной единицы – бита.
33. Вычислить:
34. Подведение итогов
35. РефлексияНа уроке я работал
36. Домашнее заданиеНа «3» с.114 проверь себя №
37. Вы сегодня погрузились в логарифмы, Безошибочно их
38. Скачать презентацию
39. Похожие презентации

Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта – это путь самый горький. Конфуций

Главная
Алгебра
Презентация по алгебре Логарифм и его свойства (10 класс)

Три пути ведут к знанию: путь размышления – это путь самый благородный,

Выберите и продолжите фразу : « Сегодня на уроке мы…»Решать упражнения, применяя

Логарифмом числа b по основанию а называется показатель степени, в которую нужно

При каких значениях х существует логарифм Х > 3X< 10X <

Основное логарифмическое тождество.Логарифм произведения.Логарифм частного.Логарифм степени.Формула перехода к новому основанию.В пустое окошко запишите формулу

Свойства логарифмов a>0,b>0,c>0, c≠1logaaloga1logca + logcblogca - logcblogc(ab)logc(a/b)alogablogabnnlogab01b

«Логарифмический дартс» составить логарифм с числами3,3,278,2,647,1,0

Презентация по алгебре Логарифм и его свойства (10 класс)

+3+5 : 322+3задания части В 1)Вычислить,если b = -2

Решая задачи, мы погружаемся в строгое пространство чисел и не задумываемся о

Практическое применение логарифмовПодготовили Бельская Валерия и Сильченко Богдан

Логарифмические функции распространены чрезвычайно широко как в математике, так и в естественных

Одним из наиболее наглядных примеров является логарифмическая спираль. Спираль в одну сторону

Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком

Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмическим спиралям. Биология

Механика и физикаПринцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы, характеризующая

Единицей громкости звука служит «бел», практически - его десятая доля, «децибел». Разности

АстрономияПо логарифмическим спиралям закручены и многие Галактики, в частности Галактика, которой принадлежит Солнечная система.

ГеографияРихтер предложил для оценки силы землетрясения (в его эпицентре) десятичный логарифм перемещения (в микрометрах) иглы

ИнформатикаПрименяется для вычисления основной единицы – бита. Бит — это двоичный логарифм вероятности равновероятных событий

Домашнее заданиеНа «3» с.114 проверь себя № 1На «4» № 294, 296

Вы сегодня погрузились в логарифмы, Безошибочно их надо вычислять, На экзамене, конечно,

Слайды презентации

Слайд 2 Три пути ведут к знанию: путь размышления – это

Три пути ведут к знанию: путь размышления – это путь самый

путь самый благородный, путь подражания – это путь самый легкий

и путь опыта – это путь самый горький.

Конфуций

Слайд 3 Логарифм
и его свойства

Слайд 4 Выберите и продолжите фразу : « Сегодня на

Выберите и продолжите фразу : « Сегодня на уроке мы…»Решать упражнения,

уроке мы…»
Решать упражнения, применяя свойства логарифмов;
Решать текстовые задачи на

движение;
Упрощать логарифмические выражения;
Решать самостоятельно задания, используя свойства и определение логарифмов;
Решать логарифмические уравнения и неравенства

Слайд 5 Оценочный лист

Слайд 6 Логарифмом числа b по основанию а называется показатель

Логарифмом числа b по основанию а называется показатель степени, в которую

степени, в которую нужно возвести основание а, чтобы получить

число b.

Собери определение

Логарифмом

числа

по основанию

называется

показатель

степени

в которую

нужно

возвести

основание

а,

чтобы

получить

число

Слайд 7 Логарифмом числа b по основанию а называется показатель

степени, в которую нужно возвести основание а, чтобы получить

число b.

Собери определение

Логарифмом

числа

по основанию

называется

показатель

степени

в которую

нужно

возвести

основание

а,

чтобы

получить

число

Слайд 9 При каких значениях х существует логарифм
Х

> 3
X< 10
X < 0
X
R
Не существует ни при

каком х

Слайд 10 Основное логарифмическое тождество.
Логарифм произведения.
Логарифм частного.
Логарифм степени.
Формула перехода к

новому основанию.
В пустое окошко запишите формулу

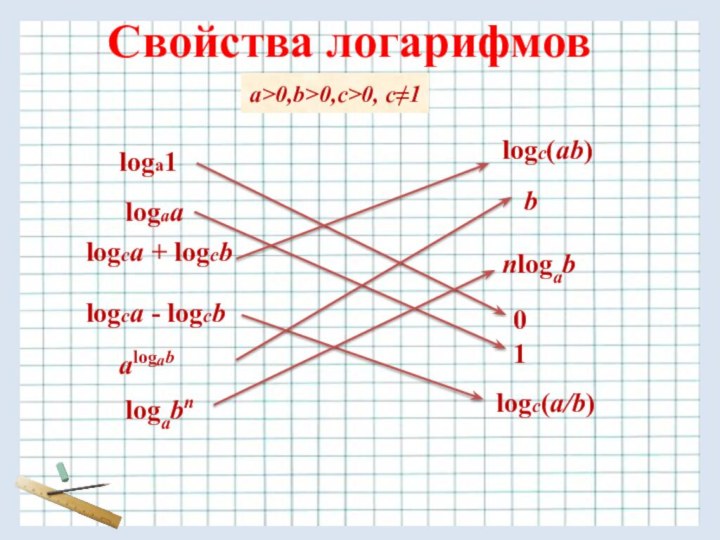
Слайд 11 Свойства логарифмов
a>0,b>0,c>0, c≠1
logaa
loga1
logca + logcb
logca - logcb
logc(ab)
logc(a/b)
alogab
logabn
nlogab
0
1
b

Слайд 12 Свойства логарифмов
a>0,b>0,c>0, c≠1
logaa
loga1
logca + logcb
logca - logcb
logc(ab)
logc(a/b)
alogab
logabn
nlogab
0
1
b

Слайд 13 Графический диктант

Слайд 14 Ключ _;_;_;_;_;_;+;+;+

Слайд 15 «Логарифмический дартс» составить логарифм с числами
3,3,27
8,2,64
7,1,0

Слайд 16 Готовимся к ЕГЭ

Слайд 18
+
3+5

:

32
2+3
задания части В
1)Вычислить

,если

b = -2

Слайд 19 Решая задачи, мы погружаемся в строгое пространство чисел

Решая задачи, мы погружаемся в строгое пространство чисел и не задумываемся

и не задумываемся о том, что математическое пространство тесно

связано с природой и практической жизнью человека Вы дома работали над вопросами: Где можно встретить логарифмы? Для чего они необходимы?

Слайд 20 Практическое применение
логарифмов
Подготовили Бельская Валерия и Сильченко Богдан

Слайд 21 Логарифмические функции распространены чрезвычайно широко как в математике,

Логарифмические функции распространены чрезвычайно широко как в математике, так и в

так и в естественных науках.
Ряд явлений природы помогает

описать логарифмическая зависимость. Иначе говоря, математики, пытаясь составить математическую модель того или иного явления, достаточно часто обращаются именно к логарифмической функции.

Слайд 22 Одним из наиболее наглядных примеров является логарифмическая спираль.

Одним из наиболее наглядных примеров является логарифмическая спираль. Спираль в одну

Спираль в одну сторону развертывается до бесконечности, а вокруг

полюса, напротив, закручивается, стремясь к нему, но не достигая.

Слайд 23 Раковины морских животных могут расти лишь в одном

Раковины морских животных могут расти лишь в одном направлении. Чтобы не

направлении. Чтобы не слишком вытягиваться в длину, им приходится

скручиваться, причем рост совершается так, что сохраняется подобие раковины с её первоначальной формой. А такой рост может совершаться лишь по логарифмической спирали.

Биология

Слайд 24 Один из наиболее распространенных пауков, эпейра, сплетая паутину,

закручивает нити вокруг центра по логарифмическим спиралям.
Биология

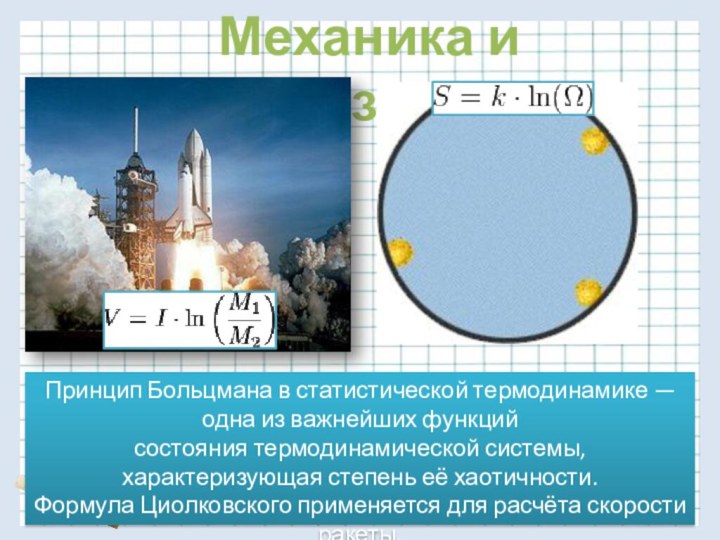
Слайд 25 Механика и физика
Принцип Больцмана в статистической термодинамике — одна из важнейших

Механика и физикаПринцип Больцмана в статистической термодинамике — одна из важнейших функций состояния термодинамической системы,

функций состояния термодинамической системы, характеризующая степень её хаотичности.
Формула Циолковского применяется для

расчёта скорости ракеты.

Слайд 26 Единицей громкости звука служит «бел», практически - его

Единицей громкости звука служит «бел», практически - его десятая доля, «децибел».

десятая доля, «децибел». Разности громкостей в 1 бел отвечает

отношение силы шумов 10. Значит, громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.

Слайд 27 Астрономия
По логарифмическим спиралям закручены и многие Галактики, в

частности Галактика, которой принадлежит Солнечная система.

Слайд 28 География
Рихтер предложил для оценки силы землетрясения (в его эпицентре) десятичный

ГеографияРихтер предложил для оценки силы землетрясения (в его эпицентре) десятичный логарифм перемещения (в микрометрах)

логарифм перемещения (в микрометрах) иглы стандартного сейсмографа Вуда-Андерсона, расположенного на расстоянии не

более 600 км от эпицентра.

Слайд 29 Музыка
«Ступени" темперированной хроматической гаммы не расставлены на равных

расстояниях ни по отношению к числам колебаний, ни по

отношению к длинам волн соответствующих звуков, а представляют собой логарифмы этих величин. Отсюда видим, что номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков.