- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку по математике Числовые функции
Содержание
- 2. "Числа не Боги, они не управляют миром,
- 3. Эпиграфом нашего урока являются слова А. Эйнштейна:
- 4. Цели урока: 1. Обобщить
- 5. РазминкачетнаянечетнаяалгебрафункцияспьФункция, график которой симметричен относительно оси Оу.Функция,
- 6. Свойства функций (исследование функции)Область определения функции;Промежутки монотонности;Ограниченность функции;Наибольшее, наименьшее значения функции;Непрерывность функции;Выпуклость функции;Область значения функции.
- 7. Функция задана графиком.Укажите область определения этой функции.1
- 8. 1 2 3 4
- 9. 1 2 3 4
- 10. 1 2 3 4
- 11. 1 2 3 4
- 12. 1 2 3 4
- 13. Укажите график четной функции.4231ПОДУМАЙ!ПОДУМАЙ!Верно! График симметричен относительно оси ОуПОДУМАЙ!
- 14. Укажите график нечетной функции.3431ПОДУМАЙ!Это четная функция!ПОДУМАЙ!Верно! График симметричен относительно точки О
- 15. -4 -3 -2
- 16. -4 -3 -2
- 17. Ответы для самопроверкиВариант 1Вариант 2[7;9) [-3;5)
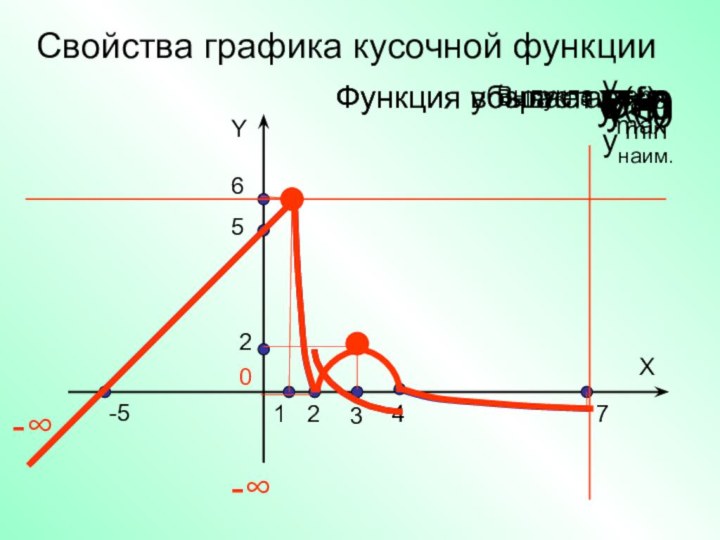
- 18. Построить и перечислить свойства графика кусочной функции
- 19. График функцииYX51-5
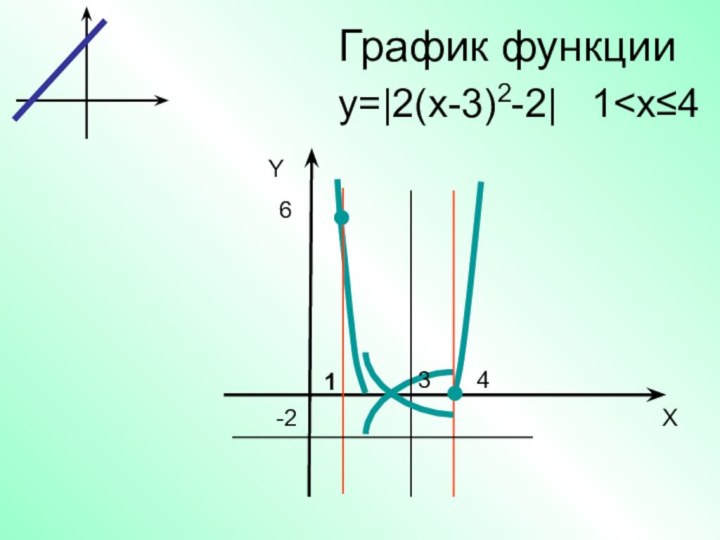
- 20. График функцииYX3-2641y=|2(x-3)2-2| 1
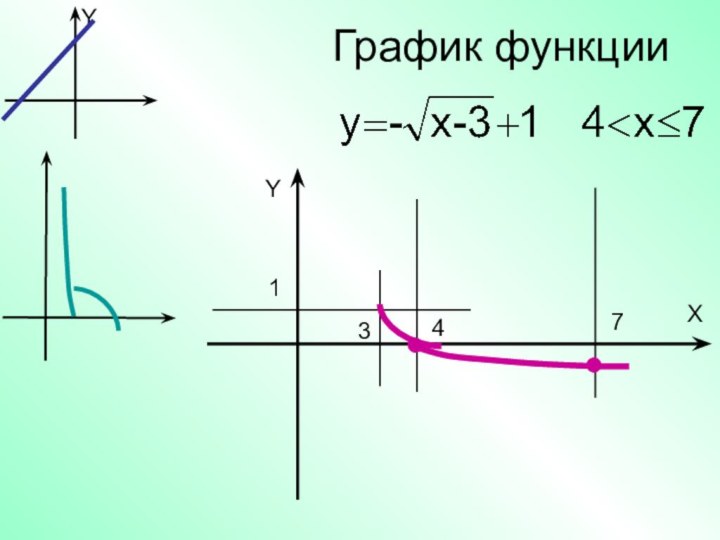
- 21. График функцииYX1347Y
- 22. Сбор графика-551247YX4
- 23. -551247X263Свойства графика кусочной функцииY-∞-∞D(f)ε(f)Y=0Y>0Y
- 24. Мастерская Масько Л.Г.Физминутка (коррекция зрения)
- 33. В классе:
- 34. Домашнее задание: Домашнее задание: Сборникна «5» -
- 35. Оценка за урок5 - 7
- 36. Скачать презентацию
- 37. Похожие презентации
"Числа не Боги, они не управляют миром, они показывают, как управляется мир" (поэт, гений немецкой литературы, Гёте)
Слайд 3
Эпиграфом нашего урока являются слова А. Эйнштейна:
“Весь
наш предшествующий опыт приводит к убеждению, что природа является осуществлением
того, что математически проще всего представить”.
Слайд 4
Цели урока:
1. Обобщить и систематизировать
материал по данной теме.
2. Продолжать развивать:
наблюдать, рассуждать, анализировать, делать выводы.
3. Провести диагностику усвоения системы знаний и ее применения для выполнения практических заданий стандартного уровня / самостоятельная работа по тестам ГИА /.
Слайд 5
Разминка
ч
е
т
н
а
я
н
е
ч
е
т
н
а
я
а
л
г
е
б
р
а
ф
у
н
к
ц
и
я
с
п
ь
Функция, график которой симметричен относительно оси Оу.
Функция, график,
которой симметричен относительно начала координат.
Предмет, изучаемый в школе.
Зависимость переменной
у от переменной х, при которой каждому значению х соответствует единственное значение переменной у.
Слайд 6
Свойства функций
(исследование функции)
Область определения функции;
Промежутки монотонности;
Ограниченность функции;
Наибольшее, наименьшее
значения функции;
Непрерывность функции;
Выпуклость функции;
Область значения функции.
Слайд 7
Функция задана графиком.
Укажите область определения
этой функции.
1
2 3 4 5 6
7-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
[-2; 4]
[-5; 5)
[-5; 5]
(-2; 4]
2
1
3
4
ПОДУМАЙ!
ВЕРНО!
Это множество значений!
ПОДУМАЙ!
Слайд 8
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком.
Укажите область определения
этой функции.
[-3; 5]
[-3; 5)
[-2; 5]
(-2; 5]
2
ВЕРНО!
1
3
4
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 9
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком.
Укажите множество значений
этой функции.
[-5; 7]
(-5; 7)
[-3; 5]
(-3; 5)
3
ВЕРНО!
1
2
4
Это область определения!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 10
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком.
Укажите область значений
этой функции.
[1; 6]
[-6; 5)
[-2; 6]
(-2; 6]
4
ВЕРНО!
1
3
2
Подумай!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 11
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком на [-4;0) (0;3].
Укажите множество значений
этой функции.
[1; 3]
[0; + )
[1; + ]
(-2; 4]
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 12
1 2 3 4 5
6 7
-7 -6 -5 -4 -3 -2
-17
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
Функция задана графиком.
Укажите наибольшее значение функции
5
4
3
-4
2
ВЕРНО!
1
3
4
ПОДУМАЙ!
ПОДУМАЙ!
ПОДУМАЙ!
Слайд 13
Укажите график четной функции.
4
2
3
1
ПОДУМАЙ!
ПОДУМАЙ!
Верно!
График симметричен относительно оси
Оу
ПОДУМАЙ!
Слайд 14
Укажите график нечетной функции.
3
4
3
1
ПОДУМАЙ!
Это четная функция!
ПОДУМАЙ!
Верно!
График симметричен
относительно точки О
Слайд 15 -4 -3 -2
-1
1 2 3 4 5
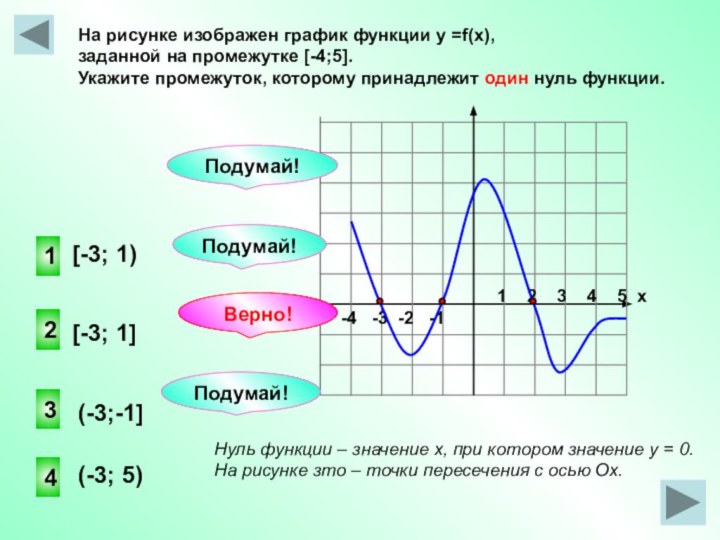
хНа рисунке изображен график функции у =f(x),
заданной на промежутке [-4;5].
Укажите промежуток, которому принадлежит один нуль функции.
3
2
4
1
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
[-3; 1)
[-3; 1]
(-3;-1]
(-3; 5)
Слайд 16 -4 -3 -2
-1
1 2 3 4 5
хНа рисунке изображен график функции у =f(x),
заданной на промежутке [-4;5].
Укажите промежуток, которому принадлежат все нули функции.
1
2
4
3
Подумай!
Подумай!
Верно!
Подумай!
Нуль функции – значение х, при котором значение у = 0. На рисунке зто – точки пересечения с осью Ох.
(1; 4]
(-3; 5)
(-3;4]
[-3;4]
Слайд 33
В классе:
Вариант - 1
Вариант - 2на «5» 5.29 (а) 5.29 (б)
на «4» 5.20 (а) 5.20 (б)
на «3» 5.18 (а) 5.18 (б)
Дополнительно
на «5» 4.25 (а) 4.25 (б)
на «4» 4.24 (а) 4.24 (б)
на «3» 4.10 (а) 4.10 (б)
Слайд 34
Домашнее задание:
Домашнее задание:
Сборник
на «5» - «4»
4.25 -4.24
на «3»
4.10Учебник
на «5» - «4» 13.14, 1 4.27
на «3» 13.9
