Слайд 2
СБЛИЖЕНИЕ ТЕОРИИ С ПРАКТИКОЙ ДАЕТ САМЫЕ БЛАГОТВОРИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ,
И НЕ ОДНА ТОЛЬКО ПРАКТИКА ОТ ЭТОГО ВЫИГРЫВАЕТ, САМИ
РУКИ РАЗВИВАЮТСЯ ПОД ВЛИЯНИЕМ ЕЕ.
Л.Л. ЧЕБЫШЕВ
Слайд 3
План:
Актуальность темы
Цель
Задачи
Геометрические методы в решении прикладных задач.
-Примеры кодирования Графической информации
-Примеры решения задач
Аналитические методы в решении прикладных задач.
-Способы задания функции
1.Табличный
2.Графический
3.Аналитический
4.Программный метод моделирования
-Примеры применения аналитических методов из судебной баллистики
1.Определение дистанции выстрела по следам металлизации на преграде. Исследование баллистической теории
2.Определение скорости полета пули
3. Определение дальности полета пули путем исследования баллистической кривой
-Решение прикладных задач
с использованием аналитического аппарата
Заключение
Слайд 4
Актуальность темы:
В условиях трансформационной
экономики России экономическая , правовая и социально-психологическая адаптация обучающихся
к условиям взрослой жизни становится объективной необходимостью. Мотивирующим потенциалом данной темы является формирование познавательного интереса к математике, связанной с правовой деятельностью. Ответ на этот вопрос мы попытались найти при разработке данного проекта. В процессе работы возникло много вопросов, при решении которых пришлось расширить область исследования. Изначально мы хотели выяснить только принципы работы экспертов-криминалистов, но кроме этого, пришлось собрать информацию о теории прикладной геометрии, разобрать решения задач и прорешать задачи, обусловленные жизненными ситуациями.
Слайд 5
Цель работы:
Применить геометрические методы при решении прикладных задач;
Иметь
представление об области применения математических методов;
Владеть практическими навыками применения
математических методов при решении конкретных задач.
Слайд 6
Задачи:
усвоение определенной системы знаний посредством моделирования и исследования
реальных ситуаций;
развитие ситуационного, аналитического, логического, рефлексивного мышления;
формирование творческого мышления
и способности отстаивать свое мнение;
создание условий личностного роста и профессионального определения.
Рис.1в
§1. Геометрические методы
в решении прикладных задач.
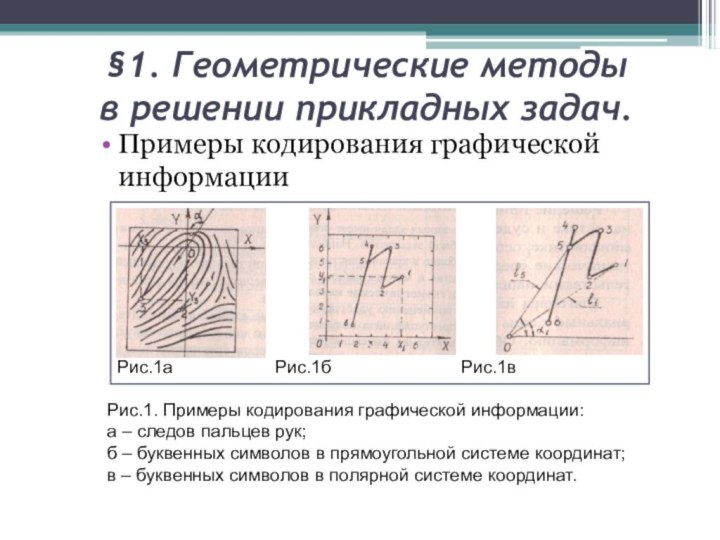
Примеры кодирования графической информации
Рис.1. Примеры кодирования графической информации:
а – следов пальцев рук;
б – буквенных символов в прямоугольной системе координат;
в – буквенных символов в полярной системе координат.
Слайд 8
Если нужно закодировать какой-нибудь графический объект, например, букву
«Р», ее изображение помещают в первую четверть прямоугольной системы
координат и условно делят на элементарные части (точки или отрезки). Координаты этих элементов служат тождественной кодовой информацией о конфигурации данного письменного знака (объекта).
Пример кодирования графической информации
.
Слайд 9
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ.
Решение:
В данном случае
величина малой оси эллипса примерно равна калибру ствола огнестрельного
оружия или диаметру пули.
Из рисунка видно, что величина большой оси D соответствует длине гипотенузы АС прямоугольного треугольника АВС, а величина малой оси d эллипса соответствует величине катета АВ. Отсюда необходимо найти угол α, который определяется как отношение противолежащего катета к гипотенузе:
АС·sinα=АВ отсюда sinα=AB/AC=d/D.
Величина синуса угла определяется по справочным таблицам.
Пример 1. При выстреле из огнестрельного оружия под углом α к преграде 1 пулевая пробоина имеет форму эллипса 2 (рис). определить угол выстрела α по отношению к преграде по форме пулевого отверстия и известных величинах большой D и малой d оси эллипса.
Слайд 10
Решение:
Угол α= углу β (вертикальные)
В
треугольнике АВО известен угол α = 30° и сторона
АВ (из условия задачи).
sinα=АО/АВ→АО=АВsinα
AO=27,5·0,5=13,75 мм.
Пример 2. Гражданину N был нанесен смертельный удар в область сердца. Специалисту необходимо предварительно установить вид холодного оружия, которым было совершено преступление. Для этого измеряют глубину раневого канала на теле, а также угол, под которым был нанесен удар. Необходимо определить ширину клинка холодного оружия по повреждению с целью установления вида холодного оружия. Длина повреждения (пореза) АВ – 27,5 мм, угол, под которым клинок вошел в преграду α = 30° (рис).
Слайд 11
Пример 3. С крыши дома №
23 по ул.Космонавтов, был произведен выстрел. Пуля попала в
соседнее здание, разбив стекло 2-го этажа. Перед специалистом стоит задача: рассчитать дистанцию выстрела АВ и высоту АД, с которой был произведен выстрел. При этом известно, что расстояние между зданиями 300 м, расстояние между пробоиной в стекле и полом NM=1,4м, МВ=2,56м.
Решение: рассмотрим подобные треугольники . составим пропорцию. AD:NM=DB:MB, отсюда следует AD=1,4·302,56:2,56=165,46м. Дистанцию выстрела АВ найдем с помощью теоремы Пифагора. АВ²=164,46²+302,56². Вычислим и получим 344,8 м
Слайд 12
Пример 4: При осмотре пулевой пробоины
было установлено что выстрел был произведен под углом α
к преграде. Измерения геометрических параметров показали, что большая диагональ пробоины составляет D=14мм, а меньшая диагональ d=9мм. Определите калибр оружия и угол, под которым был произведен выстрел.
Решение: калибр равен величине меньшей диагонали эллипса , то есть 9 мм. Угол найдем с помощью тригонометрической функции sinα=AB/AC=d/D и таблиц Брадиса. Ответ 40°.
Слайд 13
§2. Аналитические методы
в решении прикладных задач.
Объектом изучения математического
анализа являются только переменные величины, изменяющие свои величины с
течением времени. Переменные величины можно разделить на две основные группы:
Независимые (аргумент) – изменяющиеся произвольным образом;
Зависимые (функция) – изменяются при изменении независимых переменных.
Слайд 14
Способы задания функции.
1.Табличный.
Преимущества:
Простота нахождения значений функций по значению аргумента без
дополнительных измерений и вычислений.
Недостатки:
Не позволяет находить промежуточные значения одной переменной (зависимой) по заданному значению аргумента;
Не позволяет наглядно предоставить картину изменения значений функции в зависимости от значений аргумента, т.е. закон изменения функции;
Таблица не может содержать всех значений аргумента, при которых данная функция определена, поскольку с уменьшением интервала значений аргумента таблица становится громоздкой.
Слайд 15
График зависимости
температуры кипения воды от величины атмосферного давления.
2.Графический.
Графиком функции в декартовой прямоугольной
системе координат называют геометрическое место точек, абсциссы которых являются значениями независимой переменной, а ординаты – соответствующими значениями функции. Графический способ задания функции имеет неоспоримое преимущество перед остальными способами задания функции – наглядность
Слайд 16
3.Аналитический.
Преимущества:
Возможно определить значения функции
для любого значения аргумента;
Возможно применить аппарат
математического анализа для исследования функциональных зависимостей.
Недостатки:
Недостаточная наглядность и возможною трудоемкость вычислений.
Слайд 17
4.Программный метод моделирования.
При условии применения программного
метода функция задается с помощью перфокарт, перфолент или магнитных
носителей. Данный метод широко применяется с вычислительной технике. Метод моделирования позволяет воспроизводить функцию при помощи специальных логических и электронных устройств. Реализация данного способа стала возможна с появлением компьютерной техники.
Слайд 18
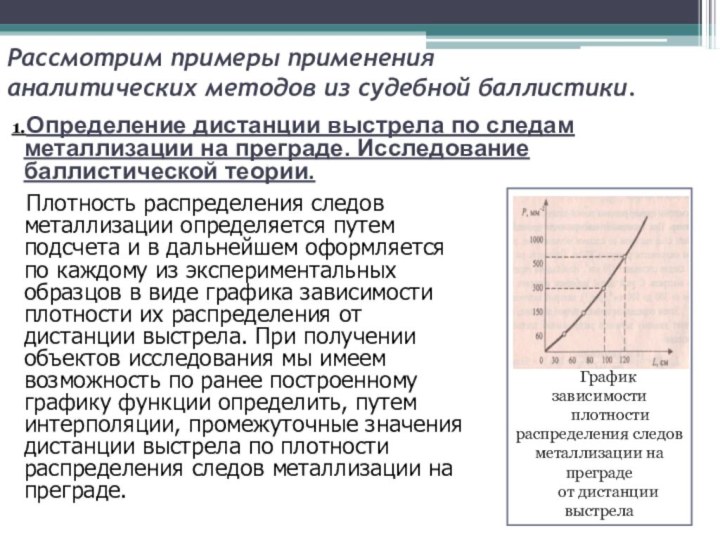
График зависимости
плотности распределения следов металлизации на преграде
от
дистанции выстрела
Рассмотрим примеры применения
аналитических методов из судебной
баллистики.
1.Определение дистанции выстрела по следам металлизации на преграде. Исследование баллистической теории.
Плотность распределения следов металлизации определяется путем подсчета и в дальнейшем оформляется по каждому из экспериментальных образцов в виде графика зависимости плотности их распределения от дистанции выстрела. При получении объектов исследования мы имеем возможность по ранее построенному графику функции определить, путем интерполяции, промежуточные значения дистанции выстрела по плотности распределения следов металлизации на преграде.
Слайд 19
2.Определение скорости полета пули.
Метод баллистического маятника.
Этот
метод основан на физическом законе сохранения суммарного импульса системы
тел при их соударении. Баллистический маятник представляет собой массивное тело, укрепленное на подвесе (рис).
.
Слайд 20
Схема определения скорости полета пули
с помощью механического хронографа
Механический хронограф.
Одна из конструкций механического хронографа представляет собой два
вращающихся бумажных диска, закрепленных на одной вращающейся оси. При выстреле пуля пробивает сначала один, а затем второй диск.
Время движения пули между дисками определяется по величине угла поворота дисков от пробоины до пробоины (рис).
Слайд 21
3. Определение дальности полета пули путем
исследования баллистической кривой.
Известно, что траектория полета снаряда соответствует кривой,
близкой к параболе. Практически эксперт сталкивается с решением подобной задачи при определении дальности полета пули и установлении возможности поражения цели с предполагаемого места выстрела. Чаще всего приходится сталкиваться с восходящей траекторией полета снаряда, т.е. ее восходящей ветвью.
Слайд 22
Решение прикладных задач
с использованием аналитического аппарата.
Пример. При проведении
баллистической экспертизы гладкоствольного оружия эксперт определяет дистанцию выстрела по
повреждениям на преграде. В ходе экспертного определения из данного экземпляра оружия производится серия выстрелов по отдельным мишеням, расположенным на разном расстоянии L от дульного среза ствола. С увеличением дистанции выстрела разброс дроби будет увеличиваться, соответственно, размеры осыпей дроби для фиксированных расстояний L.
Затем для каждой дистанции определяют максимальный и минимальный размеры повреждения, соответствующие большой и малой оси эллипса. Построив графики зависимостей максимального (L) и минимального (L), по известному диаметру осыпи дроби с места происшествия Dn определяют максимально и минимально возможные дистанции выстрела.
Определить расстояние по диаметру Dn=45см.