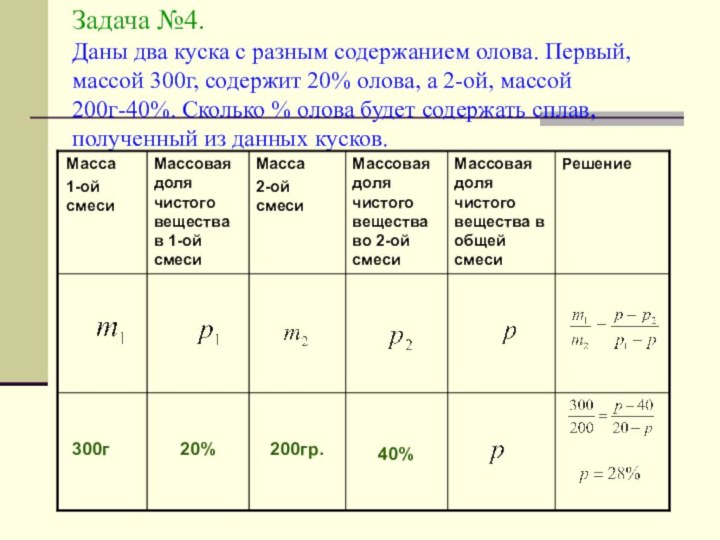
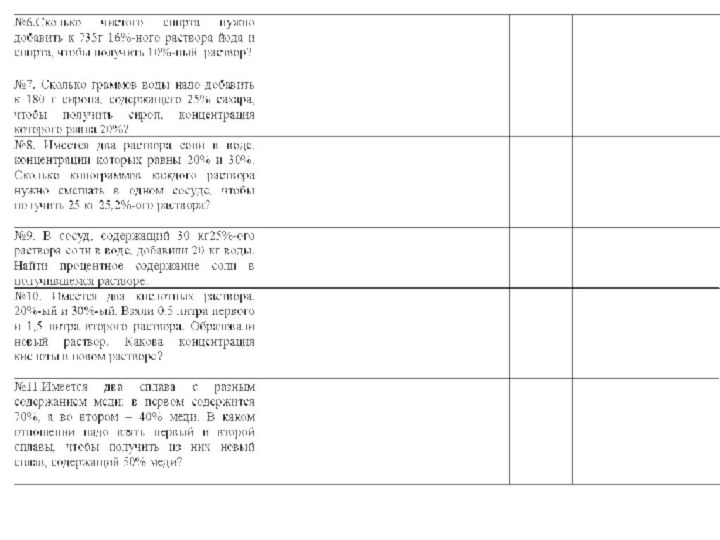
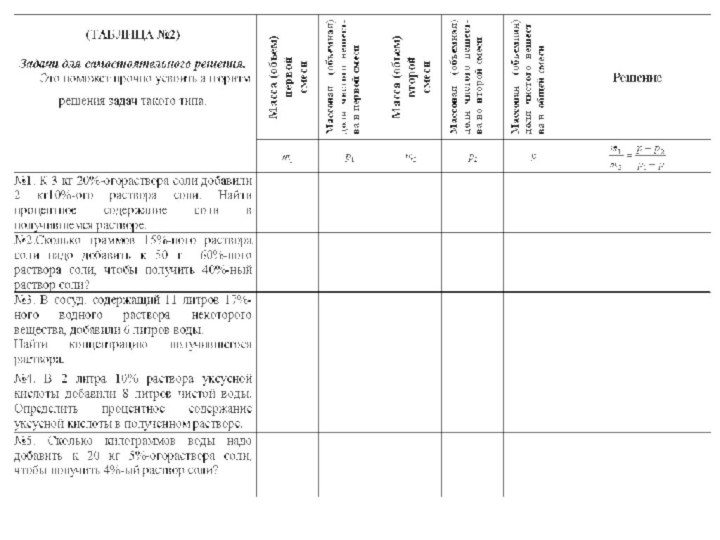
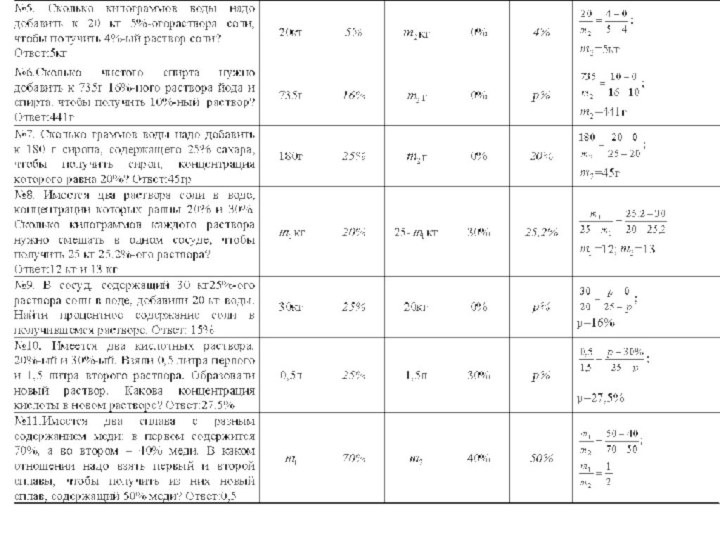
«на смеси, сплавы, растворы»
Перед тем, как приступить к решению подобных задач, примем некоторые допущения.
Все получающиеся сплавы или смеси однородны. При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
Определение. Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси.
Это отношение может быть выражено либо в дробях, либо в процентах. Терминология:
процентное содержание вещества;
концентрация вещества;
массовая доля вещества.
Все это синонимы.
В данной работе чаще упоминается термин «массовая доля», .
Концентрация – это безразмерная величина. Сумма массовых долей всех компонент, составляющих смесь, очевидно, равна единице.