Слайд 2
Данная тема представляет особую актуальность, так как в
школьной программе по геометрии эта тема практически не рассматривается,
но при решении некоторых видов задач часто встречается.
Объект исследования:
Пифагоровы и героновы тройки.
Предмет исследования: числа
Слайд 3
Цель работы– обосновать теоретическую и практическую значимость пифагоровых
и героновых троек в области математики и в жизнедеятельности
человека.
Задачи:
1)Установить способы получения пифагоровых и героновых чисел.
2)Изучить свойства примитивных пифагоровых и героновых троек, составить их таблицу.
3)Предложить решения некоторых задач с помощью пифагоровых и героновых троек.
4)Выявить практическое применение пифагоровых и героновых троек.
Слайд 4
Пифагоровы числа – тройки натуральных чисел, таких, что
треугольник, длины которого пропорциональны (или равны) этим числам, является
прямоугольным. По теореме, обратной теореме Пифагора, для этого достаточно, чтобы они удовлетворяли диофантову уравнению x2 + y2 = z2 .
Таковы, например, числа х=3, у=4,z=5.
—
Пифагор Самосский
Слайд 5
В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный
из двух прямоугольных со сторонами 9, 12 и 15
локтей.
Слайд 6
Пирамиды Фараона Снофру (27 век до н. э.)
построены с использованием треугольников со сторонами 20, 21 и
29, а также 18, 24 и 30 десятков египетских локтей.
Слайд 7
Способы нахождения пифагоровых троек
Способ первый: Запишем подряд квадраты

натуральных чисел, отделив их друг от друга запятой. Под
каждой запятой подпишем разность между последовательными квадратами:
1 , 4 , 9 , 16 , 25 , 36 , 49 , 64 , 81 , 100 , 121 , 144 , 169 , 196 ,...
3 , 5 , 7 , 9 , 11 , 13 , 15 , 17 , 19 , 21 , 23 , 25 , 27 ,..
А теперь внимание! В нижней строке есть квадратные числа! Первое из них 9 = 3², над ними 16 = 4² и 25 = 5² - знакомая нам пифагорова тройка (3, 4, 5).
Следующее квадратное число в нижней строке 25, ему соответствуют 144 и 169, отсюда находим вторую известную нам тройку 5, 12, 13. Если продолжить строку квадратных чисел и посчитать соответствующие разности, то во второй строке найдете 49 = 7² , этому числу отвечают в строке квадратов 576 = 24² и 625 = 25² . И действительно, 7² + 24² = 25² . Это уже третья тройка. Она была известна еще в Древнем Египте. Но, составлять такие последовательности довольно скучное и трудоемкое занятие. По формуле находить такие тройки и проще и быстрее.
Слайд 8
Способ второй: Эти формулы были известны уже две
с половиной тысячи лет назад. Пусть (x, y, z,)
– пифагорова тройка и x –нечетное число. Тогда y = (x²-1)/2 и z =(x²+1)/2. По этому правилу можно получить уже известные нам тройки:
Если x = 3, то y =(3²-1)/2=4 , z = 3²+1/2=5, получилась первая тройка (3, 4, 5).
Если x = 5, то y = (5²-1)/2 =12, z = (5²+1)/2=13, вторая тройка (5, 12, 13).
Если x = 7, то y = (7²-1)/2=24 , z = (7²+1)/2=25, третья тройка (7, 24, 25) и так далее.
Слайд 9
Способ третий: Теперь установим правила вычисления всех, а
не только некоторых пифагоровых троек. Перепишем уравнение Пифагора следующим
образом: х² = z²– ² или х² = (z – y)(z + y)
Это значит, что число x² должно раскладываться на два неравных множителя (z + y) и (z–y), которые мы обозначим так, что получится система:
z + y = 2m²,
z – y = 2n²
х² = z²– ² или х² = (z – y)(z + y)
Решив эту систему, получим:
z = m² + n², y = m² – n², тогда подставляя в равенство для х², получаем, что x = 2mn, где m и n – произвольно взятые взаимно простые натуральные числа, причем m>n. Применяя указанные формулы, легко найти все решения уравнения x2 + y2 = z2 в натуральных числах. Например: пусть m = 9, n = 7 , где m>n.
Решим уравнение по формулам:
x = 2mn, x = 2* 9 *7 = 126;
y = m² – n², y = 81 – 49 = 32;
z = m² + n², z = 81 + 49 = 130.
Действительно, 126 + 32 = 130, так как 15876 + 1024 = 16900
Ответ: 126, 32, 130.
Слайд 10
Свойства пифагоровых троек
Рассмотрим некоторые свойства пифагоровых троек.
Свойство 1. Числа,
входящие в простейшую пифагорову тройку, попарно взаимно просты.
Действительно, если
два из них, например x и y имеют простой общий делитель p, то из равенства x2 + y2 = z2 следует, что на p делится и третье число z. Это противоречит тому, что тройка - простейшая.
Следствие. В простейшей пифагоровой тройке только одно число может быть чётным.
Свойство 2. В простейшей пифагоровой тройке числа x и y не могут быть одновременно нечётными.
Пифагор нашёл формулы, которые в современной символике могут быть записаны так: a=2n+1, b=2n (n+1), c=2 n2 +2n+1, где n - целое число.
Эти числа - пифагоровы тройки. Пифагоровы числа обладают рядом любопытных особенностей:
· Один из катетов должен быть кратен трём.
· Один из катетов должен быть кратен четырём.
· Одно из пифагоровых чисел должно быть кратно пяти.
Слайд 11
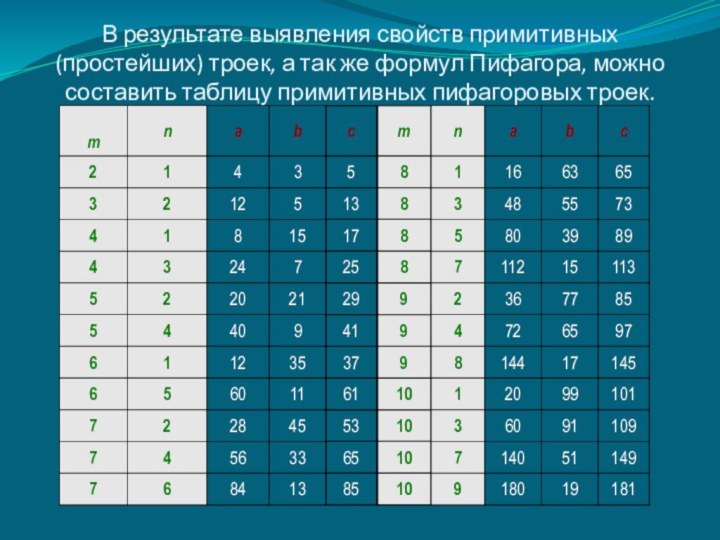
В результате выявления свойств примитивных (простейших) троек, а
так же формул Пифагора, можно составить таблицу примитивных пифагоровых
троек.
Слайд 12
Героновы числа
В тесной связи с пифагоровыми числами
находятся героновы числа. Последние получили свое название по имени
Герона Александрийского, который дал миру формулу для вычисления площади треугольника по его сторонам.
Героновой тройкой чисел называют три натуральных числа, выражающих длины сторон треугольника, площадь которого тоже есть натуральное число.
ГЕРОН АЛЕКСАНДРИЙСКИЙ
Слайд 13
Способы нахождения героновых троек
Чтобы найти все возможные героновы
тройки, мы прежде всего примем, что треугольник имеет три
рациональные стороны а, b, с и площадь S, которая выражается рациональным числом. В таком случае и все высоты h должны выражаться рациональными числами. Для получения всевозможных треугольников с рациональными сторонами и рациональной площадью достаточно сложить всеми возможными способами два прямоугольных треугольника с рациональными сторонами. Три стороны всякого треугольника после соответствующего умножения дают геронову тройку.
Слайд 14
Из пифагоровых-героновы
Особым видом героновых троек являются
такие, в которых два числа равны. Такие тройки получаются
сопоставлением чисел пифагоровой тройки с самими этими числами. Из каждой пифагоровой тройки таким образом получаем героновы тройки. Например, пифагоровы числа 5, 3, 4 дают героновы тройки 5, 5, 6 и 5, 5, 8;
Числа 13, 5, 12 -13, 13, 10 и 13, 13, 24.
Числа 17. 15, 8 – 17, 17, 30 и 17, 17, 16.
Слайд 15
. Практическое применение пифагоровых и героновых троек
Пифагоровы и
героновы тройки имеют огромное практическое применение. Рассмотрим для примера
несколько задач:
Задача №1. Найти cos , tg и ctg , если sin = 24/25, если – угол второй четверти.
Решение:Исходя из определения cos, tg и ctg острого угла прямоугольного треугольника, учитывая, что числа 7 и 24 – это катеты, а 25 – гипотенуза и, зная, в какой четверти ннаходится угол, записываем: cos = - 7/25, tg = - 24/7, ctg = - 7/24.
Слайд 16
Задача №2. При оформлении фасада дома мозаикой, требуются
разноцветные равные прямоугольные треугольники из стекла, с целочисленными сторонами
и с катетом 10 см. Требуется определить, какими должны быть другие стороны данных треугольников.
Решение: Заданный катет – четное число, значит х = 10 = 2mn, где m>n и они взаимно простые числа. Возможна единственная комбинация m и n – это 5 и 1. Так как 2*5*1=10. Остальные стороны равняются у=m²-n²=24, z=m²+n²=26. Таким образом, ответ – это треугольники со сторонами 10см, 24 см и 26 см.
Слайд 17
ЗАКЛЮЧЕНИЕ
Изначально были выявлены базовые
теоретические знания, включающие описание общих понятий о пифагоровых и
героновых тройках. На базе полученных знаний были выявлены способы их получения и свойства. Теоретическая и практическая значимость исследования состоит в том, что в нем на основе системного подхода представлена роль, которую играет открытие пифагоровых и героновых троек в науке и в жизнедеятельности человека. Несмотря на то, что в школе изучение пифагоровых и героновых троек не отводится много времени, в настоящее время значение их необходимо при решении многих задач. А умы учёных продолжают искать новые варианты доказательств теоремы Пифагора.