Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему по алгебре на тему Уравнение прямой вида у = kх + l

Содержание

2. 33. 03. 18Классная работаУравнение прямой вида у = kх + l
3. Вам уже неоднократно приходилось решать линейное уравнение
4. В таком виде можно представить любое линейное
5. Запись уравнения прямой в виде у =
6. Положение в координатной плоскости прямой, заданной уравнением
7. Чтобы выяснить, в чём состоит эта зависимость,
8. у = kхВ самом деле, если х
9. Построим в одной и той же системе
10. Прямая у = 2х, проходя через третий
11. Прямая у = -1/3х, проходя через
12. И вообще,если k > 0, то угол,
13. На рисунке 4.17, а, б построены графики
14. Работа с учебником№ 607(а, в); № 608(а,
15. Домашнее задание№ 607(б, г); № 608(б, г);
16. Урок 2Алгебра 8 класс
18. Выясним теперь, каково взаимное расположение прямых, заданных
19. Построим в одной системе координат две такие
20. Точно так же каждая из прямых у
21. Из этих рассуждений понятно, что величина угла
22. Если у двух несовпадающих прямых угловые коэффициенты одинаковы, то эти прямые параллельны.
23. Если же две прямые имеют разные угловые
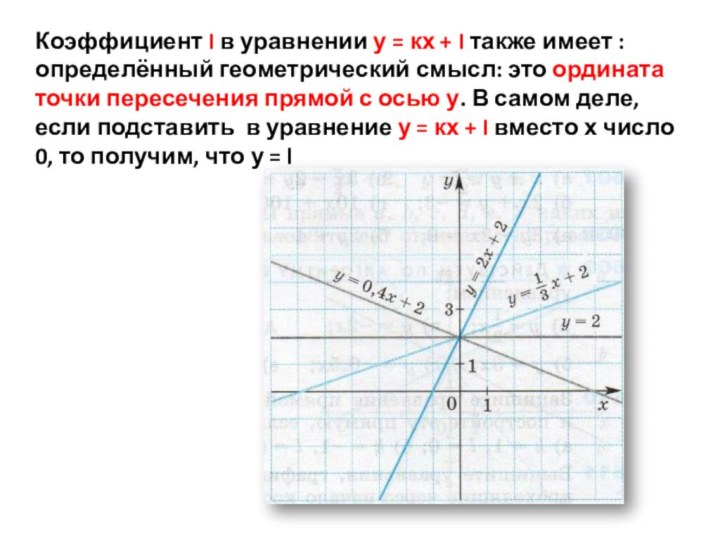
24. Коэффициент I в уравнении у = кх
25. На рисунке 4.20 построено несколько прямых, каждая
26. Скачать презентацию
27. Похожие презентации

33. 03. 18Классная работаУравнение прямой вида у = kх + l

Главная
Алгебра
Презентация по алгебре на тему Уравнение прямой вида у = kх + l

33. 03. 18Классная работаУравнение прямой вида у = kх + l

Вам уже неоднократно приходилось решать линейное уравнение с двумя переменными относительно переменной

В таком виде можно представить любое линейное уравнение вида ах + bу

Запись уравнения прямой в виде у = kх + Ɩ очень удобна.

Положение в координатной плоскости прямой, заданной уравнением вида

Чтобы выяснить, в чём состоит эта зависимость, остановимся сначала на частном случае,

Построим в одной и той же системе координат прямые, заданные уравнениями у

Прямая у = 2х, проходя через третий и первый координатные углы, поднимается

Прямая у = -1/3х, проходя через второй и четвёртый координатные углы,

И вообще,если k > 0, то угол, который образует луч, являющийся частью

На рисунке 4.17, а, б построены графики уравнений у = kх при

Работа с учебником№ 607(а, в); № 608(а, в);

Домашнее задание№ 607(б, г); № 608(б, г);

Презентация по алгебре на тему Уравнение прямой вида у = kх + l

Выясним теперь, каково взаимное расположение прямых, заданных уравнениями вида у = kх

Построим в одной системе координат две такие прямые, например прямые

Точно так же каждая из прямых у = 0,5х - 1, у

Из этих рассуждений понятно, что величина угла между лучом Ох и частью

Если у двух несовпадающих прямых угловые коэффициенты одинаковы, то эти прямые параллельны.

Если же две прямые имеют разные угловые коэффициенты, то эти прямые пересекаются.

Коэффициент I в уравнении у = кх + I также имеет :

На рисунке 4.20 построено несколько прямых, каждая из которых задаётся уравнением вида

Слайды презентации

Слайд 2 33. 03. 18
Классная работа
Уравнение прямой вида
у =

kх + l

Слайд 3 Вам уже неоднократно приходилось решать линейное уравнение с

Вам уже неоднократно приходилось решать линейное уравнение с двумя переменными относительно

двумя переменными относительно переменной у.
При этом получается уравнение

вида у = kх + Ɩ , где k и Ɩ — некоторые числа.

Например, решив относительно у уравнение Зх - 2у = 6, получаем уравнение у = 1,5х - 3, где k = 1,5 и Ɩ = -3.

Слайд 4 В таком виде можно представить любое линейное уравнение

В таком виде можно представить любое линейное уравнение вида ах +

вида ах + bу = с,

у которого коэффициент при у отличен от 0. Иными словами, в таком виде может быть записано уравнение любой прямой, кроме вертикальной.

Слайд 5 Запись уравнения прямой в виде у = kх

Запись уравнения прямой в виде у = kх + Ɩ очень

+ Ɩ очень удобна.
Не выполняя построения этой

прямой , легко узнать, как она расположена в координатной плоскости.

Слайд 6 Положение в координатной плоскости прямой, заданной уравнением вида

у = kх + Ɩ, зависит от значений коэффициентов k и Ɩ.

Слайд 7 Чтобы выяснить, в чём состоит эта зависимость, остановимся

Чтобы выяснить, в чём состоит эта зависимость, остановимся сначала на частном

сначала на частном случае, когда Ɩ = 0, т.

е. рассмотрим график уравнения у = kх.

Прежде всего отметим следующий факт:
Прямая, которая является графиком уравнения у = kх, проходит через начало координат.

Слайд 8 у = kх
В самом деле, если х =

0, то и у = 0, а это и

означает, что точка 0(0; 0) принадлежит графику.
Обратите внимание: для построения прямой у = kх достаточно найти координаты одной лишь её точки: вторая уже имеется — это начало координат.

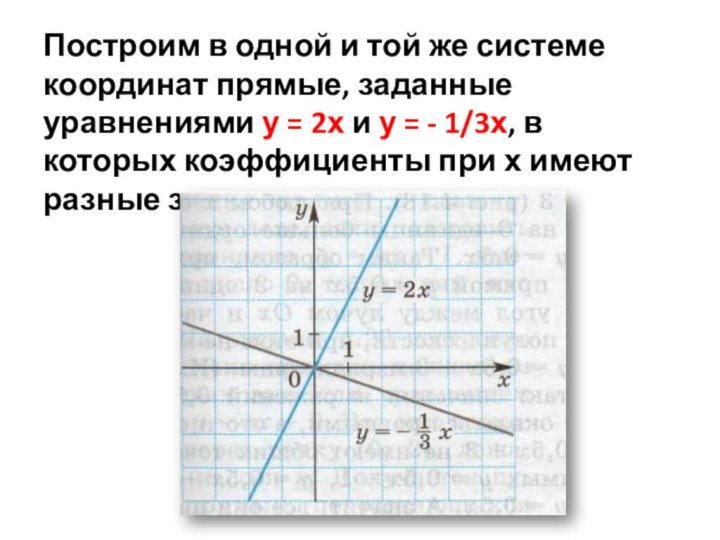
Слайд 9 Построим в одной и той же системе координат

Построим в одной и той же системе координат прямые, заданные уравнениями

прямые, заданные уравнениями у = 2х и у =

- 1/3х, в которых коэффициенты при х имеют разные знаки.

Слайд 10 Прямая у = 2х, проходя через третий и

Прямая у = 2х, проходя через третий и первый координатные углы,

первый координатные углы, поднимается вверх; так выглядит график любого

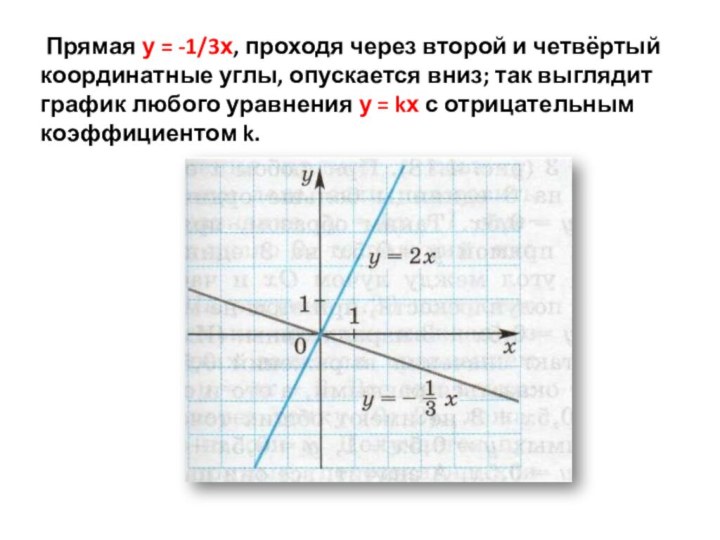
уравнения у = kх с положительным коэффициентом k.

Слайд 11 Прямая у = -1/3х, проходя через второй

Прямая у = -1/3х, проходя через второй и четвёртый координатные

и четвёртый координатные углы, опускается вниз; так выглядит график

любого уравнения у = kх с отрицательным коэффициентом k.

Слайд 12 И вообще,
если k > 0, то угол, который

И вообще,если k > 0, то угол, который образует луч, являющийся

образует луч, являющийся частью прямой у = kх и

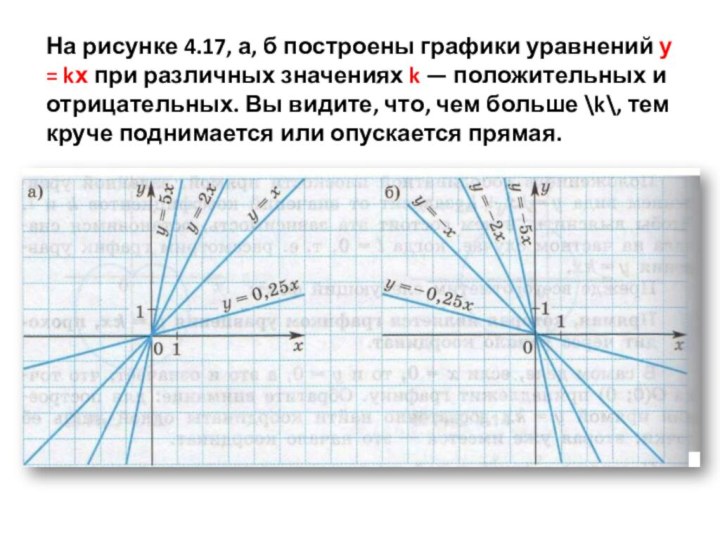
расположенный в верхней полуплоскости, с лучом Ох,— острый; если k < 0, то этот угол тупой . (Если k = 0, то график уравнения у = kх совпадает с осью X.)

Слайд 13 На рисунке 4.17, а, б построены графики уравнений

На рисунке 4.17, а, б построены графики уравнений у = kх

у = kх при различных значениях k — положительных

и отрицательных. Вы видите, что, чем больше \k\, тем круче поднимается или опускается прямая.

Слайд 14 Работа с учебником
№ 607(а, в); № 608(а, в);

№ 609(а, в, д); № 610 (а, в); № 613;
№ 614;

Слайд 15 Домашнее задание
№ 607(б, г); № 608(б, г);

№ 609(б, г, е); № 610 (б, г); № 612;
№ 614;

Слайд 16 Урок 2
Алгебра 8 класс

Слайд 17

Слайд 18 Выясним теперь, каково взаимное расположение прямых, заданных уравнениями

Выясним теперь, каково взаимное расположение прямых, заданных уравнениями вида у =

вида у = kх + I, в которых коэффициенты

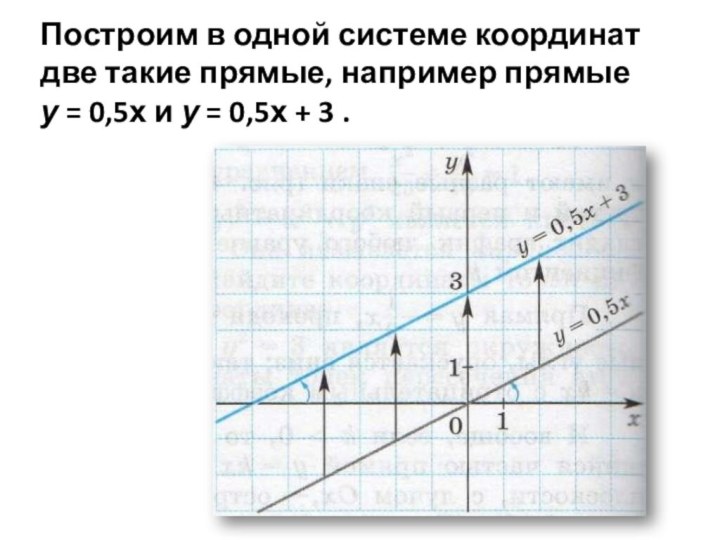
при х одинаковы.

Слайд 19 Построим в одной системе координат две такие прямые,

например прямые

у = 0,5х и у = 0,5х + 3 .

Слайд 20 Точно так же каждая из прямых у =

Точно так же каждая из прямых у = 0,5х - 1,

0,5х - 1, у = 0,5х + 2,5. у

= 0,5х - 4 параллельна прямой у = 0,5х. А значит, все они параллельны между собой .

Слайд 21 Из этих рассуждений понятно, что величина угла между

Из этих рассуждений понятно, что величина угла между лучом Ох и

лучом Ох и частью прямой

у = kx + I, расположенной в верхней полуплоскости, зависит только от значения коэффициента k. Поэтому k называют угловым коэффициентом прямой у = kх + I.