- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тангенс суммы и разности аргументов презентация для 10 класса
Содержание
- 2. ЦелиИзучить формулы тангенса суммы и разности аргументов.Рассмотреть практическое применение данных формул.
- 3. ПовторимСинус суммы двух аргументов равен произведению синуса
- 4. ПовторимКосинус суммы двух аргументов равен произведению косинусов этих аргументов минус произведение синусов этих аргументов.
- 5. ПовторимСинус разности двух аргументов равен произведению синуса
- 6. ПовторимКосинус разности двух аргументов равен произведению косинусов этих аргументов плюс произведение синусов этих аргументов.
- 7. Выведем формулу тангенса суммы двух аргументовПо определению
- 8. Разделим числитель и знаменатель последней дроби наПри всех допустимых значениях х и у
- 10. Получили:Аналогично можно доказать, что
- 11. Пример 1.Вычислить:Решение.
- 12. Пример 2.Вычислить:Решение.
- 13. Пример 3.Вычислить:Решение.
- 14. Историческая страничка
- 15. Замена хорд синусами стала главным достижением средневековой
- 16. Тригонометрия необходима для астрономических расчётов, которые оформляются
- 17. Южноиндийские математики в XVI веке добились больших
- 18. Так, ряды для синуса и косинуса вывел Исаак
- 19. Джеймс ГрегориДата рождения: 1638Место рождения: Драмоук, ШотландияГотфрид Вильгельм ЛейбницДата
- 20. Скачать презентацию
- 21. Похожие презентации
ЦелиИзучить формулы тангенса суммы и разности аргументов.Рассмотреть практическое применение данных формул.








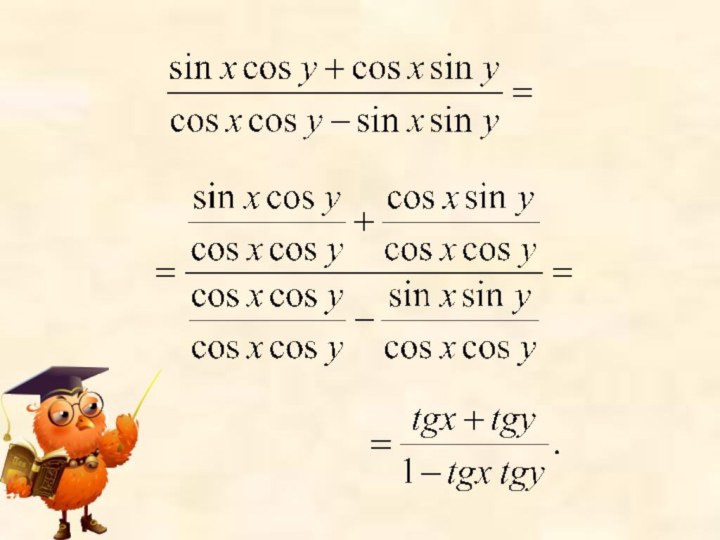











Слайд 2
Цели
Изучить формулы тангенса суммы и разности аргументов.
Рассмотреть практическое
применение данных формул.
Слайд 3
Повторим
Синус суммы двух аргументов равен произведению синуса первого
аргумента на косинус второго плюс произведение косинуса первого аргумента
на синус второго.
Слайд 4
Повторим
Косинус суммы двух аргументов равен произведению косинусов этих
аргументов минус произведение синусов этих аргументов.
Слайд 5
Повторим
Синус разности двух аргументов равен произведению синуса первого
аргумента на косинус второго минус произведение косинуса первого аргумента
на синус второго.
Слайд 6
Повторим
Косинус разности двух аргументов равен произведению косинусов этих
аргументов плюс произведение синусов этих аргументов.
Слайд 7
Выведем формулу тангенса суммы двух аргументов
По определению тангенс
есть отношение синуса к косинусу одного и того же
аргументаПо изученным формулам синуса и косинуса суммы, получим
Слайд 15 Замена хорд синусами стала главным достижением средневековой Индии.
Такая замена позволила вводить различные функции, связанные со сторонами
и углами прямоугольного треугольника. В Индии было положено начало тригонометрии как учению о тригонометрических величинах.Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как
Средневековая Индия
Слайд 16
Тригонометрия необходима для астрономических расчётов, которые оформляются в
виде таблиц. Первая таблица синусов имеется в «Сурья-сиддхантеТригонометрия необходима
для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у АриабхатыТригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.Статуя Ариабхаты. Индийский межуниверситетский центр астрономии и астрофизики (IUCAA)
Слайд 17 Южноиндийские математики в XVI веке добились больших успехов
в области суммирования бесконечных числовых рядов. В анонимном трактате
«Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв.Слайд 18 Так, ряды для синуса и косинуса вывел Исаак НьютонТак,
ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а
ряд арктангенса был найден Дж. ГрегориТак, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.Исаак Ньютон