Слайд 2
«Если вы хотите научиться плавать,
то смело входите
в воду,
а если хотите научиться решать задачи,
то
решайте их»
Д. Пойя
Слайд 3
При решении текстовых задач могут помочь несколько простых
и общих советов:
Прочитайте и тщательно изучите условие задачи.
Попытайтесь
полученную информацию представить в другом виде – это может быть рисунок, таблица или просто краткая запись условия задачи.
Выбор неизвестных.
Составление и решение «математической модели». (При составлении «математической модели» (уравнения, неравенства, системы уравнений или неравенств) еще раз внимательно прочитайте условие задачи. Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый «знак» полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).
Решить полученное уравнение, систему, неравенство. (Если решение задачи не получается, то нужно еще раз прочитать и проанализировать задачу.)
Слайд 4
Текстовые задачи ОГЭ можно разделить на три группы
I) задачи на движение;
II) задачи на производительность;
III) задачи на проценты, концентрацию, части, доли.
Основными типами задач на движение являются следующие:
1) задачи на движение по прямой (навстречу и вдогонку);
2) задачи на движение по замкнутой трассе;
3) задачи на движение по воде;
4) задачи на среднюю скорость;
5) задачи на движение протяжённых тел.
Слайд 5
Движение навстречу
Расстояние между городами А и В
равно 580 км. Из города А в город В
со скоростью 80 км/ч выехал автомобиль, а через два часа после этого навстречу ему из города В выехал со скоростью 60 км/ч второй автомобиль. Через сколько часов после выезда второго автомобиля автомобили встретятся?
Решение:
1) 80*2=160(км) – проехал первый автомобиль
2) (580-160)/(80+60)=3(ч)
Ответ: 3
Слайд 6
2. Движение вдогонку
Два пешехода отправляются из одного
и того же места в одном направлении на прогулку
по аллее парка. Скорость первого на 1 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 200 метрам?
Решение:
200м = 0,2 км.; ;
0, 2 часа=12 минут
Ответ: 12.
Слайд 7
3. Движение по окружности
(замкнутой трассе)
Из одной
точки круговой трассы, длина которой равна 10 км/ч, одновременно
в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 90 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Решение: Пусть скорость второго автомобиля х км/ч.
Т.к.40 мин. = часа и это время, за которое первый автомобиль будет опережать второй на один круг, составим уравнение
30 = 180 – 2х; 2х = 150; х = 75
Ответ: 75.
Слайд 8
4. Движение по воде
От лесоповала вниз по
течению реки движется со скоростью 3 км/ч плот. Плотовщик
доплывает на моторке из конца плота к его началу и обратно за 16 минут 40 секунд. Найдите длину плота, если собственная скорость моторки равна 15 км/ч. Ответ дайте в километрах.
Решение: Пусть длина плота х км. Тогда скорость моторки по течению 18 км/ч, а против течения 12 км/ч.
Т.к.16мин40с = часа, то
;
2х + 3х = 10;
5х = 10;
х = 2. Ответ: 2
Слайд 9
5. Средняя скорость
Путешественник переплыл море на
яхте со средней скоростью 20 км/ч. Обратно он летел
на спортивном самолёте со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
Решение:
25t=960; t = 38,4
Ответ: 38,4.
Слайд 10
6.Движение протяжённых тел.
Поезд, двигаясь равномерно со скоростью 65
км/ч, проезжает мимо идущего в том же направлении параллельно
путям со скоростью 5 км/ч пешехода за 30 секунд. Найдите длину поезда в метрах.
Решение: 65-5 =60 (км/ч)
60 км/ч=
Ответ: 500.
Слайд 11
При решении текстовых задач, с моей точки зрения,
удобнее использовать таблицу, которая нагляднее и короче обычной записи
с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.
Слайд 12
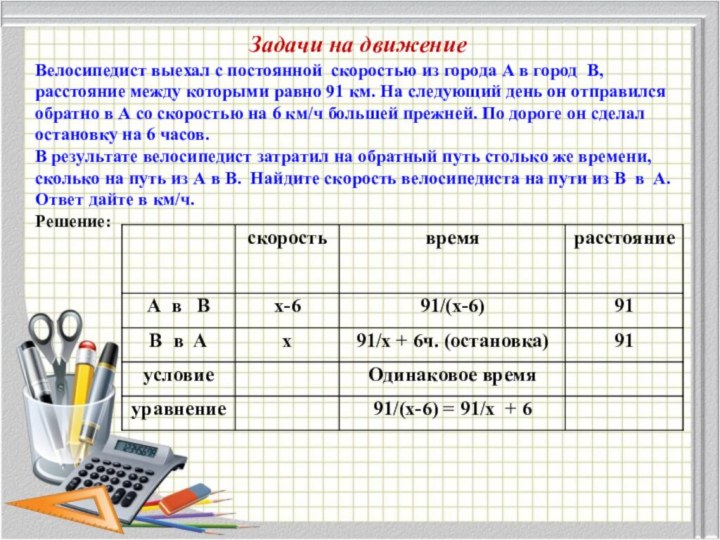
Задачи на движение
Велосипедист выехал с постоянной скоростью из
города А в город В, расстояние между которыми равно
91 км. На следующий день он отправился обратно в А со скоростью на 6 км/ч большей прежней. По дороге он сделал остановку на 6 часов.
В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч.
Решение:
Решение:
х≠0;х≠6 91х=91(х-6)+6х(х-6)
91х=91х-546+6 -36х
6 -36х-546=0|:6
-6х-91=0
, (не удовлетворяет условию задачи)
Ответ: 13км/ч.
Слайд 14
Из пункта А круговой трассы выехал велосипедист, а
через 30 минут следом за ним отправился мотоциклист. Через
10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Решение: 10 мин=1/6ч, 40мин=2/3ч, 30 мин=1/2 ч
Пусть х км/ч – скорость велосипедиста, у км/ч- скорость мотоциклиста.
Оба проехали одинаковое расстояние, т.е. (2/3)х =(1/6)у
Слайд 15
Из пункта А круговой трассы выехал велосипедист, а
через 30 минут следом за ним отправился мотоциклист. Через
10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Затем мотоциклист второй раз обогнал велосипедиста.
Мотоциклист обогнал велосипедиста. Значит, он проехал на 1
круг больше. Один круг – это длина трассы, она равна 30 км.
Получим уравнение: (1/2)у-(1/2)х=30.
Остается решить систему уравнений:
20 км/ч – скорость велосипедиста
20·4=80 км/ч- скорость мотоциклиста
Ответ: 80 км/ч.
Слайд 16
Задачи на работу
Два оператора, работая вместе, могут набрать
текст газеты объявлений за 8 ч. Если первый оператор
будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно? 75%=3/4
Остается решить систему уравнений:
у=24, х=12
Ответ: 1 оператор за 12 ч, 2 оператор за 24 ч.
Слайд 17
Чтобы накачать в бак 117 л воды, требуется
на 5 минут больше времени, чем на то, чтобы
выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Решение: Пусть за минуту в бак накачивается х литров воды.
По условию задачи составим уравнение:
х≠0, х≠-3
117(х+3)-96х=5х(х+3)
117х+351-96х=5 +15х
- 6х - 351=0
х=9 и х = -7,8( не удовлетворяет условию задачи)
Ответ: 9 литров.
Слайд 18
Задачи на проценты, смеси , сплавы
Слайд 19
Основными компонентами в этих задачах являются:
масса раствора (смеси, сплава);
масса вещества;
доля (% содержание) вещества
Слайд 20
Теоретические сведения
m1 – масса первой смеси (сплава)
m2
– масса второй смеси (сплава)
р1 – концентрация некоторого вещества
в первой смеси (сплаве)
р2 - концентрация этого вещества во второй смеси (сплаве)
р – концентрация этого вещества в новой смеси (сплаве)
m1+m2 масса новой смеси (сплава)
р1m1+р2m2=р(m1+m2)
Слайд 21
Таблица для решения задач имеет следующий вид
Слайд 22
Задача 1. Смешали 4 л 15%-ного раствора соли
с 5 л 20%-ного соли к смеси добавили 1
л чистой воды. Какова концентрация полученной смеси?
Уравнение для решения задачи имеет вид:
0,15·4 + 0,2·5=0,01х·10
0,1х = 1,6
х = 16
Ответ: концентрация смеси 16 %.
Слайд 23
Задача 2. Смешав 40 % и 15 %
растворы кислоты, добавили 3 кг чистой воды и получили
20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 %раствора той же кислоты, то получили бы 50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 %растворов кислоты было смешано?
Получаем уравнение:0,4х + 0,15у = 0,2(х + у +3)
Слайд 24
Задача 2. Смешав 40 % и 15 %
растворы кислоты, добавили 3 кг чистой воды и получили
20 % раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80 %раствора той же кислоты, то получили бы 50 %-ый раствор кислоты. Сколько килограммов 40 % -го и 15 %растворов кислоты было смешано?
0,4х + 0,15у + 0,8·3 = 0,5(х + у +3).
Слайд 25
Для решения задачи получаем систему уравнений:
Решаем систему уравнений:
Ответ:3,4
кг 40 % кислоты и 1,6 кг 15 %
кислоты.
Слайд 26
Задача 3. Имеется три сосуда. В первый сосуд
налили 4 кг 70 % сахарного сиропа, а во
второй – 6 кг 40 % сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55 % содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35 % содержание сахара. Найдите массу сахарного сиропа в третьем сосуде сиропа и концентрацию сахара в нем.
Слайд 27
Итак, получаем систему уравнений :
Решаем её:
Ответ :1,5 кг
сахарного сиропа 15 % концентрации.
Слайд 28
Задача 4. Сплав меди и олова массой 10
кг содержит 70% олова. К этому сплаву добавили 8
кг меди. Сколько нужно добавить килограмм олова, чтобы его концентрация стала в 3 раза больше, чем концентрация меди?
Пусть концентрация меди равна t%, тогда концентрация олова 3t%,
так как суммарная концентрация меди и олова должна быть равной 100% (других компонентов в сплаве нет), имеем уравнение t + 3t = 100, откуда концентрация меди равна 25%, а концентрация олова равна 75%.
7+х=0,75(18+х)
х = 26.
Ответ: 26 кг.
Слайд 29
Задача 5. Первоначально влажность зерна составляла 25%. После
того как 200 кг зерна просушили, оно потеряло в
массе 30 кг. Вычислить влажность просушенного зерна.
Составляем уравнение:
50-30=1,7х
Ответ: 11,8%.
Слайд 30
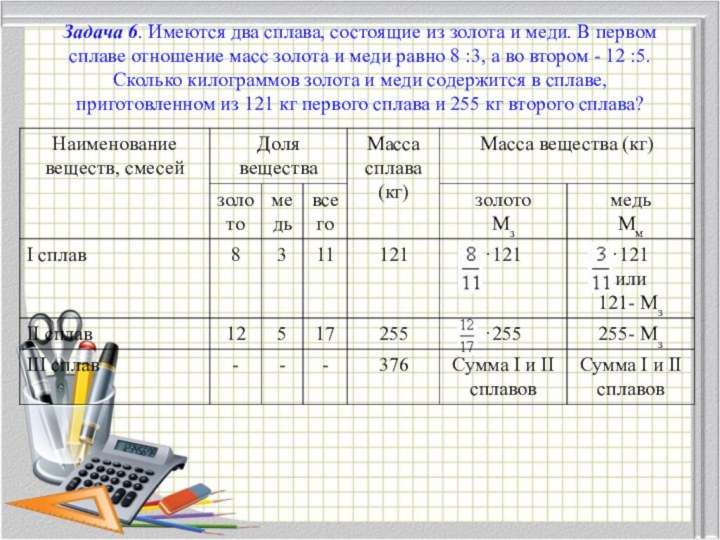
Задача 6. Имеются два сплава, состоящие из золота
и меди. В первом сплаве отношение масс золота и
меди равно 8 :3, а во втором - 12 :5. Сколько килограммов золота и меди содержится в сплаве, приготовленном из 121 кг первого сплава и 255 кг второго сплава?
Слайд 31
·121 = 88 (кг) – масса золота в
I сплаве
·255 = 180 (кг) масса золота в II
сплаве
121+255=376 (кг) – масса III сплава
88+180=268 (кг) -масса золота в III сплаве
376-268=108 (кг) масса меди в III сплаве
Ответ :268 кг золота и 108 кг меди.
Слайд 32
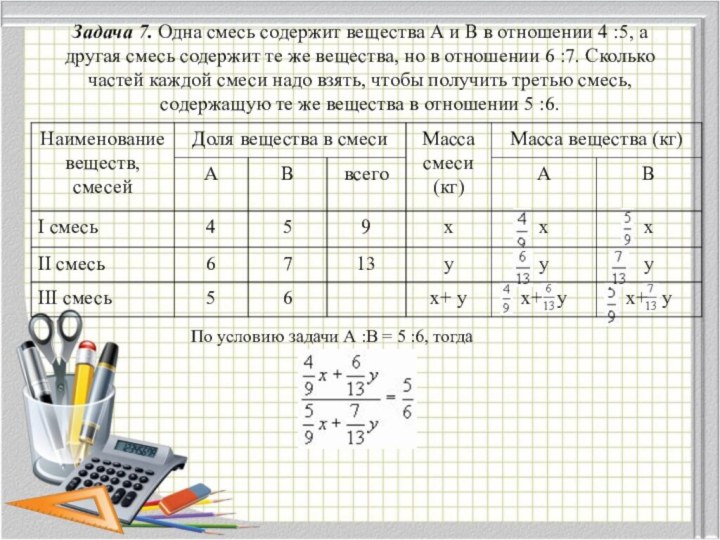
Задача 7. Одна смесь содержит вещества А и
В в отношении 4 :5, а другая смесь содержит
те же вещества, но в отношении 6 :7. Сколько частей каждой смеси надо взять, чтобы получить третью смесь, содержащую те же вещества в отношении 5 :6.
По условию задачи А :В = 5 :6, тогда
Слайд 33
Решаем уравнение относительно
.Получим
=
.
Ответ : 9 частей
первой смеси и 13 частей второй смеси.
Слайд 34
Предлагаемый подход к решению текстовых задач с помощью
уравнений сводится к следующему:
1.Через х обозначаем меньшую величину
или то, о чём спрашивается в вопросе задачи.
2.Краткую запись оформляем в виде таблицы, схемы.
3.По условию задачи заполняем 2 столбика задачи, третий столбик нам даёт уравнение.
4.Смотрим, к какому типу относится задача (на сложение величин, на сравнение и т.п.) в зависимости от этого составляем уравнение.
5.Найдя х, смотрим, ответили мы на вопрос задачи, или нет, если нет, то решаем и находим ответ.