Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Комплексные числа в алгебраической форме

Содержание

Действия с комплексными числами в алгебраической форме
Комплексные числаКомплексные числаКомплексные числа Действия с комплексными числами в алгебраической форме СложениеПравило сложениякомплексных чисел Сложение ВычитаниеПравило вычитаниякомплексных чисел Вычитание Сложение и вычитение УмножениеПравило умножениякомплексных чисел УмножениеОднако при умножении комплексных чисел следует помнить, что математики с XVI века Умножение Умножение ДелениеПравило делениякомплексных чиселЧастным от деления комплексного числа z1=a1+b1i на число z2=a2+b2i ≠ Деление Деление Деление Умножение и деление Умножение и деление
Слайды презентации

Слайд 2

Слайд 3 Действия с комплексными
числами в алгебраической форме

Действия с комплексными числами в алгебраической форме

Слайд 4 Сложение
Правило сложения
комплексных чисел

СложениеПравило сложениякомплексных чисел

Слайд 5 Сложение

Сложение

Слайд 6 Вычитание
Правило вычитания
комплексных чисел

ВычитаниеПравило вычитаниякомплексных чисел

Слайд 7 Вычитание

Вычитание

Слайд 8 Сложение и вычитение

Сложение и вычитение

Слайд 9 Умножение
Правило умножения
комплексных чисел

УмножениеПравило умножениякомплексных чисел

Слайд 10 Умножение
Однако при умножении комплексных чисел
следует помнить, что

УмножениеОднако при умножении комплексных чисел следует помнить, что математики с XVI

математики с XVI века
производили операции над этими числами

по
тем же правилам, что и над многочленами,
учитывая, что i2 =-1

Слайд 11 Умножение

Умножение

Слайд 12 Умножение

Умножение

Слайд 13 Деление
Правило деления
комплексных чисел
Частным от деления комплексного числа z1=a1+b1i

ДелениеПравило делениякомплексных чиселЧастным от деления комплексного числа z1=a1+b1i на число z2=a2+b2i


на число z2=a2+b2i ≠ 0, называется комплексное число
z3

= a3+b3i, такое, что z1 = z2∙z3.

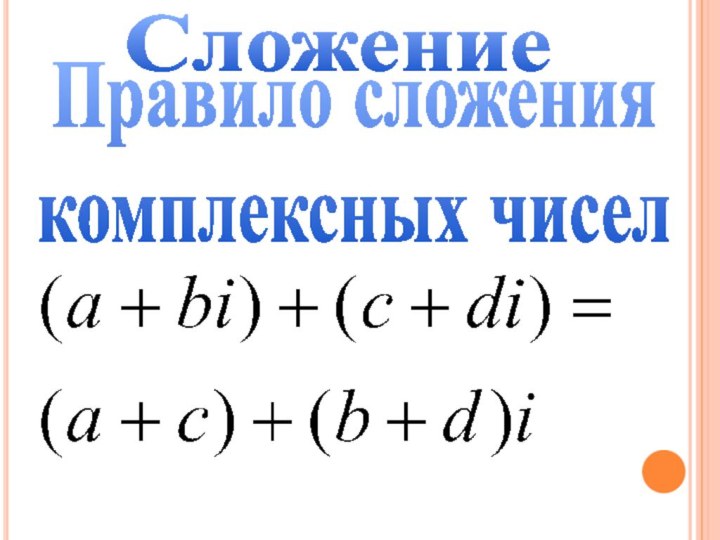
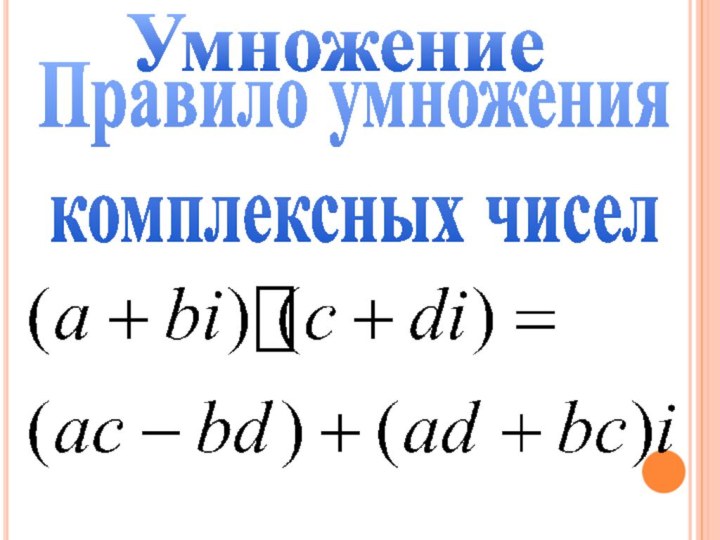
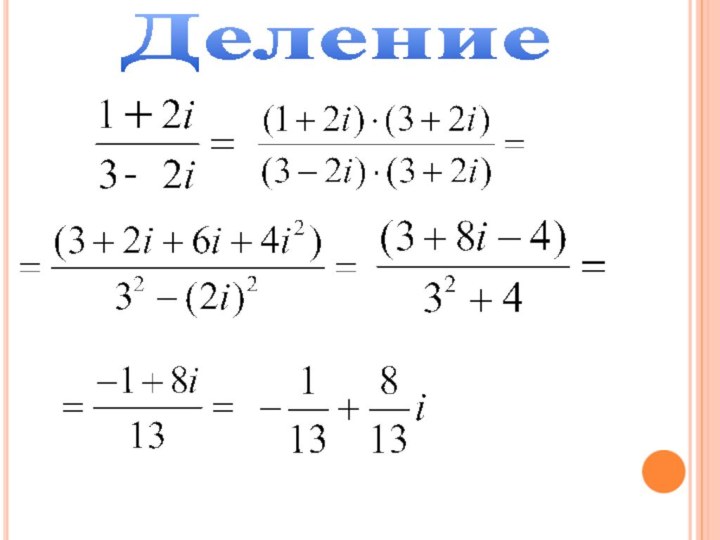
Это равенство легко получить путем умножения числителя и знаменателя дроби на число комплексно – сопряженное знаменателю.

Слайд 14 Деление

Деление

Слайд 15 Деление

Деление

Слайд 16 Деление

Деление

Слайд 17 Умножение и деление

Умножение и деление
  • Имя файла: kompleksnye-chisla-v-algebraicheskoy-forme.pptx
  • Количество просмотров: 136
  • Количество скачиваний: 0
- Предыдущая Презентация по развитию речи Весна (6 класс)
Следующая - Презентация Развитие жизни на Земле

Похожие презентации

Решить уравнение Решить уравнение 125
Приёмы устного решения квадратного уравнения Приёмы устного решения квадратного уравнения 140
Функция y = x^2 Функция y = x^2 156
ПРезентация Интегрированный урок по алгебре и географии ПРезентация Интегрированный урок по алгебре и географии 165
Понятие предела функции Понятие предела функции 229
Квадратные уравнения Квадратные уравнения 129
Модуль Модуль 139
Определение арифметической прогрессии Определение арифметической прогрессии 157
Методы решения логарифмических уравнений Методы решения логарифмических уравнений 136
Презентация по алгебре на тему Пик знаний Презентация по алгебре на тему Пик знаний 83
Презентация к проекту Логарифмы - прихоть математиков или жизненная необходимость Презентация к проекту Логарифмы - прихоть математиков или жизненная необходимость 271
Элементы математической статистики Элементы математической статистики 157
Презентация по математике на тему Подготовка к сдаче ГИА, решение уравнений Презентация по математике на тему Подготовка к сдаче ГИА, решение уравнений 170
Показательная функция Показательная функция 79
Презентация математической викторины Умники и умницы Презентация математической викторины Умники и умницы 157
Формулы радиусов вписанного и описанного кругов треугольника Формулы радиусов вписанного и описанного кругов треугольника 167
Подобные слагаемые 7 класс Подобные слагаемые 7 класс 169
Презентация по алгебре на тему Решение квадратных уравнений Презентация по алгебре на тему Решение квадратных уравнений 164
Презентация по математике на тему: Делимость. Свойства делимости (8 класс) Презентация по математике на тему: Делимость. Свойства делимости (8 класс) 180
Презентация к диплому Развитие критического мышления на уроках математики в 8 классе Презентация к диплому Развитие критического мышления на уроках математики в 8 классе 164
Уравнение и его корни Уравнение и его корни 150
Презентация к уроку Применение различных способов разложения многочленов на множители (7 класс) Презентация к уроку Применение различных способов разложения многочленов на множители (7 класс) 167
Внеклассный урок по алгебре 7 класс с казахским языком обучения Внеклассный урок по алгебре 7 класс с казахским языком обучения 245
Презентация к внеклассному мероприятию Виртуальная экскурсия Морис Эшер - художник или математик... Презентация к внеклассному мероприятию Виртуальная экскурсия Морис Эшер - художник или математик... 179
Свойства функции y=sin(x) и ее график Свойства функции y=sin(x) и ее график 162
Урок обобщающего повторения на тему Треугольник в 9 классе Урок обобщающего повторения на тему Треугольник в 9 классе 57
Шаблоны презентаций Математика - 7 Шаблоны презентаций Математика - 7 75
Презентация к проекту Мой край родной в математических задачах Презентация к проекту Мой край родной в математических задачах 223
Презентация по математике на тему Квадратные уравнения (8 класс) Презентация по математике на тему Квадратные уравнения (8 класс) 225
Исследование функции с помощью производной Исследование функции с помощью производной 154