- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре на тему Разложение многочлена на множители
Содержание
- 2. Задание 1. Соединить линиями соответствующие части определения:
- 3. Задание 2. Закончите определениеПредставление многочлена в виде
- 4. Задание 3. Восстановить порядок выполнения действий при
- 5. Задание 4. Отметить знаком «+» верные выраженияа)
- 6. Вынесение общего множителя за скобкиФормулы сокращенного умноженияСпособ
- 8. Ответы
- 9. 1. Вынести общий множитель за скобку (если
- 10. Вынесение общего множителя за скобкуИз каждого слагаемого,
- 11. Группировка Бывает, что члены многочлена не имеют
- 12. Применение формул сокращенного умножения Группа из двух,
- 13. Задание 4. Разложить многочлен на множители и
- 14. Скачать презентацию
- 15. Похожие презентации
Задание 1. Соединить линиями соответствующие части определения:

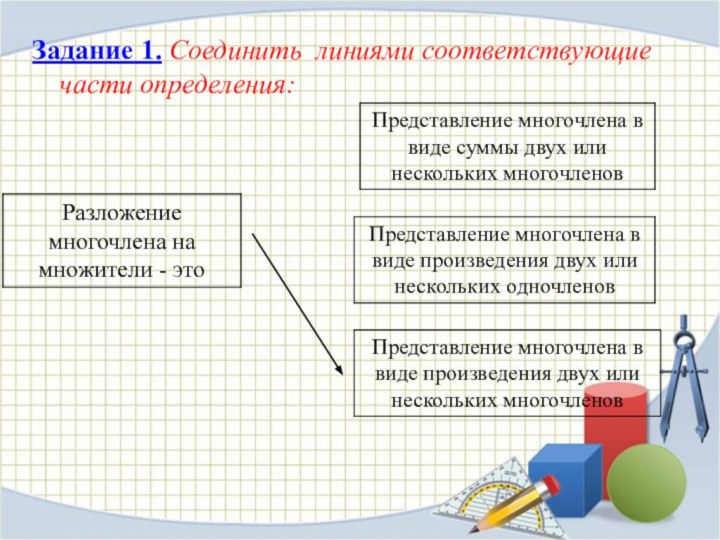












Слайд 3
Задание 2. Закончите определение
Представление многочлена в виде произведения
одночлена и многочлена называется ….
скобкиСлайд 4 Задание 3. Восстановить порядок выполнения действий при разложении
многочлена на множители способом группировки.
Вынести в каждой группе общий множитель (в виде многочлена) за скобки
Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель
Вынести в каждой группе общий множитель в виде одночлена за скобки
1
2
3
Слайд 5
Задание 4. Отметить знаком «+» верные выражения
а) а2
+ в2 - 2ав = ( а – в
)2б) m2 + 2mn – n2 = ( m – n)2
в) 2pt – p2 – t2 = ( p – t )2
г) 2cd + c2 + d2 = ( c + d )2
+
+
Слайд 6
Вынесение общего множителя за скобки
Формулы сокращенного умножения
Способ группировки
20х3у2
+ 4 х2у
в(а + 5 ) – с
( а + 5 ) 15а3в + 3а2в3
2у ( х – 5 ) + х ( х – 5 )
а4 – в4
27 в3 + а6
х2 + 6х + 9
49m – 25 n
2вх – 3ау – 6ву + ах
а + ав – 5а – 5в
2 аn -5 bn – 10 bn + am
3a + 3ab – 7a – 7b
Метод разложения на множители
Слайд 9
1. Вынести общий множитель за скобку (если он
есть).
2. Попробовать разложить многочлен на множители по формулам сокращенного
умножения.3. Попытаться применить способ группировки (если предыдущие способы не привели к цели).
Слайд 10
Вынесение общего множителя за скобку
Из каждого слагаемого, входящего
в многочлен, выносится некоторый одночлен, входящий в качестве множителя
во все слагаемые.Таким общим множителем может быть не только одночлен, но и многочлен.
Слайд 11
Группировка
Бывает, что члены многочлена не имеют общего
множителя, но после заключения нескольких членов в скобки (на
основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.
Слайд 12
Применение формул сокращенного умножения
Группа из двух, трех
(или более) слагаемых, которая обращает выражение, входящее в одну
из формул сокращенного умножения, заменяется произведением многочленов.Слайд 13 Задание 4. Разложить многочлен на множители и указать,
какие приемы использовались при этом
Пример 1. 36а6в3 – 96а4в4
+ 64 а2в5. Пример 2. а2 + 2ав + в2 – с2.
Пример 3. у3 - 3у2 + 6у – 8.
(у – 2)(у2 – у + 4).
(а + в – с)(а + в +с).
4а2в3(3а2 – 4в)2