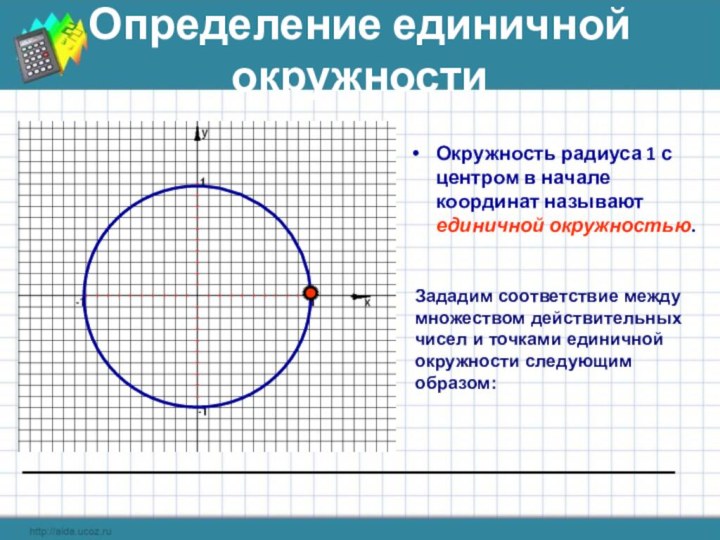
дугу окружности длиной в один радиус (обозначается 1 рад).
1 рад
R
R
R
A
B
O
AB=R
AOB=1 рад
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть










1 рад
R
R
R
A
B
O
AB=R
AOB=1 рад
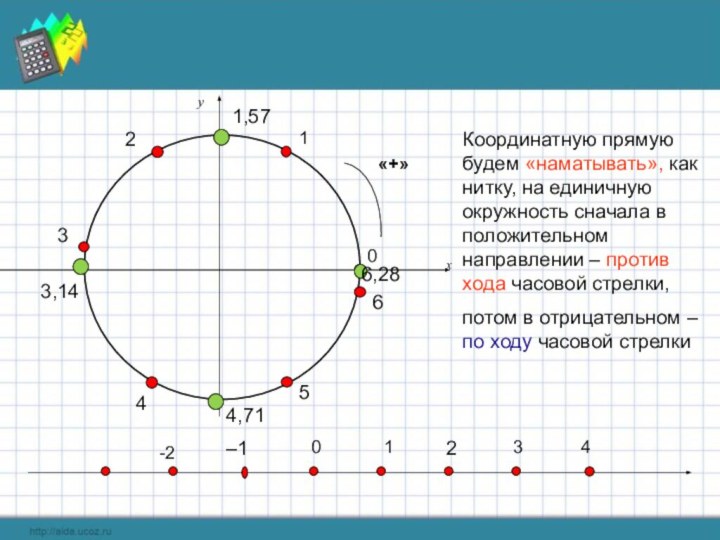
«+»
x
y
0
Угол поворота можно измерить двумя мерами : градусной и радианной
О
«+»
«-»
x = cos α y = sinα
x
y
0
1
1
0
A(α)
A(α+2)
x
y
0
1
1
0
72⁰
I
II
III
IV
3,6
5,1
210⁰
478⁰=
782⁰=
360⁰+ 118⁰
2*360⁰+ 42⁰
478⁰
782⁰
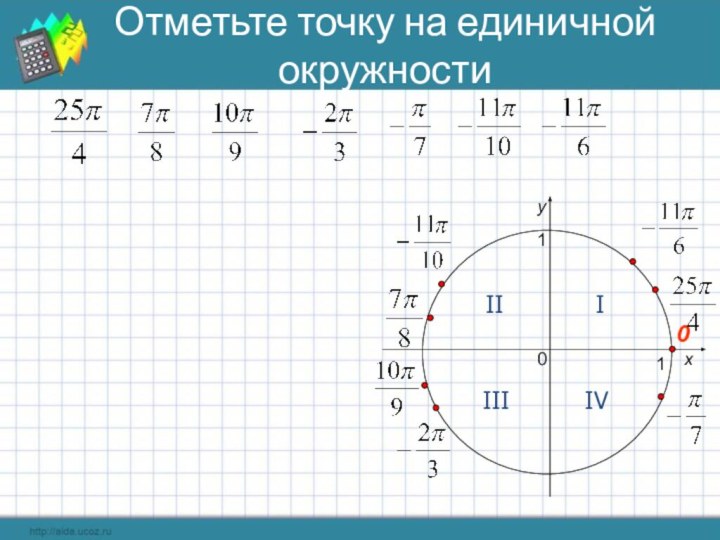
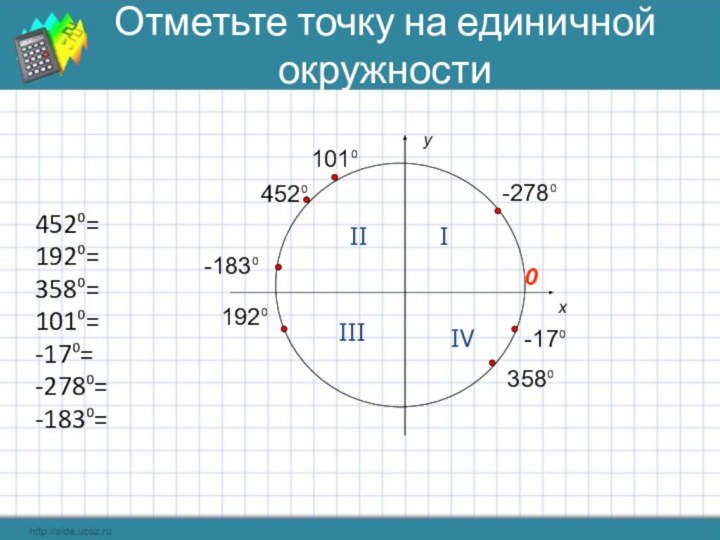
Отметьте точку на единичной окружности
452⁰
192⁰
101⁰
-17⁰
-278⁰
-183⁰