- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к проекту Эта удивительная парабола!
Содержание
- 2. «Что чувство удивления – могучий источник желания
- 3. Цели исследования: Изучить некоторые свойства квадратичной функции
- 4. Основными этапами исследования были:-постановка проблемы,-сбор материала,-проведение опытов
- 5. 1.1Парабола в древности и до наших дней.
- 6. Аполоний Пергский
- 7. «Парабола” означает приложение или притча. Долгое время
- 8. II. Практическое применение параболы. 1.В технике. Если парабола
- 10. На этом свойстве основано конструирование автомобильных фар,
- 11. Параболы в окружающем мире. Космос Параболическая скорость
- 12. Некоторые космические тела, такие как кометы или
- 13. Для тренировок будущих космонавтов на земле проводятся
- 14. 2. В медицине. В медицине используется параболическое
- 16. 4. В архитектуре. Параболические формы
- 17. Ворота Сент-Луиса в Миссури
- 18. 1.2 Изучение квадратичной функции. Построение параболы. Первый способ.
- 19. Второй способ. Прямая DD1 -директриса. Точка F - фокус
- 20. Рене Декарт(1596- 1650г.г.) Пьер Ферма(1601- 1665г.г)
- 21. Лейбниц (1646-1716г.г.) Иоганн Бернулли(1667- 1748 г.г)
- 22. Функция y=ax²+bx+c, где a, b, c
- 23. Исследовательская работа Цель: выяснить как коэффициенты а,
- 24. Вывод: график функции у =- х2 можно
- 25. Исследование 2Мы заметили что, график стал уже.
- 26. Исследование 3График данной функции стал шире по
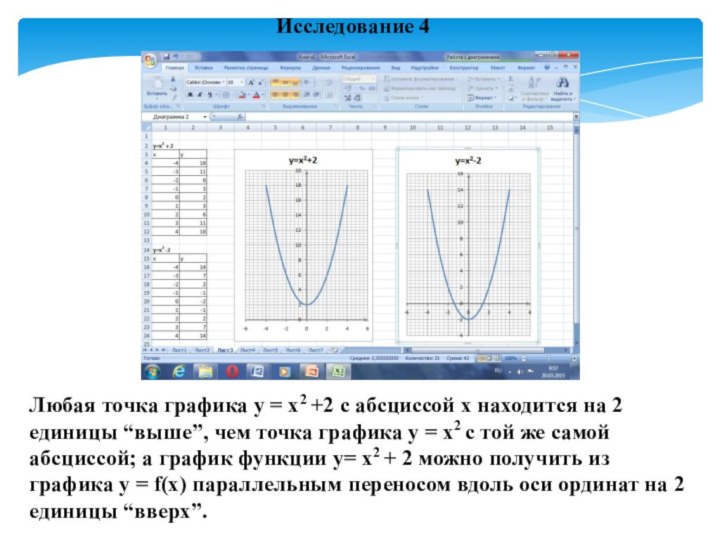
- 27. Исследование 4Любая точка графика y = х2
- 28. График функции y=f(x+m) можно получить из графика
- 29. 1.Построить график функции у=|a|x2 (по точкам)..Если а0, и вправо, если m0,и вниз, если n
- 30. Исследование 61.График симметричен графику функции у=х2 относительно
- 31. Выводы:Изучили значимость творческого опыта в области алгебры
- 32. На первый взгляд, понятие не ново,И не
- 33. Скачать презентацию
- 34. Похожие презентации






























Слайд 2 «Что чувство удивления – могучий источник желания знать:
от удивления к знаниям – один шаг»
В.А. Сухомлинский.Слайд 3 Цели исследования: Изучить некоторые свойства квадратичной функции особенности ее
графика.
Объект исследования:
Предмет исследования:
Задачи исследования: Как влияют разные коэффициенты на внешнюю форму параболы
Квадратичная функция, парабола.
Изучить роль математики в развитии цивилизации и культуры.
Ознакомиться с оптическими свойствами параболы, рассмотреть их применение в технике, быту.
Изучить некоторые свойства квадратичной функции.
Исследовать квадратичную функцию; составить алгоритм построения графика квадратичной функции, основываясь на её свойствах.
Слайд 4
Основными этапами исследования были:
-постановка проблемы,
-сбор материала,
-проведение опытов по
построению квадратичной функции и параболы.
В своей работе мы использовали
следующие методы:1) сбор и анализ литературы по теме;
2) сравнение;
3) обобщение;
4) работа с помощью программы Microsoft Office Excel.
Слайд 7 «Парабола” означает приложение или притча. Долгое время так
называли линию среза конуса, пока не появилась квадратичная функция.
Слайд 8 II. Практическое применение параболы. 1.В технике. Если парабола вращается вокруг оси
z, то получается бесконечная «чаша», называемая параболоидом вращения.
Слайд 10 На этом свойстве основано конструирование автомобильных фар, прожекторов,
параболических антенн и других устройств с отражающими поверхностями, имеющими
формы параболоидов.Слайд 11 Параболы в окружающем мире. Космос Параболическая скорость — это скорость
относительного движения двух тел, взаимно притягивающихся по закону всемирного
тяготения, при которой движение происходит по параболической орбите.Слайд 12 Некоторые космические тела, такие как кометы или астероиды,
имеют траекторию движения в форме параболы. Скорость , с
которой двигаются эти тела, называется параболической или космической скоростью .
Слайд 13
Для тренировок будущих космонавтов на земле проводятся специальные
полеты самолетов по траектории параболы, чем достигается эффект невесомости
в гравитационном поле земли.
Слайд 14
2. В медицине.
В медицине используется параболическое устройство, за
счет которого удается разрушить камень в почках.
Слайд 16 4. В архитектуре. Параболические формы можно встретить в
архитектурных сооружениях.
Площадь святого
Петра в Ватикане.Собор Санта-Мария-дель-Фьоре во Флоренции
Слайд 22
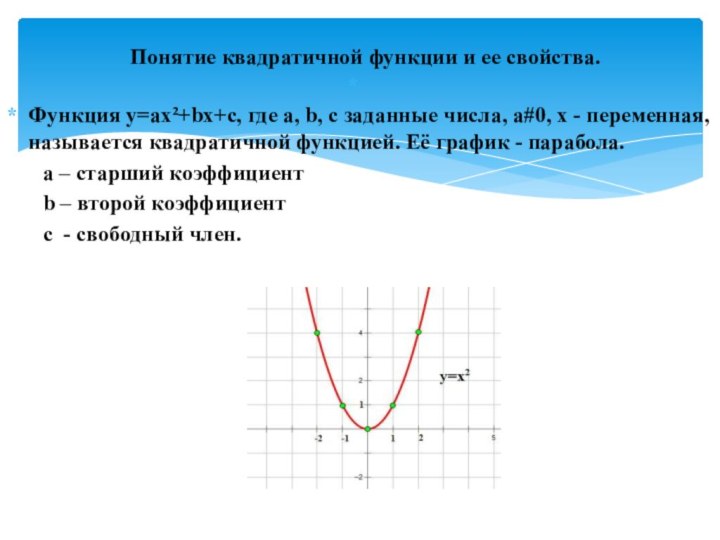
Функция y=ax²+bx+c, где a, b, c заданные
числа, a#0, x - переменная, называется квадратичной функцией. Её
график - парабола.a – старший коэффициент
b – второй коэффициент
с - свободный член.
Понятие квадратичной функции и ее свойства.
Слайд 23
Исследовательская работа
Цель: выяснить как коэффициенты а, m,
n влияют на внешнюю форму графика функции на математической
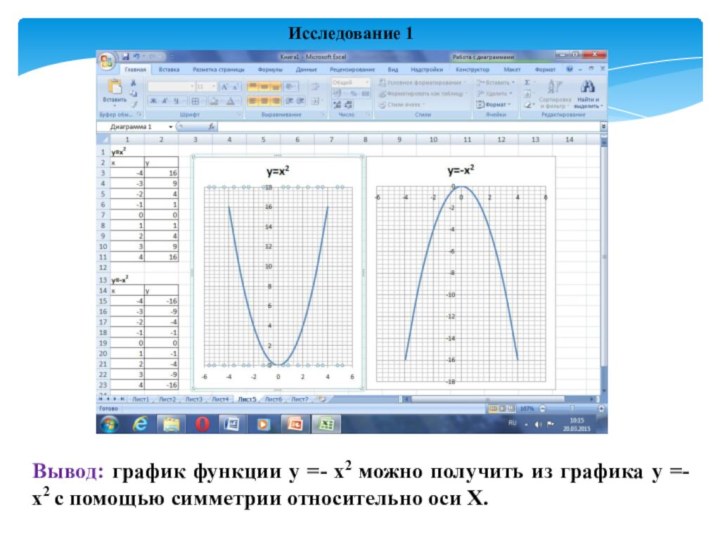
модели квадратичной функции у=а(х+m)2 + n, используя программу Microsoft Office Excel.Слайд 24 Вывод: график функции у =- х2 можно получить
из графика у =- х2 с помощью симметрии относительно
оси Х.Исследование 1
Слайд 25
Исследование 2
Мы заметили что, график стал уже. Из
построенного графика мы видим, что парабола растягивается относительно оси
абсцисс. А такое преобразование на математическом языке называется - растяжением.
Слайд 26
Исследование 3
График данной функции стал шире по отношению
с основным графиком. А такое преобразование на математическом языке
называется - сжатием графика.
Слайд 27
Исследование 4
Любая точка графика y = х2 +2
с абсциссой х находится на 2 единицы “выше”, чем
точка графика y = х2 с той же самой абсциссой; а график функции y= х2 + 2 можно получить из графика y = f(x) параллельным переносом вдоль оси ординат на 2 единицы “вверх”.Слайд 28 График функции y=f(x+m) можно получить из графика функции
y=f(x), «сдвинув» его на |m| единиц в право вдоль
оси абсцисс, если m<0, и на |m| единиц влево вдоль оси абсцисс, если m>0.Исследование 5
Слайд 29
1.Построить график функции у=|a|x2 (по точкам).
.Если а
осевую симметрию относительно оси OX.
3.Осуществить сдвиг графика вдоль оси
OX на |m| единиц масштаба влево, если m>0, и вправо, если m<0.4.Осуществить сдвиг полученного графика вдоль оси OY на |n| единиц масштаба вверх, если n>0,и вниз, если n<0.
Алгоритм построения графика функции у=а(х+m)2 + n
Слайд 30
Исследование 6
1.График симметричен графику функции у=х2 относительно оси
ОХ Ветви направлены вниз.
2.Сжатие графика в 2 раза
3.График сдвинут
на 4 единицы вправо.4.График сдвинут на 7 единиц вверх.
Слайд 31
Выводы:
Изучили значимость творческого опыта в области алгебры на
примерах практического применения свойств данной кривой в различных сферах
деятельности человека.В процессе нашей работы мы познакомились с историей открытия параболы, углубили свои знания о различных её свойствах, о способах построения.
Слайд 32
На первый взгляд, понятие не ново,
И не всегда
подумаешь о том,
Как важно будет в жизни это слово
И
сколько смысла будет в слове том!По- разному с годами толковали.
Сам Лобачевский руку приложил,
Чтоб слово «функция» и в средней школе знали,
Чтоб каждый ученик им дорожил!