- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Неравенства и их системы.
Содержание
- 2. 1). Определение 2). Виды 3). Свойства
- 3. Запись вида а>в или а
- 4. Неравенства вида а≥в, а≤в называются ……Неравенства вида а>в, а
- 5. 1). Если а>в, то вв, в>с, то
- 6. 1). Любой член неравенства можно переносить из
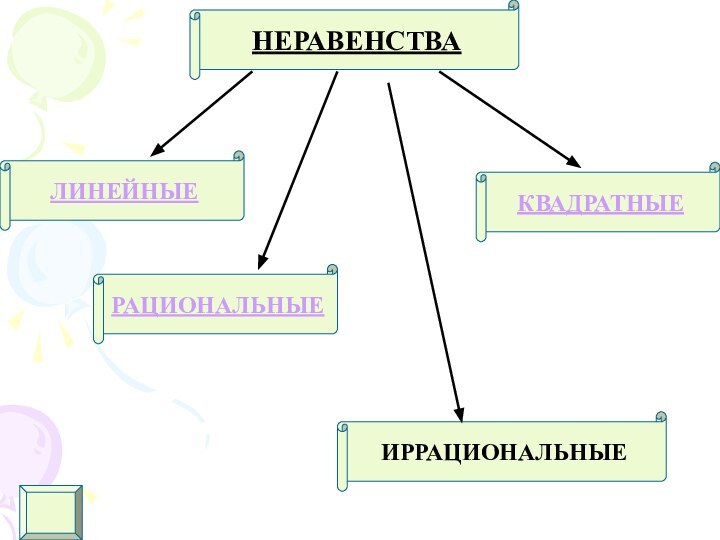
- 7. ЛИНЕЙНЫЕКВАДРАТНЫЕРАЦИОНАЛЬНЫЕИРРАЦИОНАЛЬНЫЕНЕРАВЕНСТВА
- 8. I).I).Линейное неравенство.2х+4≥6; х
- 9. 1.Решить неравенства.1). х+2≥2,5х-1;2).х- 0,25(х+4)+0,5(3х-1)>3;3).4).х²+х
- 10. Найдите наименьшие целые числа, являющиеся решениями неравенств1.2(х-3)-1-3(х-2)-4(х+1)>0;2.0,2(2х+2)-0,5(х-1)
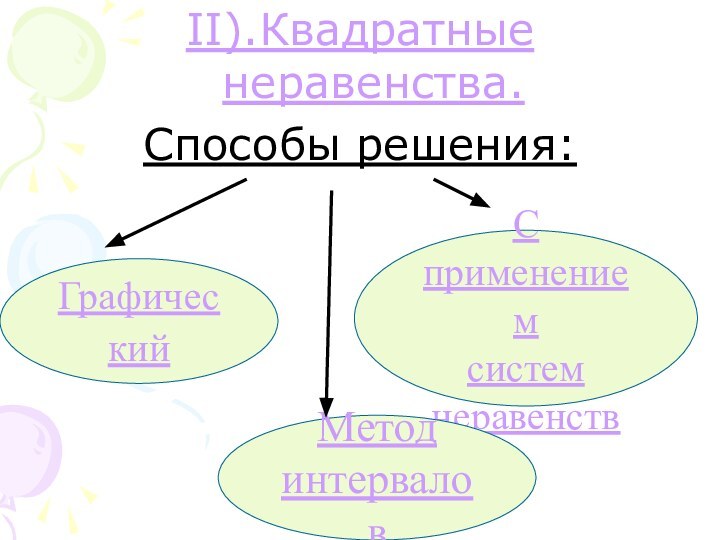
- 11. II).Квадратные неравенства.Способы решения:Графический С применением систем неравенствМетод интервалов
- 12. 1.1).Метод интервалов(для решения квадратного уравнения)
- 13. x²+x-6=0; (х-2)(х+3)=0; Ответ: (-∞;-3)v(2;+∞).
- 14. 1.Решение неравенства методом интервалов.1). х(х+7)≥0;2).(х-1)(х+2)≤0;3).х-х²+20;5).х(х+2)
- 15. Домашняя работа:Сборник 1).стр. 109 № 128-131Сборник 2).стр.111 №3.8-3.10; 3.22;3.37-3.4
- 16. 1.2).Решение квадратных неравенств графически1). Определить направление ветвей
- 17. Пример:х²+5х-6≤0y= х²+5х-6 (квадратичная функция, график парабола, а=1,
- 18. Решите графически неравенства:1).х²-3х0;3).х²+2х≥0;4). -2х²+х+1≤0;(0;3)(-∞;0)U(4;+∞)(-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞)
- 19. Домашнее задание:Сборник 1).стр. 115 №176-179.
- 20. III).Рациональные неравенства вида решают методом интервалов.1) Раскладывают
- 21. Сборник 1).стр. 109 №132Сборник 2). Стр. 112-113
- 22. Системы неравенств.
- 23. 1). Содержащие линейные неравенства.2). Содержащие квадратное(рациональное) неравенство
- 24. 1). 5х+1>6 5x>5 x>1 2x-4
- 25. 2). х²-1>0 (x-1)(x+1)>0 x+4
- 26. 3). х²-4>0 x²-3x+5
- 27. 4). -12
- 29. Скачать презентацию
- 30. Похожие презентации
1). Определение 2). Виды 3). Свойства числовых неравенств 4). Основные свойства неравенств 4). Типы 5). Способы решения










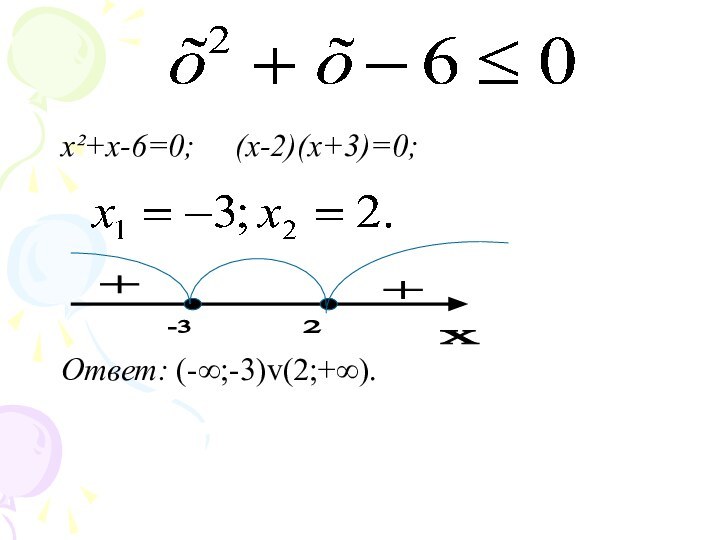




![Неравенства и их системы. Решите графически неравенства:1).х²-3х0;3).х²+2х≥0;4). -2х²+х+1≤0;(0;3)(-∞;0)U(4;+∞)(-∞;-2]U[0;+∞) (-∞;-0,5]U[1;+∞)](/img/tmb/12/1195952/fe4d74d1864bcf9e0afe04e0ac4351a9-720x.jpg)











Слайд 5
1). Если а>в, то вв, в>с, то
а>с.
3). Если а>в, с-любое число, то а+с>в+с.
4). Если а>в,
с>х, то а+с>в+х.5). Если а>в, с>0, то ас>вс.
6). Если а>в, с<0, то ас<вс.
8). Если а>о, с>0, а>с, то >
Слайд 6
1). Любой член неравенства можно переносить из одной
части неравенства в другую, изменив его знак на противоположный,
при этом знак неравенства не меняется.2).Обе части неравенства можно умножить или разделить на одно и тоже положительное число, при этом знак неравенства не изменится. Если это число отрицательное, то знак неравенства изменится на противоположное.
Слайд 10
Найдите наименьшие целые числа, являющиеся решениями неравенств
1.2(х-3)-1-3(х-2)-4(х+1)>0;
2.0,2(2х+2)-0,5(х-1)
натуральные числа, являющиеся решениями неравенства
3х-3
Слайд 11
II).Квадратные неравенства.
Способы решения:
Графический
С применением
систем
неравенств
Метод
интервалов
Слайд 12
1.1).Метод интервалов
(для решения квадратного уравнения)
ах²+вх+с>0
1). Разложим данный многочлен на множители,
т.е. представим в виде а(х- )(х- )>0.
2).корни многочлена нанести на числовую ось;
3). Определить знаки функции в каждом из промежутков;
4). Выбрать подходящие интервалы и записать ответ.
Слайд 16
1.2).Решение квадратных неравенств графически
1). Определить направление ветвей параболы,
по знаку первого коэффициента квадратичной функции.
2).Найти корни соответствующего квадратного
уравнения;3).Построить эскиз графика и по нему определить промежутки, на которых квадратичная функция принимает положительные или отрицательные значения.
Слайд 17
Пример:
х²+5х-6≤0
y= х²+5х-6 (квадратичная функция, график парабола, а=1, ветви
направлены вверх)
х²+5х-6=0; корни уравнения: 1 и -6.
у+ +
-6 1 x
Ответ: [-6;1].
-
Слайд 18
Решите графически неравенства:
1).х²-3х0;
3).х²+2х≥0;
4). -2х²+х+1≤0;
(0;3)
(-∞;0)U(4;+∞)
(-∞;-2]U[0;+∞)
(-∞;-0,5]U[1;+∞)
Слайд 19
Домашнее задание:
Сборник 1).стр. 115 №176-179.
работы №47,45,42,17,12
(задание №5)Сборник 2).стр. 116 № 4.4,4.5, 4.11.
работы №6, задание 13.
Слайд 20
III).Рациональные неравенства вида
решают методом интервалов.
1) Раскладывают на линейные
множители числитель P(x) и знаменатель Q(x). Если это удается,
то дальше поступают так.2) На числовую ось наносят корни всех линейных множителей. На каждом из промежутков, на которые эти точки разбивают ось, дробь P(x)/ Q(x). сохраняет знак
3) Определяют знак дроби на каждом промежутке.
4) Записывают ответ.
Слайд 23
1). Содержащие линейные неравенства.
2). Содержащие квадратное(рациональное) неравенство и
линейное неравенство.
3). Содержащие квадратные неравенства.
4). Двойное неравенство, которое решается
с помощью систем.5). Неравенства с модулем
Слайд 24
1). 5х+1>6 5x>5
x>1
2x-4
2x<7 ; x<3,5.1 3,5 x
Ответ: (1;3,5).
Задания:
Сборник 1). Стр. 111№139-142
стр. 170-172 № 711-766
Сборник 2).стр. 110 № 3.4-3.7
Слайд 25
2). х²-1>0 (x-1)(x+1)>0
x+4
+ - +-4 -1 1 x
Ответ: (-∞;-4).
Задания:
Сборник 1).стр. 111 № 143-145
Сборник 2). Стр. 112-113 №3.24, 3.25
Слайд 26
3). х²-4>0
x²-3x+5
квадратное неравенство в отдельности. Изображаем решения на числовой прямой
и смотрим пересечения этих решений. Записываем ответ.Задания:
Сборник 1). Стр. 111 № 146-147
Сборник 2).стр. 113, 115 № 3.27, 3.29,
3.47, 3.48
Слайд 27
4). -12
x
x-1>-12; x>-11.
Ответ: (-11;2).
Задания:
Сборник 1).стр. 109 № 126-127, 134,
стр. 172 №783-790
Сборник 2). Стр. 111 №3.9