- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Статистика (11 класс)
Содержание
- 2. Статистика(лат. «status») состояние делСтатистика — это точная
- 3. Статистика(лат. «status») состояние делМатематическая статистика – это
- 4. Статистика(лат. «status») состояние делСтатистика имеет дело со
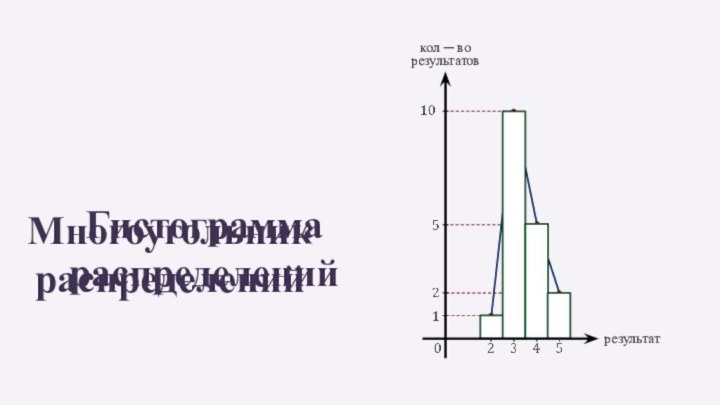
- 5. результаткол ─ ворезультатовМногоугольникраспределенийГистограммараспределений
- 6. Круговаядиаграмма
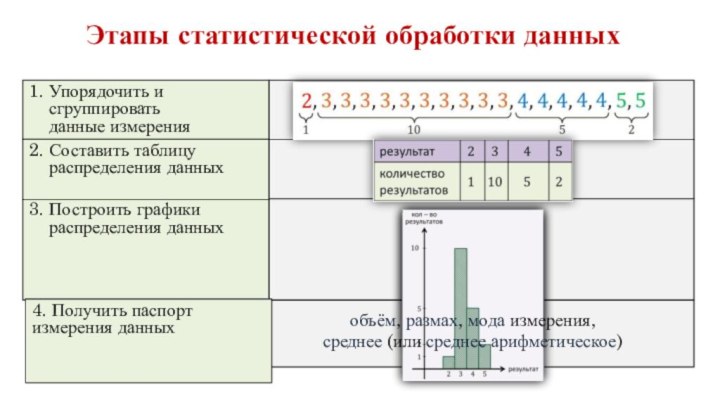
- 7. Этапы статистической обработки данных3. Построить графики распределения
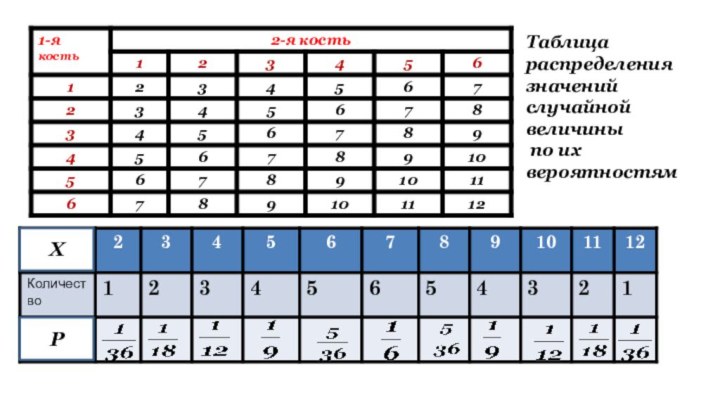
- 8. ХРТаблица распределения значений случайной величины по их вероятностям
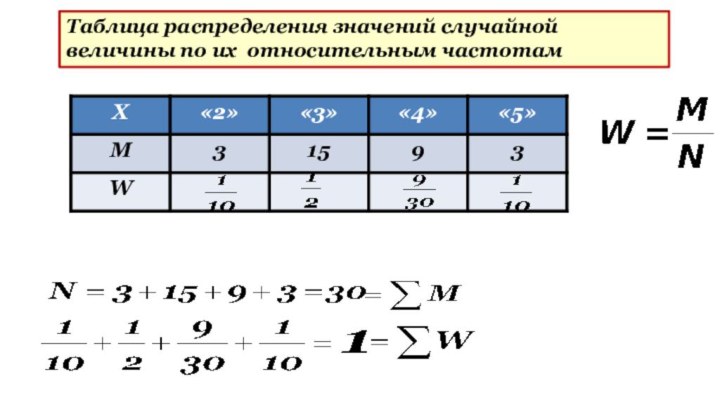
- 9. Таблица распределения значений случайной величины по их относительным частотам
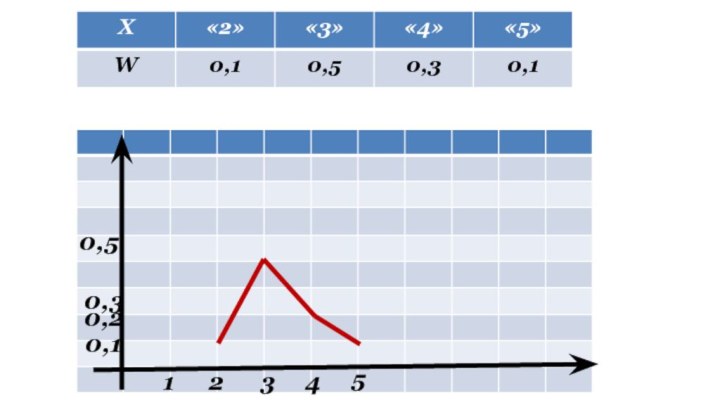
- 10. 0,10,50,30,232145
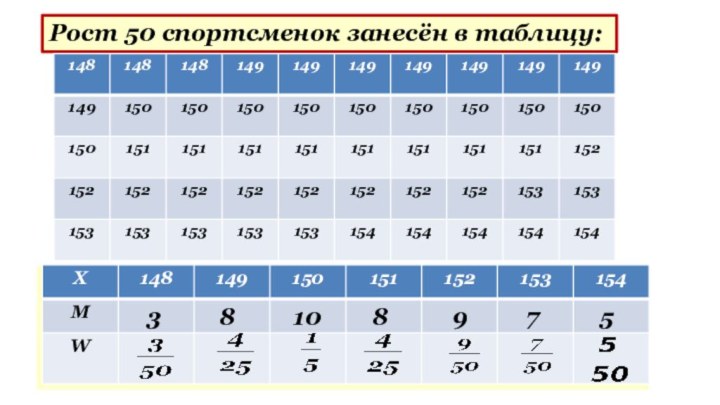
- 11. Рост 50 спортсменок занесён в таблицу:79810835
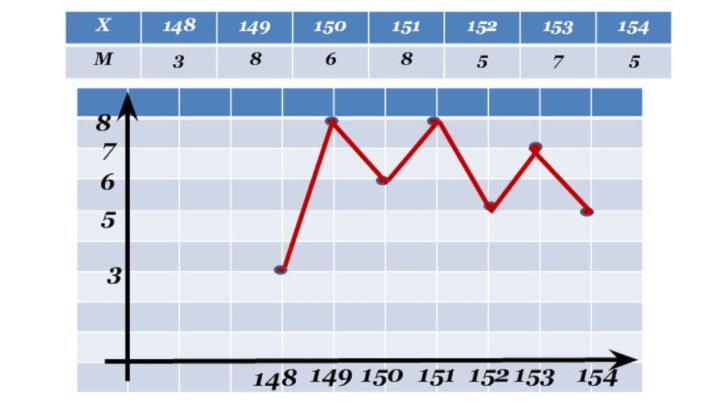
- 12. 85367153154152151150148149
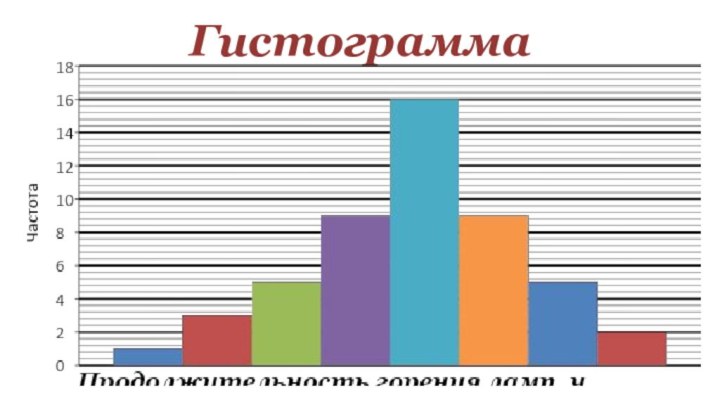
- 13. Гистограммы представляют собой ступенчатую
- 14. Гистограмма
- 15. При изучении реальных явлений часто бывает
- 16. На пример:Генеральная совокупность – жители большого города.
- 17. - объем генеральной совокупности- объем репрезентативной выборки- частоты- частоты в генеральной совокупности
- 18. Для идеально составленной репрезентативной выборки должно выполняться равенство:Где i – порядковый номер значения признака (1≤i≤k).
- 19. Фабрика резиновых изделий выиграла тендер
- 20. N=100 солдат (объем репрезентативной выборки)
- 21. В книгах по статистике моду, медиану и
- 22. Мода23182520252532373426342525Модой ряда чисел называется число, которое встречается в данном ряду чаще других.
- 23. МедианаВ таблице приведены данные о продаже в
- 24. Медиана23182520252532373426342525Составим упорядоченный ряд чисел18; 20; 23; 25;
- 25. Среднее арифметическое: 27 минутСредним значением случайной величиныназывается
- 26. Произвели сбор данных о расходе электроэнергии в
- 27. В городе пять школ. В таблице приведен
- 28. Размах23182520252532373426342537Наибольшее - 18Наименьшее - 37 - 18=
- 29. Меры разбросаОтклонением от среднего называют разность между рассматриваемым
- 30. Меры разбросаОчевидно, отклонение от среднего может быть
- 31. Меры разбросаСреднее арифметическое квадратов отклонений называется дисперсией и обозначается D.
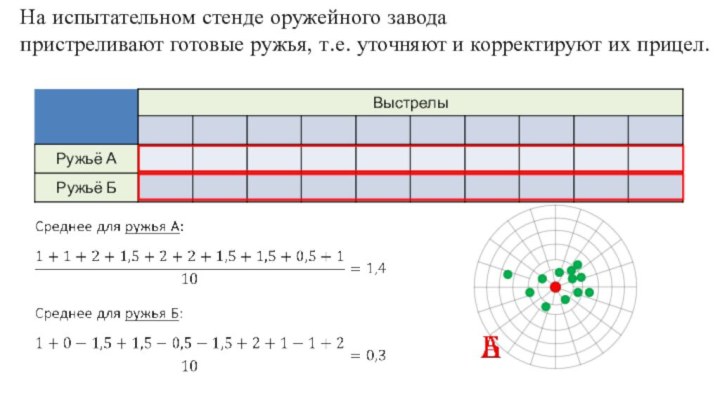
- 32. На испытательном стенде оружейного заводапристреливают готовые ружья, т.е. уточняют и корректируют их прицел.
- 35. Скачать презентацию
- 36. Похожие презентации
Статистика(лат. «status») состояние делСтатистика — это точная наука, изучающая методы сбора, анализа и обработки данных, которые описывают массовые действия, явления и процессы.
Слайд 3
Статистика
(лат. «status») состояние дел
Математическая статистика – это раздел
математики, изучающий методы сбора, систематизации и обработки результатов наблюдений
случайных массовых явлений с целью выявления существующих закономерностей.
Слайд 4
Статистика
(лат. «status») состояние дел
Статистика имеет дело со случайными
величинами.
Случайные величины-величины, которые в ходе наблюдений или испытаний могут
принимать различные значения. Можно сказать, чтоих значения зависят от случая.
Слайд 7
Этапы статистической обработки данных
3. Построить графики
распределения данных
4.
Получить паспорт измерения данных
объём, размах, мода измерения,
среднее (или
среднее арифметическое)1. Упорядочить и
сгруппировать
данные измерения
2. Составить таблицу
распределения данных
Слайд 13 Гистограммы представляют собой ступенчатую фигуру,
составленную из прямоугольников. Основание каждого прямоугольника равно длине интервала,
а высота – частоте или относительной частоте. Таким образом, в гистограмме в отличие от обычной столбчатой диаграммы, основание прямоугольников выбирают не произвольно, а строго определенной длины интервала.Слайд 15 При изучении реальных явлений часто бывает невозможно
обследовать все элементы совокупности.
Вместо изучения всех элементов совокупности,
которую называют генеральной совокупностью, обследуют ее значительную часть, выбранную случайным образом, называемую выборкой. Выборку называют репрезентативной, если в ней присутствуют все значения случайной величины примерно в тех же пропорциях, что и в генеральной совокупности.
Число объектов генеральной совокупности и выборки называют соответственно объемом генеральной совокупности и объемом выборки.
Слайд 16
На пример:
Генеральная совокупность – жители
большого города.
Репрезентативная
выборка – жильцы
многоквартирного дома, в котором
примерно в тех же
пропорциях, что и в самом городе, проживают люди разных
возрастов.
Слайд 17
- объем генеральной совокупности
- объем репрезентативной выборки
- частоты
-
частоты в генеральной совокупности
Слайд 18
Для идеально составленной репрезентативной выборки должно выполняться равенство:
Где
i – порядковый номер значения признака (1≤i≤k).
Слайд 19 Фабрика резиновых изделий выиграла тендер на
изготовление
армейских противогазов. Для определения того, сколько противогазов каждого из пяти существующих размеров следует изготовить, были сделаны замеры у N=100 случайным образом выбранных солдат ближайшей воинской части. Распределение размеров противогазов X по частотам M оказалось следующим:Сколько противогазов каждого размера будет изготавливать фабрика?
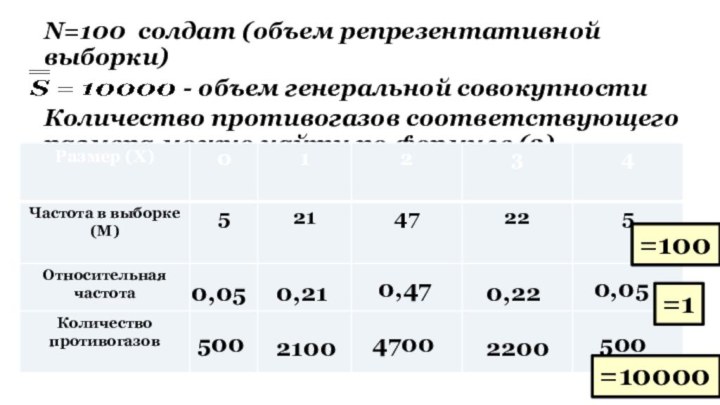
Слайд 20 N=100 солдат (объем репрезентативной выборки)
Количество противогазов соответствующего размера можно найти по формуле (2).
0,05
500
0,21
0,47
0,22
0,05
2100
4700
2200
500
=100
=1
=10000
Слайд 21 В книгах по статистике моду, медиану и среднее
арифметическое объединяют одним термином – меры центральной тенденции
( или, короче, центральные тенденции). Центральные тенденции
Слайд 22
Мода
23
18
25
20
25
25
32
37
34
26
34
25
25
Модой ряда чисел называется
число, которое встречается в
данном ряду чаще других.
Слайд 23
Медиана
В таблице приведены данные о продаже
в течении
недели картофеля, завезённого
в овощную палатку.Найдите медиану ряда чисел.
290
Составим
упорядоченный ряд чисел250; 275; 286; 290; 296; 315; 325
1
2
3
4
5
6
7
Медианой упорядоченного ряда
чисел с нечётным числом членов
называется число,
записанное посередине ряда.
Слайд 24
Медиана
23
18
25
20
25
25
32
37
34
26
34
25
25
Составим упорядоченный ряд чисел
18; 20; 23; 25; 25;
25; 25; 26; 32; 34; 34; 37
Медианой упорядоченного ряда
чиселс чётным числом членов называется
среднее арифметическое двух чисел,
записанных посередине ряда.
Слайд 25
Среднее арифметическое: 27 минут
Средним значением случайной величины
называется среднее
арифметическое всех её значений
При опросе 12 учащихся узнали
время затраченное на выполнение домашнего задания по алгебре. 23; 18; 25; 20; 25; 25; 32; 37; 34; 26; 34; 25
Получили такие данные:
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых.
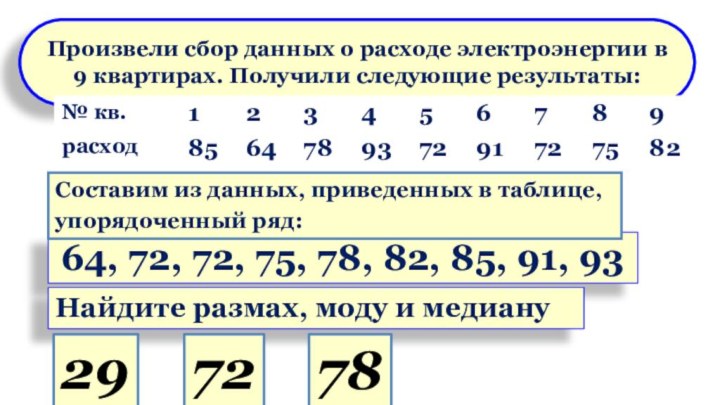
Слайд 26 Произвели сбор данных о расходе электроэнергии в 9
квартирах. Получили следующие результаты:
64, 72, 72, 75, 78, 82,
85, 91, 93Составим из данных, приведенных в таблице,
упорядоченный ряд:
Найдите размах, моду и медиану
29
72
78
Слайд 27 В городе пять школ. В таблице приведен средний
балл, полученный выпускниками каждой из этих школ за экзамен
по математике. Найдите средний балл выпускного экзамена по математике по всему городу?
1. 60+70+30+50+70=280
2. Если умножить количество учеников в школе на средний балл по школе , то получиться сумма баллов в этой школе, а если сложить все такие произведения, то сумма всех баллов по городу равна
60 ∙60+70 ∙54+30 ∙68+50 ∙ 72+70∙54=
=3600+3780+2040+3600+3780 = 16800
3. Средний балл по городу равен 1685400:280=60
Слайд 28
Размах
23
18
25
20
25
25
32
37
34
26
34
25
37
Наибольшее -
18
Наименьшее -
37 - 18
= 19
Меры
разброса
Размахом ряда чисел называется
разность между
наибольшим и наименьшим этих чисел.
Слайд 29
Меры разброса
Отклонением от среднего называют разность между рассматриваемым значением
случайной величины и средним значением выборки.
Пример:
Задана выборка 52,54,50,48,46.
Пусть значение величины X₁=52, а
значение среднего X=(52+54+50+48+46);5=50,
отклонение от среднего X₁−X=52−50=2.
Слайд 30
Меры разброса
Очевидно, отклонение от среднего может быть как
положительным, так и отрицательным числом. Нетрудно понять, что сумма
отклонений всех значений выборки от среднего значения равна нулю. Поэтому характеристикой стабильности элементов совокупности может служить сумма квадратов отклонений от среднего(чем меньше, тем лучше).
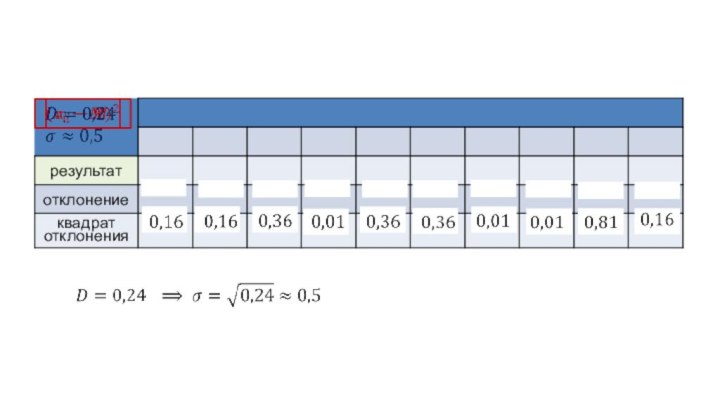
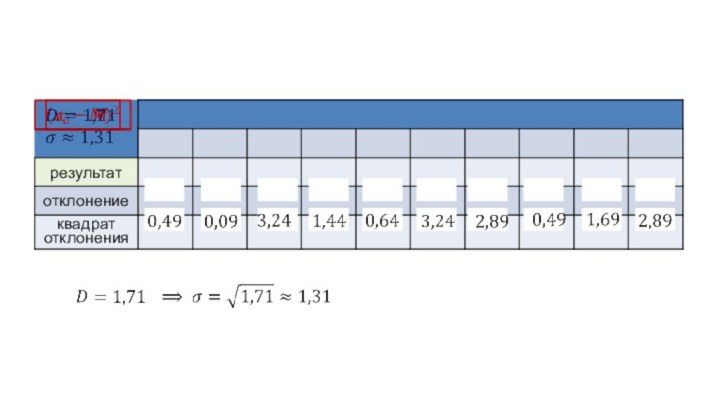
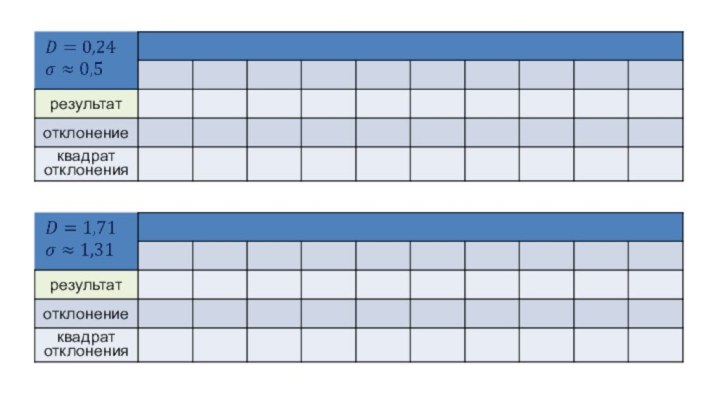
Слайд 31
Меры разброса
Среднее арифметическое квадратов
отклонений называется дисперсией
и обозначается D.
Для оценки
степени отклонения от среднего значения удобно иметь дело с
величиной той же размерности, что и сама величина X. С этой целью используют значения корня квадратного из дисперсииКорень квадратный из дисперсии
называют средним квадратичным
отклонением и обозначают
Слайд 32
На испытательном стенде оружейного завода
пристреливают готовые ружья, т.е.
