Презентация на тему по математике на тему Системы рациональных уравнений (11 класс)

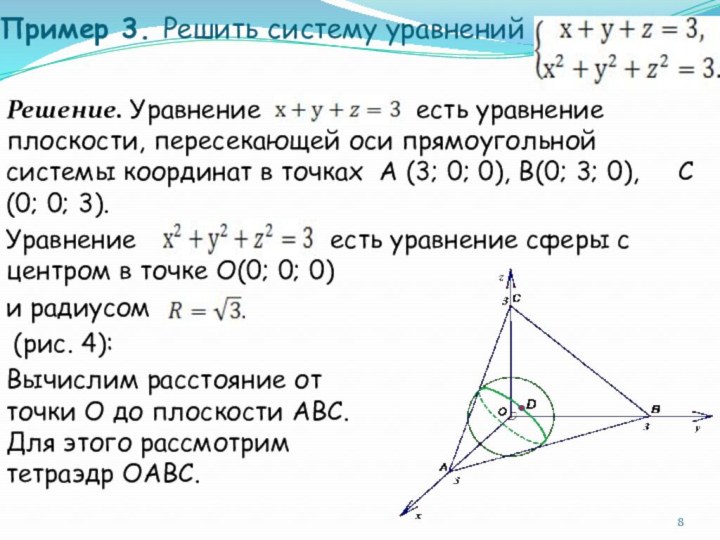
и

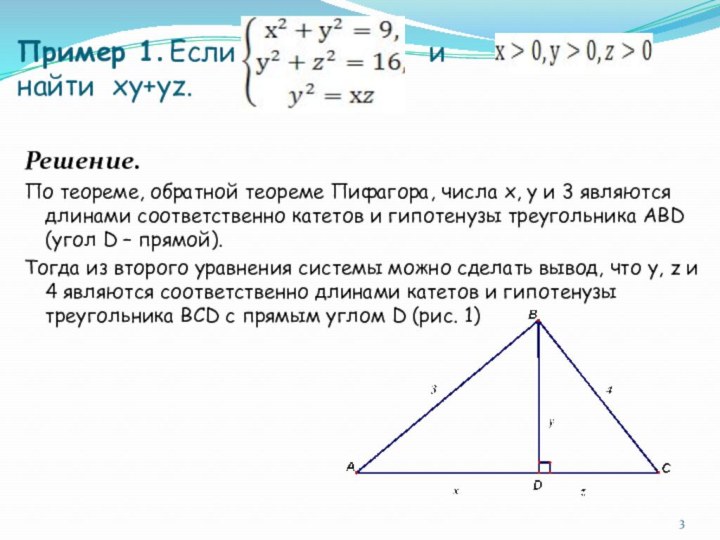
найти ху+уz.

Решение.
По теореме, обратной теореме Пифагора, числа х, у и 3 являются длинами соответственно катетов и гипотенузы треугольника АВD (угол D – прямой).
Тогда из второго уравнения системы можно сделать вывод, что у, z и 4 являются соответственно длинами катетов и гипотенузы треугольника ВСD с прямым углом D (рис. 1)

у есть среднее пропорциональное чисел х и z. Тогда

по теореме, обратной теореме о пропорциональных отрезках в прямоугольном треугольнике, угол АВС – прямой (рис.2).




Рассмотрим выражение ху + уz.

из условий

не находя значений х,у,z, вычислите значение выражения ху+уz+zx.

соответственно катетов и гипотенузы треугольника АОС с прямым углом

АОС,
а числа х, есть длины сторон треугольника АОВ с углом АОВ, равным 1350.
Этот вывод можно сделать, используя теорему, обратную теореме косинусов. Аналогично х, есть длины сторон треугольника ВОС с углом ВОС, равным 1350 (рис.3):

то в △АВС угол АСВ=900.








Тогда искомое

значение ху+уz+zx равно учетверенной площади треугольника АВС.
ху+уz+zx =120.

есть уравнение

плоскости, пересекающей оси прямоугольной системы координат в точках А (3; 0; 0), В(0; 3; 0), С(0; 0; 3).
Уравнение есть уравнение сферы с центром в точке О(0; 0; 0)
и радиусом
(рис. 4):
Вычислим расстояние от точки О до плоскости АВС. Для этого рассмотрим тетраэдр ОАВС.

, где

H=OD (D- центр △АВС), то есть





Объем тетраэдра может быть вычислен иначе:


т.е.

Это означает, что расстояние от точки

О до плоскости АВС равно радиусу сферы, т.е. плоскость касается сферы. Следовательно, точка касания является центром треугольника АВС.
Так как D(х; у; z) – центр равностороннего треугольника АВС, где А(3; 0; 0), В(0; 3; 0), С(0; 0; 3), то х = у= z.
Заменив у и z на х в уравнениях данной системы, получим х=1.

Ответ. (1; 1; 1).

скалярного произведения.

векторов и , уравнение

(2) выражает квадрат длины .
Пусть


Тогда
Подставляя в (1) получаем:
Т.о. х = 1; у = 1; z = 1. Проверим, подставив в (3).
Ответ. (1;1;1).

Пусть



Т.е.

Система имеет бесконечное множество решений.

Пусть




Т.к.

то

и система несовместна.

то х=у=0, z
Если то векторы коллинеарны и, следовательно,
Два значения для с дают две возможности решения системы.

.

.

из второго уравнения системы (1), подставив в неё значения

Например,
Вторая возможность:
Составленные в соответствии с этим условием уравнения

не дают решения исходной системы.