Презентация на тему Квадратичная функция 8-9 классы.

скрытый порядок в хаосе , который нас окружает».

Норберт Винер

(американский учёный, выдающийся математик и философ, основоположник кибернетики и теории искусственного интеллекта).

вас строить замечательную кривую – параболу.
Для этого вам

нужно посмотреть эту презентацию.
Для построения любой параболы вы должны работать по следующему алгоритму:
1. Вычислить координаты вершины параболы.
2. Найти шаги параболы, т.е.
а) коэффициент а при х² это будет первый шаг от вершины вдоль оси ОУ.
б) 2а - это будет второй и последующие шаги вдоль оси ОУ.
И это всё! Очень легко и интересно!

от вершины в следующем порядке:
1 шаг: 1 клетка

вправо, 1 вверх
2 шаг: 1 клетка вправо, 3 вверх
3 шаг: 1 клетка вправо, 5 вверх и т.д.
Аналогично от вершины влево
4 шаг: 1 клетка влево, 1 вверх
5 шаг: 1 клетка влево, 3 вверх
6 шаг: 1 клетка влево, 5 вверх и т.д.

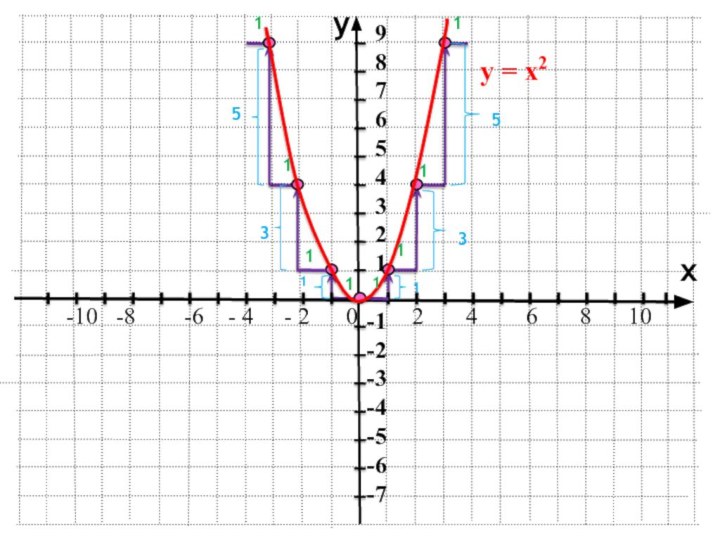
Ребята, все ли вы знаете, что построить любую параболу можно очень просто:
Смотрите как легко!

и с с
Ось
ординат
Координатная плоскость
A(2;3)

- 4 - 2

0 2 4 6 8 10

1

1

1

1

1

1

1

1

3

1

5

1

3

5

у = х2

9
8
7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

-6 -4 -2

0 2 4 6

(0;0)

(1;1)

(2;4)

(3;9)

(-1;1)

(-2;4)

(-3;9)

у = х2

9
8
7
6
5
4
3
2
1

любой параболы.
На факультативе мы изучали метод математической индукции.

Используя этот метод, можно доказать следующее утверждение:
сумма нечётных натуральных чисел равна квадрату количества этих чисел, то есть
1 + 3 + 5 +… + (2k – 1) = n2,
где n – натуральное число.

этих чисел, то есть
1 + 3 + 5 +…

+ (2k – 1) = n2, где n – натуральное число.
Доказательство:
1 + 3 + 5 +… + (2k – 1) = n2.
1) Пусть n =1, тогда 1=1² 2) Пусть n = k, k >1. 1 + 3 + 5 +...+ (2k - 1) = k² - это верно, 3) Докажем данное утверждение при n = k + 1 тогда имеем: 1 + 3 + 5 + ... + (2(k + 1) - 1) = (k + 1)2; 1 + 3 + 5 + ... + (2k - 1) + (2k + 1) = k2 + 2k + 1 = (k + 1)2;

Итак, методом математической индукции мы доказали, что 1 + 3 + 5 + ... + (2k - 1) = n², где n – натуральное число

- 4 - 2

0 2 4 6 8 10

-2

-4

-6

1

1

1

1

1

1

1

1

1,5

0,5

2,5

0,5

1,5

2,5

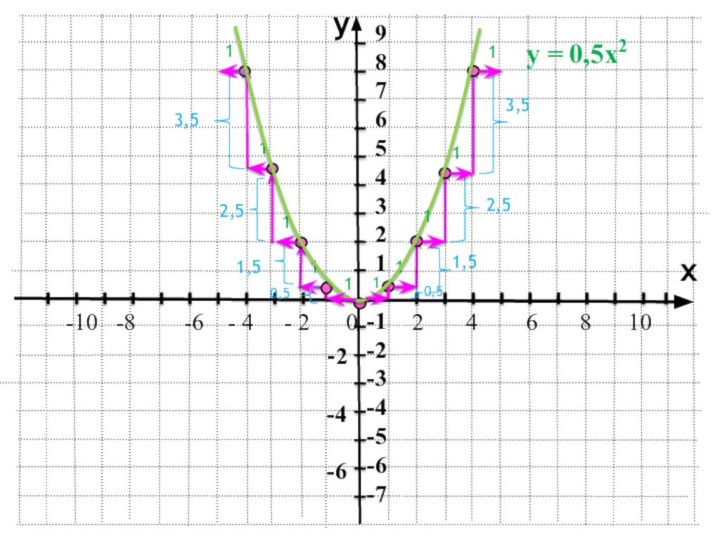
у = 0,5х2

3,5

3,5

1

1

9
8
7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

- 4 - 2

0 2 4 6 8 10

-2

-4

-6

у = 0,5х2

(0;0)

(1;0,5)

(2;2)

(3;4,5)

(4;8)

(-1;0,5)

(-2;2)

(-3;4,5)

(-4;8)

9
8
7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

- 4 - 2

0 2 4 6 8 10

-2

-4

-6

1

1

1

1

1

1

2

6

2

6

у = 2х2

10

10

9
8
7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

- 4 - 2

0 2 4 6 8 10

у = 2х2

(0; 0)

(1; 2)

(-1; 2)

(-2; 8)

(2; 8)

9
8
7
6
5
4
3
2
1

-1
-2
-3
-4
-5
-6
-7

то это не меняет принцип построения.
Координаты вершины принимаем

как (0;0), а построение параболы идёт аналогичным образом,
т. e. построение зависит только от коэффициента перед х2.

параболы находится не в начале координат, и коэффициент

отличен от 1.

4х - 5

4
у = -4х2 +4х - 5
- 8
- 8
1

= -4х2 +4х - 5
(0,5; -4)
(1,5; -8)
(-0,5; -8)

3x -7

- 0,75х2 +3х - 7
- 5,25
- 2,25
- 3,75
-

2,25

- 3,75

- 5,25

1

1

1

1

1

1

+3х - 7
(2;- 4)
(3;- 4,75)
(4; - 7)
(5; - 10,75)
(1;

- 4,75)

(0; - 7)

( - 1; - 10,75)

функции обычной,
Прекрасен в простоте своей!