Слайд 2
В столярке работает четверо нас:
Беляев, Гуляев, Анютка, Тарас.
Вот
как-то профорг заглянул на минутку:
- Кто ходит на лыжах?
-
Тарас и Анютка.
- Кто плавать умеет?
- Анютка, Тарас.
- Кто в теннис играет?
- Они же, как раз.
- Есть шахматисты?
- Беляев, Гуляев.
- Мотоциклисты?
- Беляев, Гуляев.
- Бывал ли в походе кто-либо из вас?
- Беляев, Гуляев, Анютка, Тарас.
Устроили наши ответы профорга,
Он все записал, не скрывая восторга.
А вскоре весьма и весьма озадачены,
Читали в стенновке мы рапорт такой:
«Пятнадцатью видами спорта охвачены
Все сорок рабочих у нас в мастерской!»
стихи С. Погорельского
Слайд 3
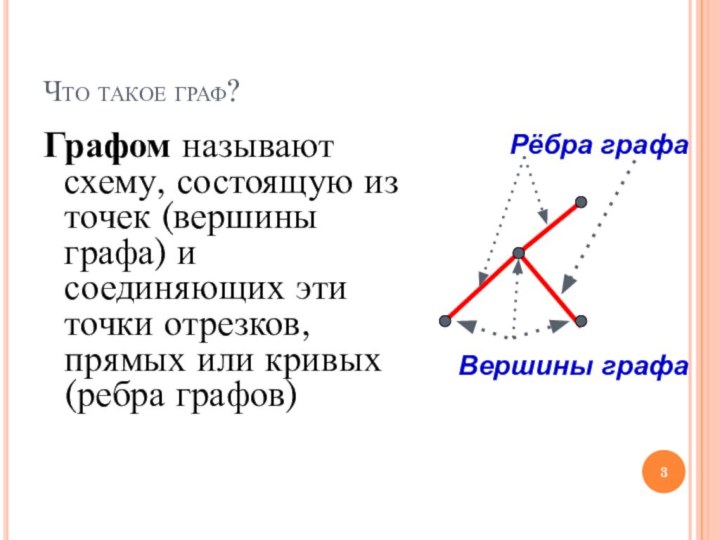
Что такое граф?
Графом называют схему, состоящую из точек
(вершины графа) и соединяющих эти точки отрезков, прямых или
кривых (ребра графов)
Рёбра графа
Вершины графа
Слайд 4
2 вершины и
1 ребро
3 вершины и
3 ребра
4 вершины и
5 ребер
6 вершин и
6 ребер
Слайд 5
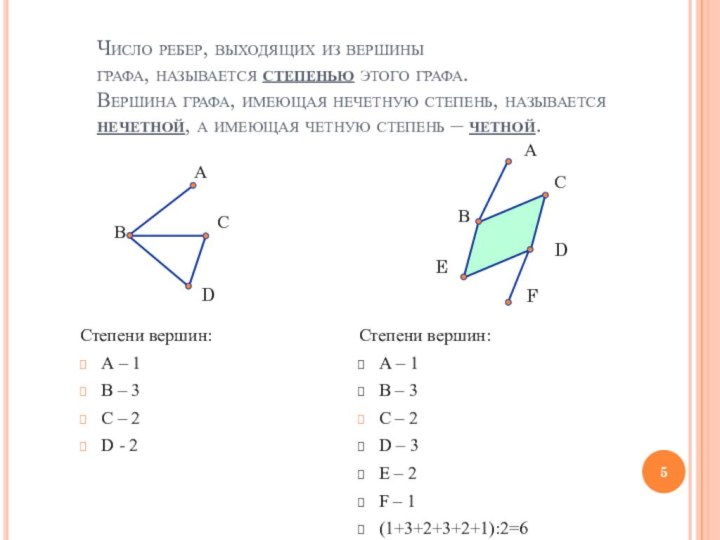
Число ребер, выходящих из вершины
графа, называется степенью
этого графа.
Вершина графа, имеющая нечетную степень, называется нечетной, а
имеющая четную степень – четной.
Степени вершин:
А – 1
В – 3
С – 2
D - 2
Степени вершин:
А – 1
В – 3
С – 2
D – 3
E – 2
F – 1
(1+3+2+3+2+1):2=6
Слайд 6
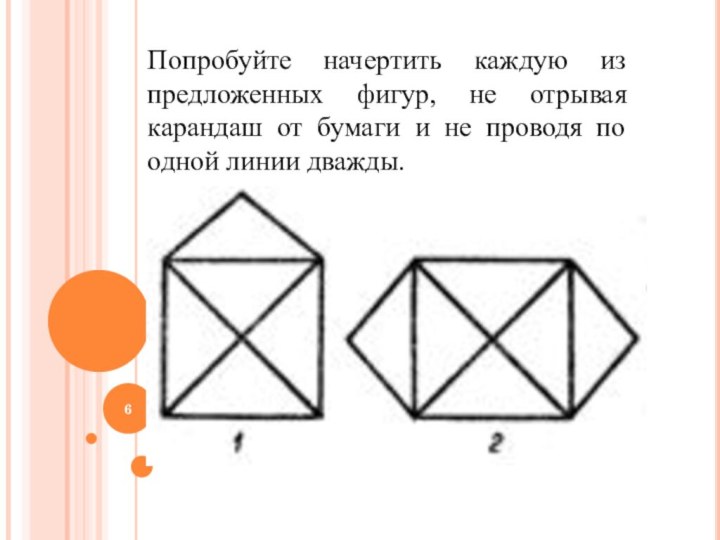
Попробуйте начертить каждую из предложенных фигур, не отрывая
карандаш от бумаги и не проводя по одной линии
дважды.
Слайд 7
Какие буквы русского алфавита можно нарисовать одним росчерком?
Б,
В, Г, З, И, Л, М, О, П, Р,
С, Ф, Ъ, Ь, Я.
Слайд 8
Задача о Кенигсбергских мостах
Бывший Кенигсберг (ныне Калининград) расположен
на реке Прегель. В пределах города река омывает два
острова. С берегов на острова были перекинуты мосты. Старые мосты не сохранились, но осталась карта города, где они изображены.
Слайд 9
Задача о Кенигсбергских мостах
Кенигсбергцы предлагали приезжим следующую задачу:
пройти по всем мостам и вернуться в начальный пункт,
причём на каждом мосту следовало побывать только один раз.
Слайд 10
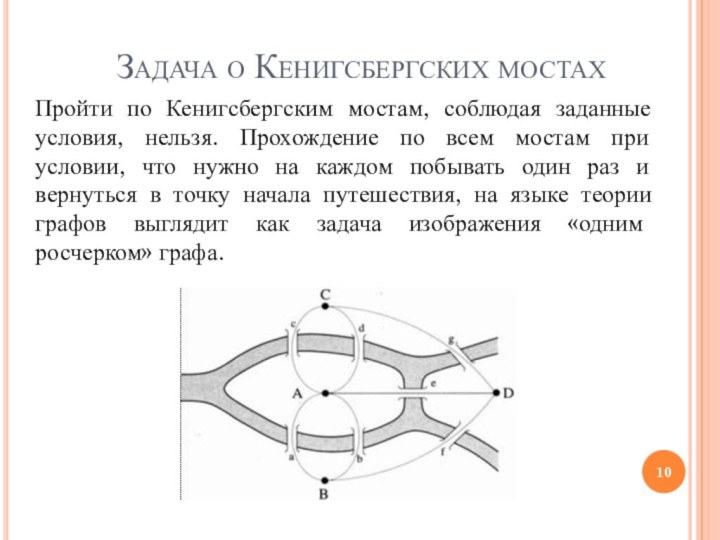
Задача о Кенигсбергских мостах
Пройти по Кенигсбергским мостам, соблюдая
заданные условия, нельзя. Прохождение по всем мостам при условии,
что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа.
Слайд 11
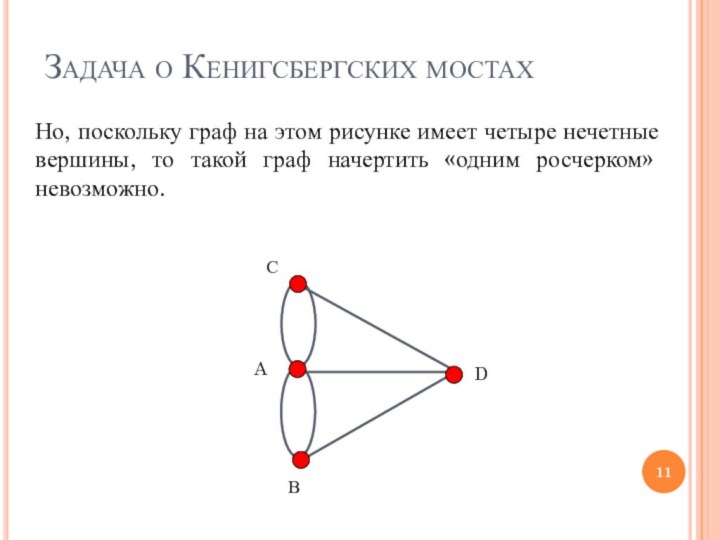
Задача о Кенигсбергских мостах
Но, поскольку граф на этом
рисунке имеет четыре нечетные вершины, то такой граф начертить
«одним росчерком» невозможно.
С
В
D
A
Слайд 12
Одним росчерком
Граф, который можно нарисовать, не отрывая карандаша
от бумаги, называется эйлеровым.
Решая задачу О кенигсбергских мостах,
Эйлер сформулировал свойства графа:
Невозможно начертить граф с нечетным числом нечетных вершин.
Слайд 13
Художник-авангардист нарисовал картину "Контур квадрата и его диагонали".
Мог ли он нарисовать свою картину не отрывая карандаша
от бумаги и не проводя одну линию дважды?
Слайд 14
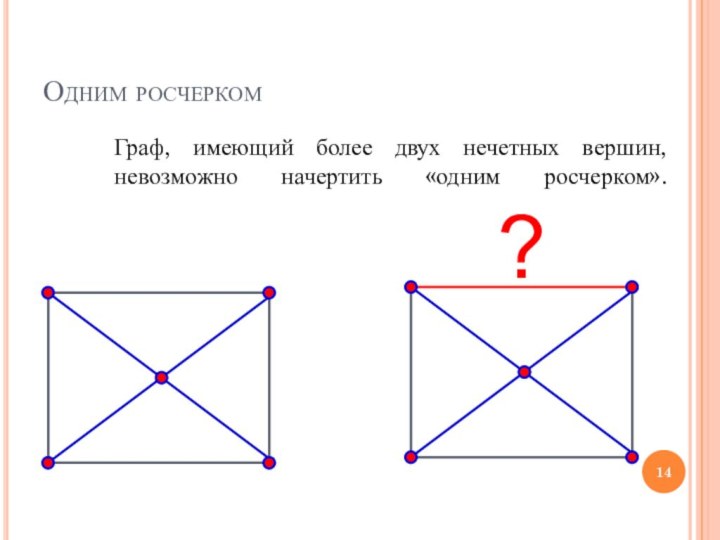
Одним росчерком
Граф, имеющий более двух нечетных вершин, невозможно
начертить «одним росчерком».
?
Слайд 15
Можно ли нарисовать эту картинку, не отрывая карандаша
от бумаги и проходя по каждой линии по одному
разу?
Слайд 16
Задачи
Алеша, Боря и Витя учатся в одном классе.
Один ездит домой из школы на автобусе, другой –
на трамвае, третий – на троллейбусе. Однажды после уроков Алеша пошел проводить друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадь!» Кто на чем ездит домой?
Слайд 17
В компании из семи мальчиков каждый имеет среди
остальных не менее трёх братьев. Докажите, что все семеро
– братья.
Слайд 18
Между 9 планетами Солнечной системы введено космическое сообщение.
Ракеты летают по следующим маршрутам: Земля-Меркурий, Плутон-Венера, Земля-Плутон, Плутон-Меркурий,
Меркурий-Венера, Уран-Нептун, Нептун-Сатурн, Сатурн-Юпитер, Юпитер-Марс и Марс-Уран. Можно ли добраться с Земли до Марса?
Слайд 19
«Если задуманное число умножить на 5 и к
полученному результату прибавить 1, потом полученную сумму умножить на
7 и полученное произведение увеличить на 4, то получим число, которое в 16 раз больше числа 135. Найдите задуманное число».
Слайд 21
Машина ехала 3 часа со скоростью 65 км/ч
и 2 часа со скоростью 60 км/ч.
Какой путь
она пройдет за эти 5 часов?
S1
160 км
t 1= 2 ч
S 2
185 км
v 2
t 2= 5 ч
v1
S общ
315 км
Слайд 23
С помощью графов указываются различные связи между
объектами.
Слайд 24
Инженер чертит схемы электрических цепей.
Химик рисует структурные формулы,
чтобы показать, как в сложной молекуле с помощью валентных
связей соединяются друг с другом атомы.
Историк прослеживает родословные связи по генеалогическому дереву.
Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление.
Социолог по сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпораций.
Слайд 26
Изучение графов позволяет:
Развивать интерес к предмету математика.
Сформировать представление
о значении теории графов как средства описания действительности
Развивать логическое
мышление, умение анализировать при решении задач.
Применять элементы теории графов в других предметах.