- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок. Презентация по математике на тему Решение систем линейных уравнений (7 класс)
Содержание
- 2. Эпиграф:«Мне приходится распределять свое время между политикой и уравнениями. Но уравнения, полагаю, намного важнее».
- 3. Актуализация
- 4. - физик-теоретик, один из основателей современной теорети-ческой физики, лауреат Нобелевской премии по физике 1921 года. Альберт Эйнштейн
- 5. Нас в повседневной жизни окружают системы.Линейные системы уравнений
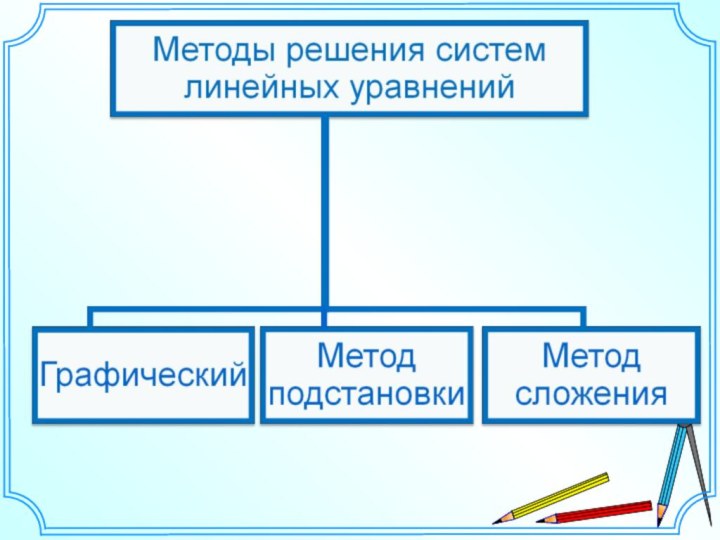
- 6. 1.Какую математическую модель называют системой уравнений с
- 8. Историческая справкаВсе эти методы решения систем уравнений
- 9. A(0;3)B(3;0)C(0;-3)D(3;3)M(2;1)X=2Y=1Ответ: (2;1)Графический метод.х+у=3-2х+у=-3У=-Х+3У=2Х-3. 1.Выразить переменную у из
- 10. 2. Решить систему графическим методом2x +
- 11. Метод подстановкиу - 2х=4,7х - у =1;у=2х+4,7х
- 12. 3. Решить систему методом подстановки2x + y
- 13. |·( -3)+- 4х = - 12,
- 14. 4.Решить систему уравнений методом сложения (вычитания) x
- 15. МИНУТКА отдыха
- 18. Решить систему линейных уравнений: 1.
- 19. 1.Зависит решение системы от метода решения?
- 20. Сколько решений имеет система уравнений ?
- 21. Заполни таблицу:НаглядностьНеточностьТочныйТрудоёмкие выкладки Выбор множителяТочный
- 22. Верно ли?1. Решение системы линейных уравнений
- 23. Тест
- 24. СправкаУравнения с несколькими переменными, для которых требуется
- 25. Итоги. Какие выводы мы можем сделать по
- 26. Рефлексия
- 27. «Зачем мне тратить столько времени на какие-то
- 28. Домашнее задание 14.8, 13.18, 13.13 п.11-13
- 29. Скачать презентацию
- 30. Похожие презентации
























Слайд 2
Эпиграф:
«Мне приходится распределять свое время между политикой и
уравнениями. Но уравнения, полагаю, намного важнее».
Слайд 3 Актуализация
1.
Задание1. Какое из уравнений является линейным уравнением с двумя переменными?
П) 6ху=11 Э) 3х-2у=7 Р) 5х2+у2=8
2. Какая пара чисел является решением уравнения 4х-у=1?
Й) (2;7) А) (5;0) Е) (-3;4)
3. В уравнении 3х+у=18 выразите у через х:
К) у=18+3х Л) х=18-у Н) у=18-3х
4. График какого из уравнений параллельный оси Ох?
Ш) у=10 щ) х=-2 Р) х+у=0
5. Точка с абсциссой 3 принадлежит графику уравнения 2х+у=4. Определите ординату этой точки.
К) 6 Т) -2 Н) 4
6. Точка с ординатой 2 принадлежит графику уравнения 2х+у=4. Определите абсциссу этой точки.
Е) 1 О) 0 И) 4
7. Какие из точек лежат на оси Оу?
А) (3;0) Й) (0;-2) О) (1;1)
8. На каком из рисунков изображен график функции х+у=4?
Н) Р) К)
Слайд 4
- физик-теоретик, один из основателей современной теорети-
ческой физики,
лауреат Нобелевской премии по физике 1921 года.
Альберт Эйнштейн
Слайд 6
1.Какую математическую модель называют системой уравнений с двумя
переменными?
2. Что называют решением системы двух линейных уравнений с
двумя переменными? 3. Что значит решить систему уравнений?
4. Какие методы решения систем уравнений знаете?
Система уравнений – это два и более уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Решить систему уравнений - значит найти все её решения или доказать ,что решений нет
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Слайд 8
Историческая справка
Все эти методы решения систем уравнений знали
люди давно.Они имеются в книге Ньютона “Всеобщая арифметика”, которая
была издана в 1707 году.
Слайд 9
A(0;3)
B(3;0)
C(0;-3)
D(3;3)
M(2;1)
X=2
Y=1
Ответ: (2;1)
Графический метод.
х+у=3
-2х+у=-3
У=-Х+3
У=2Х-3
.
1.Выразить переменную у из каждого
уравнения системы
2. Построить графики полученных функций
3. Найти точки
пересечения графиков
Слайд 10
2. Решить систему графическим методом
2x + y
= 5,
4x + 2y = 6
2x + y =
5, 2x + y = 3
у=5-2х
у= 3-2х
Слайд 11
Метод подстановки
у - 2х=4,
7х - у =1;
у=2х+4,
7х –
(2х+4)=1;
7х - 2х - 4 = 1;
5х = 5;
х=1;
Ответ:
(1; 6)Решим уравнение
Подставим
Выразим у через х
Подставим
Подставим
Слайд 12
3. Решить систему методом подстановки
2x + y =
2,
6x – 2y = 4
3х-2+2х=2
5х=4
х =
0,8 у = 0,4 2x + y = 2,
3x – y = 2
у =2-2х
3х-у =2
Слайд 13
|·( -3)
+
- 4х = - 12,
х=3;
Ответ: (3; - 10)
1. Если требуется уравнять коэффициенты при
одной из неизвестных переменных в обоих уравнениях.2. Складываем или вычитаем полученные уравнения
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
Метод сложения
Слайд 14
4.Решить систему уравнений
методом сложения (вычитания)
x -2 y
= 10,
4x – 8y = 40
x - 2y
= 10 (4) 4х-8у=40, 4 х - 8у =40 4х - 8у=40
Слайд 18
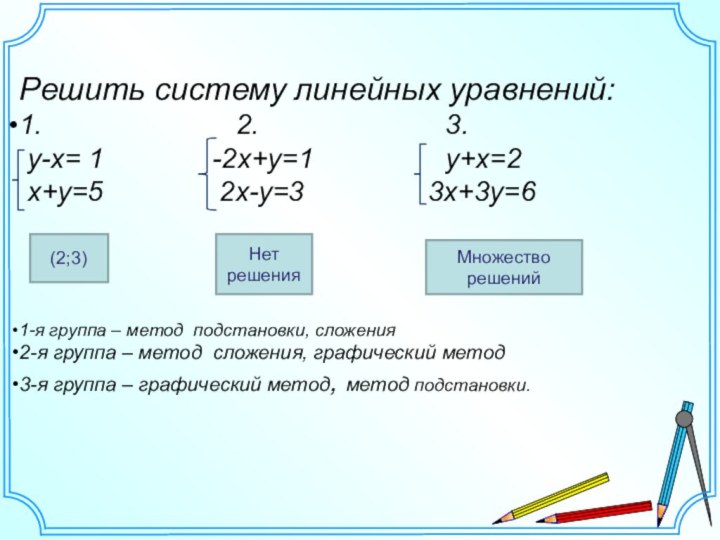
Решить систему линейных уравнений:
1.
2. 3.
y-x= 1 -2х+у=1 y+x=2
x+y=5 2х-у=3 3x+3y=6
1-я группа – метод подстановки, сложения
2-я группа – метод сложения, графический метод
3-я группа – графический метод, метод подстановки.
(2;3)
Нет решения
Множество решений
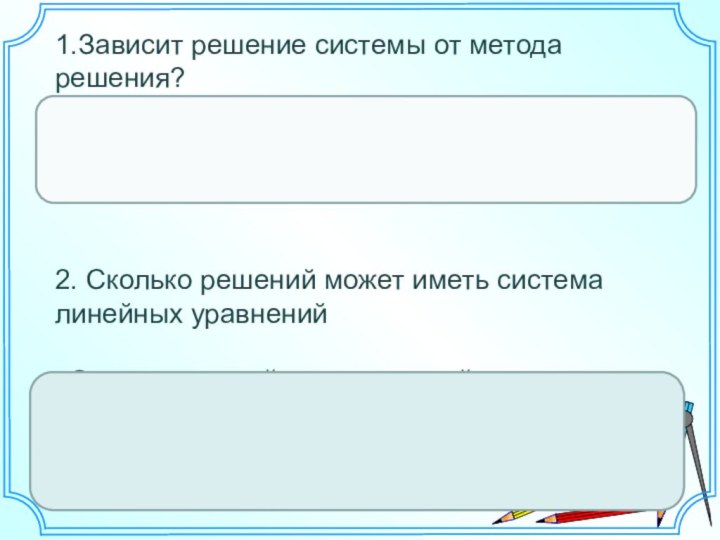
Слайд 19 1.Зависит решение системы от метода решения?
Решение системы не зависит от метода решения.
2. Сколько
решений может иметь система линейных уравненийСистема линейных уравнений может иметь одно решение, бесконечно много решений или вообще не иметь решений.
Слайд 22
Верно ли?
1. Решение системы линейных уравнений зависит
от метода решения. 2. Система линейных уравнений может иметь бесконечно
много решений. 3. Системы линейных уравнений могут иметь два решения. 4. Пара чисел (6; 1) является решением системы уравненийх – у = 5
х + у =7
5.Система линейных уравнений имеет одно решение.
5х-у=4
5х –у=10
нет
нет
нет
да
да
Слайд 24
Справка
Уравнения с несколькими переменными, для которых требуется найти
решения в натуральных или целых числах, называют диофантовыми уравнениями.
Придумал Диофант и два основных приема решения уравнений:– перенос неизвестных; – приведение подобных.
Слайд 25
Итоги.
Какие выводы мы можем сделать по методам
решения систем уравнений?
- Решение системы не зависит от метода
решения.- Система линейных уравнений может иметь одно решение, бесконечно много решений или вообще не иметь решений.
Слайд 27 «Зачем мне тратить столько времени на какие-то уравнения,
если мне это в будущем не понадобится?»
В быту
это вряд ли пригодится. Решение задачи о месте и времени встречи промыслового рыболовецкого судна с перегрузчиком сводится по сути к решению систем линейных уравнений, использующих данные о координатах судов, их скоростях и метеоусловия.





























