Презентация на тему Решение тригонометрических уравнений на интервале.

Математический диктант
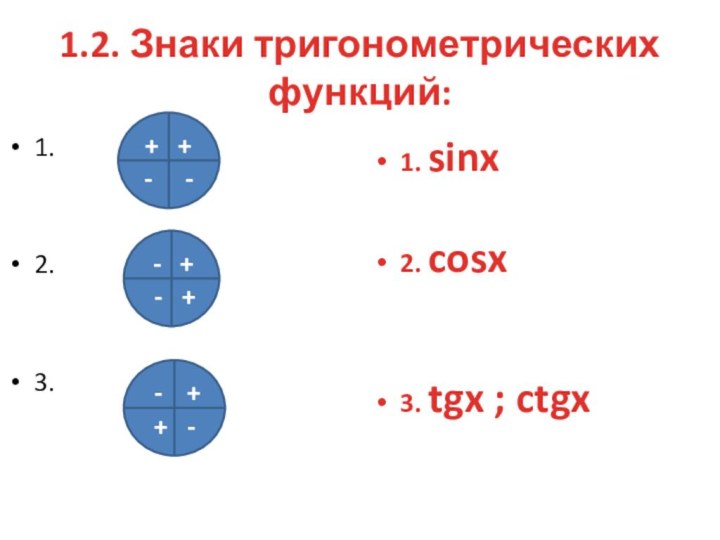
1.2 Знаки тригонометрических функций

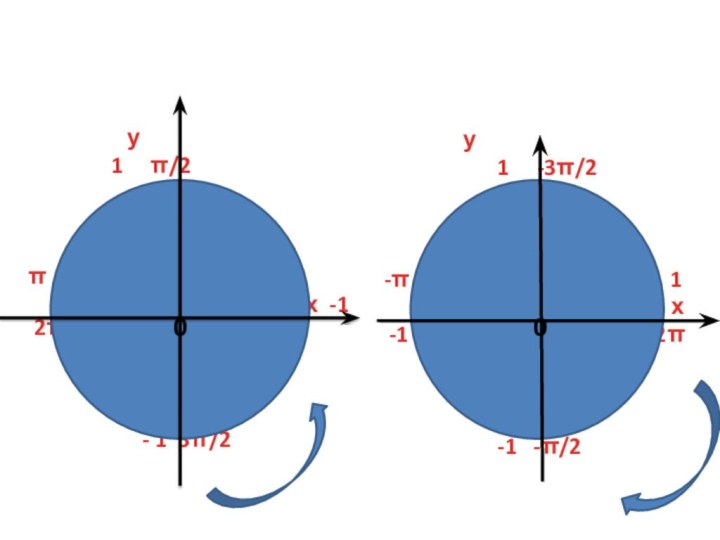
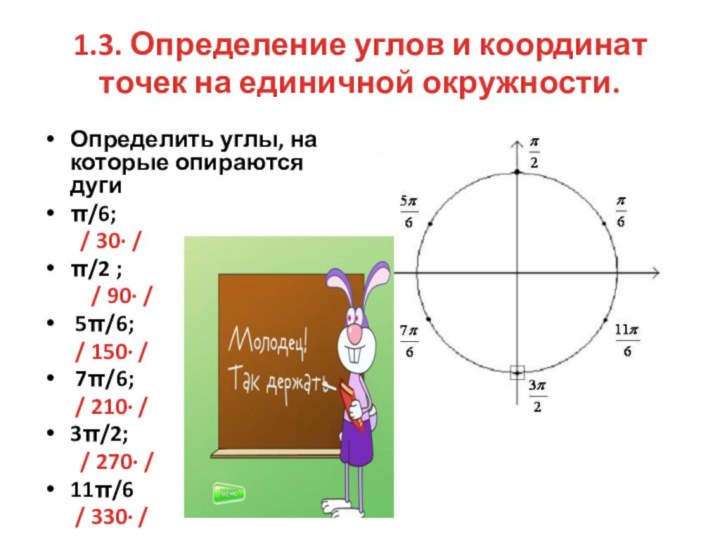
1.3 Определение углов и координат точек на единичной окружности.
1.4 Формулы приведения.
2. Новый материал
2.1 Вспомним некоторые факты из жизни уравнений.
2.2 Алгоритм решения тригонометрических уравнений на интервале.
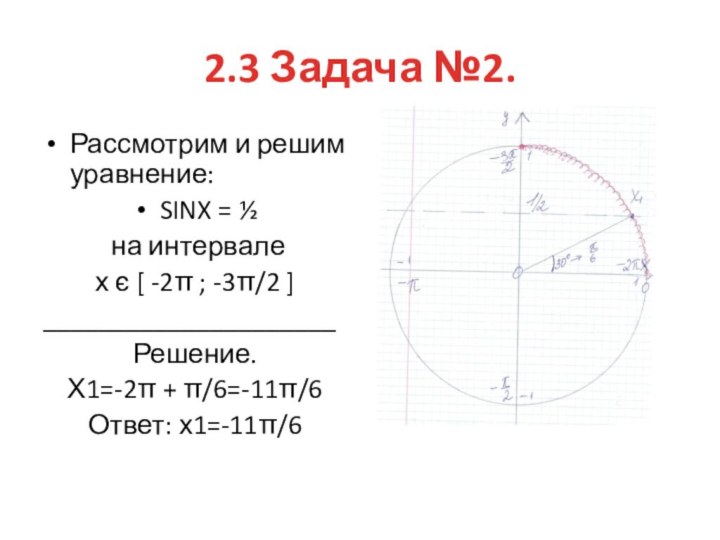
2.3 Разбор задачи.
2.4 Подсчитаем: извлечение корня.
2.5 Решение задач у доски.
2.6 Самостоятельная работа.
3. Домашнее задание
4. Подведение итогов.

тригонометрических функций;
уметь применять формулы приведения при решении уравнений;
уметь

использовать основные формулы тригонометрии при приведении тригонометрических уравнений к простейшему виду;
уметь формировать и находить интервал с положительными и отрицательными числами;
уметь находить табличные данные для тригонометрических функций;
Должны уметь решать уравнения на интервале;

3. Cosx –


4. Sin(-x) –
5. Cos(-x) –

6. Tg(-x) –
7. Ctg(-x) -

1. Наука, изучающая измерение углов в треугольнике.
2. ордината точки, лежащей на единичной окружности.
3. абсцисса точки, лежащей на единичной окружности.

4. - Sinx
5. Cosx
6. – Tgx
7. - Ctgx

; ctgx
+ +
- -
-

+
- +

- +
+ -

у
1 π/2



π 1
х -1 2π



- 1 3π/2

у
1 -3π/2



-π 1
х
-1 -2π



-1 -π/2

0

0

окружности.
Определить углы, на которые опираются дуги
π/6;

/ 30· /
π/2 ;
/ 90· /
5π/6;
/ 150· /
7π/6;
/ 210· /
3π/2;
/ 270· /
11π/6
/ 330· /

в тригонометрических функциях?
3. Наши исключения:
Sinx=1
Sinx=-1
Sinx=0
Cosx=0
Cosx=1
Cosx=-1
1. Выражение со знаком равенства,

содержащее одно или несколько неизвестных, которые требуется найти.
2. Это аргумент, который мы и будем искать!

3. решением является:
Х=π/2 + 2πn, nєZ
Х=3π/2 + 2πn или х=- π/2 + 2πn, nєZ
Х=πn, nєZ
X=π/2 + πn, nєZ
X=2πn, nєZ
X=π + 2πn, nєZ

интервале
х є [ π/2 ; 2π ]
2.2 Алгоритм

решения:
1. изобразим на единичной окружности данный интервал.
-----------------------------------------
2. упростим, если требуется, уравнение, т.е. приведем его к простейшему виду: sinx=a или cosx=a.
-----------------------------------------------
3. отметим значение функции на координатных осях; sinx – на оси «y» или cosx – на оси «x».
---------------------------------------------
4. проведем пунктиром линию до пересечения с окружностью.
-----------------------------------------
5. отметим те точки окружности, которые попали в интервал.
-----------------------------------------
6. вычислим значения этих точек.
--------------------------------------------
7. оформим ответ.

условию интервал.
2. уравнение уже приведено к виду sinx =

a.
3.Отмечаем на оси оу значение ½.
4. проводим пунктиром линию до пересечения с окружностью через точку у=1/2.
5. Видим, что в данный интервал попало только одно значение х1.
6. Производим расчет х1:
Х1 = π – π/6 = 5π/6.
Точка х2 = π/6 не принадлежит интервалу [π/2; 2π], это посторонний корень
7. Ответ: х1 = 5π/6

на интервале
х є [ -2π ; -3π/2 ]
_____________________
Решение.
Х1=-2π

+ π/6=-11π/6
Ответ: х1=-11π/6

Решить уравнение

Cos²x=0,5
на интервале [3π/2; 5π/2 ]

sin²x=0,75
на интервале [-2π; -π/2 ]
_____________________
Решение:
Х1=-2π+π/3=-5π/3
Х2=-π-π/3=-4π/3
Х3=-π+π/3=-2π/3
_________________________

балов

Менее 17 балов
Оценка «5».


Оценка «4».

Оценка «3».