Презентация на тему к научно-исследовательской работе Его величество процент

вычислений.
Задачи:
изучить научную литературу по теме исследования;
рассмотреть основные классы

задач на проценты;
показать применение понятия процента при решении реальных задач из разных сфер жизнедеятельности человека;
познакомится с формулой сложных процентов;
обобщить результаты работы

часто встречается в повседневной жизни.
Любой человек должен уметь

свободно решать задачи, предлагаемые самой жизнью, уметь просчитывать различные предложения магазинов, кредитных отделов и различных банков и выбирать наиболее выгодные.

то же время это одна из сложных тем школьного

курса математики

Предмет исследования: Проценты Объект исследования: Проценты в школе и современной жизни человека

В 1685 году в Париже была издана книга

«Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход.
После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.
Изобретение математических знаков и символов значительно облегчило изучение математики и способствовало дальнейшему ее развитию.

Появление и обозначение процента

что буквально означает «за сотню» или
«со ста». Проценты

дают возможность легко сравнивать между собой части целого, упрощая расчёты.
Пример: Что больше ½ или ¾?

Для чего и когда появился процент?

½ = 50 % < ¾ = 75 %

История процентов
И первыми идею

выражать таким образом части целого в одних и тех же долях, придумали древние вавилоняне. Дело в том, что этот строй пользовался шестидесятеричными дробями, поэтому им просто необходимо было такое нововведение. До наших дней дошли клинописные таблицы вавилонян, при помощи которых можно легко и быстро определить, какова сумма процентных денег. Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы.

убыток на каждые сто рублей. Они применялись только в

торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, в экономических расчетах, в страховании, статистике, науке и технике.

В процентах выражаются ставки налогов, доходность капиталовложений, плата за заемные денежные средства (например, кредиты банка), темпы роста экономики и многое другое.

Римляне брали с должника лихву (т. е. деньги сверх того, что дали в долг). При этом говорили: «На каждые 100 сестерциев долга заплатить 16 сестерциев лихвы».

доля целого (принимаемого за единицу) или сотая часть единицы.

Используется для обозначения доли чего-либо по отношению к целому.

Запись 1% означает 0,01 или 1/100.


Так как 1 % равен сотой части величины, то вся величина равна 100%

Знакомство с процентом.

в процентах, то можно в этой дроби перенести запятую

на два знака вправо и к полученному числу приписать знак %. Справедливо и обратное правило.

0,07 % = 0,0007; 0,451 = 45,1 %;
100 % = 1; 2 = 200 %.

Чтобы выразить в процентах часть величины, заданную обыкновенной дробью, нужно сначала эту дробь обратить в десятичную.

3/8 = 0,375, т. е. 3/8 – это 37,5 %

по 5 кг каждая, то есть 85 кг. Справедливо

также утверждение, что 200 % от 500 кг является 1000 кг. Поскольку по отношению к половине тонны, тонна соответствует 2×100 %.

по существу, являются теми же задачами на дроби.

1. Нахождение

процента от числа
Чтобы найти указанное число процентов от данного числа, нужно проценты записать дробью, а затем данное число умножить на эту дробь.
Пример. Швейная фабрика выпустила 1200 костюмов. Из них 30% - костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

1200 ∙30/100 = 1200 ∙0,3 = 360 костюмов нового фасона выпустила фабрика.

Виды задач на проценты с примерами.

число по его проценту, нужно проценты записать дробью, а

затем данное число соответствующее проценту разделить на эту дробь.
Пример. За тест по математике отметку «5» получили 12 учеников, что составляет 30% всех учеников. Сколько учеников выполняло тест?
12 : 0,3 = 40 учеников выполняло тест
3. Сколько процентов составляет одно число от другого
Чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.
Пример. Завод произвёл за год 40000 автомобилей, а в следующем году –  только 36000 автомобилей. Сколько процентов это составило по отношению к выпуску предыдущего года?
36000 : 40000 100 = 90% .

изготовил 720 деталей за смену, перевыполнив план на 20

%. Сколько деталей составляет плановое задание рабочего?
720/(1+20/100) = 720/(1+1/5) = 720/1,2 = 600

Пример. Денежная сумма к выдаче за минусом подоходного налога (13 процентов). Пусть оклад составляет 10 000 рублей. Тогда сумма к выдаче составляет:
10000 * (1 - 13 / 100) = 10000 * 0.87 = 8700.

Число учащихся, записавшихся в данную школу, выросло с 351

до 396 человек. На сколько процентов возросло это число?

Прирост составил 396 – 351 = 45 человек. Записывая дробь 45/351 в процентах, получаем:    
 
45/351 = 0,128 = 12,8%.

была 200 рублей. В феврале его стоимость подорожала на

15%, а в марте – ещё на 20%. Какая стала стоимость билета в цирк в марте.

Немного житейских задач.

феврале, т.е. найдём 15% от 200 р. 15% от

стоимости билета – это 0,15 рублей: 200 0,15=30 (р.). Теперь можно определить стоимость билета в феврале:
200+30=230 (р.).
Чтобы узнать мартовскую стоимость билета, нужно найти 20% от февральской стоимость билета и прибавить полученное число к 230:
20% от стоимости билета – это 0,2 рублей: 230 0,2=46 (р.).
230+46=276 (р.).

Решение задачи 1

с папой решили купить ему новый компьютер. Первоначальная стоимость

компьютера составляла 20 000 руб. Семье повезло дважды: воскресная скидка 5 % и новогоднее предложение – скидка 10 %. Определите цену товара после двух понижений: сначала на 5 %, а потом на 10 %.

%;
20 000 – 1000 = 19 000 руб. –

цена после первой скидки;
19 000/10 = 1900 руб. – составляют 10 %
19 000 – 1900 = 17 100 руб. – цена товара после двух понижений.

Решение задачи 2

вы­су­шен­ные — 28%. Сколь­ко сухих фрук­тов по­лу­чит­ся из 288

кг све­жих фрук­тов?

в экономике о которых настойчиво сообщают нам все средства

массовой информации. Для этого они были придуманы много лет тому назад – это проценты в сфере бизнеса.

реальной жизни, и наиболее удачной оказалась задача на расчет

кредитов. С математической точки зрения она интересна тем, что не входит в школьную программу. Действительно, в наше время люди все чаще и чаще берут товары в кредит (ссуда в денежной или товарной форме, предоставляемая кредитором заемщику на условиях возвратности, чаще всего с выплатой процента за пользование ссудой), который доступен каждому.
Конечно же, всем хочется приобрести нужный товар, как можно выгодней. В нашем селе банков нет. Для проведения этого эксперимента я решила рассмотреть различные формы кредитов и вкладов в двух банках нашего района: «Сбербанка» и «РоссельхозБанка». Для этого не обойтись без формулы сложных процентов.

Sn=S0 (1+0,01 р)n ( n – срок кредита).

Опытно-экспериментальная работа

без обеспечения в РоссельхозБанке и Сбербанке. Такой кредит оптимален

в случае, если Вам нужна незначительная сумма денежных средств, а также для Вас важно максимально простое оформление кредита. Важной особенностью такого кредита является то, что он осуществляется на любые цели без залога и поручительства.

Допустим, мы решили взять кредит на 450 000 рублей сроком на 5лет. По формуле сложных процентов Sn=S0 (1+0,01 р)n найдем сумму денежных средств, причитающихся к возврату по окончании срока кредита:

выплат в каждом банке.

Вывод: Стоимость кредита в
РоссельхозБанке составит

600 600 рублей, а в Сбербанке
599 200 рублей , т.е разница
стоимости кредита в двух банках =
1400 рублей. Таким образом,
выгоднее брать потребительский
кредит в Сбербанке.

стране предоставляется множество возможностей формировать свою пенсию, в том

числе хранить свои пенсионные сбережения в банках, делать пенсионные вклады. Рассмотрим более выгодные условия хранения таких вкладов.

в 60 000 рублей сроком на 2 года (730

дней). Банки предоставляют по несколько вкладов для пенсионеров. Но я рассмотрела только вклад «Пенсионный-плюс». Поэтому для начала выяснила, в каком из 2-ух банков вклад является наиболее выгодным.

По формуле сложных процентов Sn=S0 (1+0,01 р)n найдем сумму накопленных денежных средств за 2 года:
Вклад в РоссельхозБанке: S2= 60 000 (1+0,016,35)2 =67 861.93 (руб)
Вклад в Сбербанке: S2= 60 000 (1+0,013.5)2 =64 273,5(руб)

Так, доход по вкладу в РоссельхозБанке составит 7 861.93 рубля, а в Сбербанке – 4 273,5 рублей. Таким образом, вклад в РоссельхозБанке намного выгоднее вклада в Сбербанке.

когда залог, служащий основанием этого кредита, не передается кредитору,

а остается в собственности должника. На заложенное под ипотеку имущество налагается запрещение на продажу или переоформление его на другое лицо до полного погашения кредита и всех процентов.

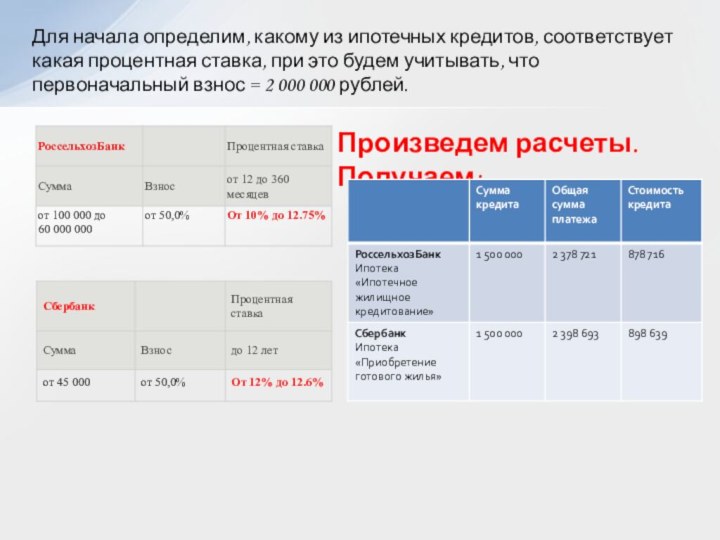
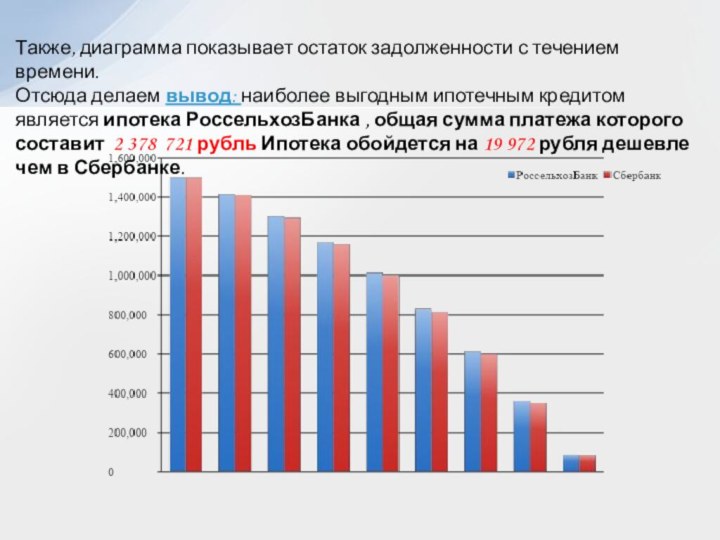
Предположим: Продав свой дом за 2 000 000 рублей, молодая семья хочет купить жильё за 3 500 000 рублей. Но денежных средств на приобретение недвижимости не хватает. Тогда семейная пара решается взять ипотеку 1 500 000 рублей сроком на 10 лет.
Стартовым этапом практически любой ипотеки является первоначальный взнос.

Первоначальный взнос - это часть стоимости жилья или какого-либо другого имущества, приобретаемого в кредит, которую заемщик должен иметь в наличии, чтобы получить кредит.

Нужно иметь ввиду: чем больше первоначальный взнос, тем больше возможностей, во-первых, вообще получить одобрение по кредиту, во вторых получить лучшие условия от банка по годовой процентной ставке.
Для подавляющего большинства банков первоначальный взнос по ипотеке является самым главным и принципиальным критерием первичного отсева заемщиков.

какая процентная ставка, при это будем учитывать, что первоначальный

взнос = 2 000 000 рублей.

Произведем расчеты. Получаем:

Отсюда делаем вывод: наиболее выгодным ипотечным кредитом является ипотека

РоссельхозБанка , общая сумма платежа которого составит 2 378 721 рубль Ипотека обойдется на 19 972 рубля дешевле чем в Сбербанке.

заинтересовавшими меня процентами в банковской сфере.
Узнала, что сейчас

область применения процентов очень велика по сравнению со временем их рождения, когда их применяли только ростовщики.
Я поняла, что проценты можно применять везде. И поэтому «Его величество ПРОЦЕНТ» существуют и уже никуда не денется.
Знание и понимание процентов необходимо в современной жизни.

Заключение.

Взял он фруктов, колбасы, Положил всё на весы. Продавец всё

подсчитала, Старика и обсчитала. В школе дед учился плохо, Не заметил он подвоха. Математику бы знал, Сохранил бы капитал!

К. Ларин