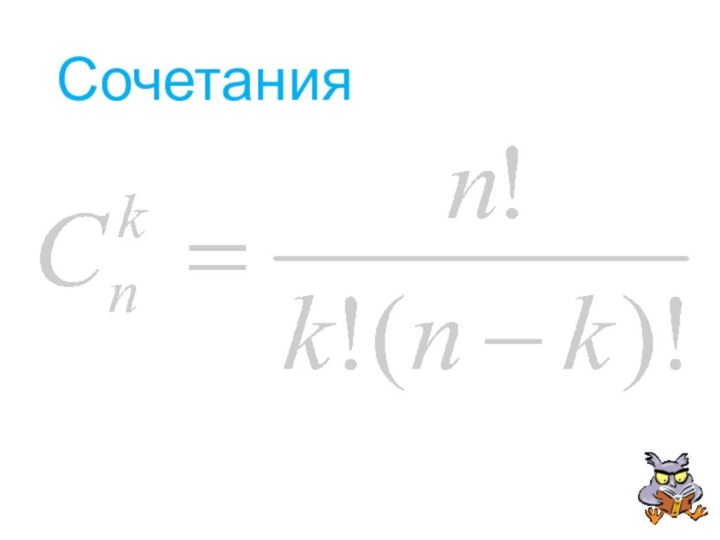краски из имеющихся пяти?».
Р е ш е н и
еОбозначим имеющиеся краски буквами латинского алфавита a, b, c, d, e. Выпишем возможные варианты смешивания красок, учитывая, что от порядка расположения красок результат не зависит:
abc, abd, abe, ace, ade,acd
bcd, bce, bde
cde
Мы указали различные способы смешивания красок, в которых по-разному сочетаются три краски из данных пяти. Говорят, что мы составили все возможные
сочетания из 5 элементов по 3.