- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2018 года по МАТЕМАТИКЕ
Содержание
- 2. Распределение тестовых баллов участников ЕГЭ по математике базового уровня в 2018, 2017 и 2016 гг.
- 3. Распределение участников экзамена по группамгруппа 1 –
- 4. Результаты выполнения заданий КИМ
- 5. ЕГЭ по математике профильного уровняВ 2018 г.
- 6. Результаты выполнения заданий КИМБолее 60% участников профильного
- 7. Существенно лучше результаты участников экзамена из группы
- 8. Рекомендации по совершенствованию преподавания математики с учетом
- 9. Важно также знать, что бесконечное решение задач,
- 10. Недостаток графических, геометрических представлений отражается и на
- 11. Скачать презентацию
- 12. Похожие презентации

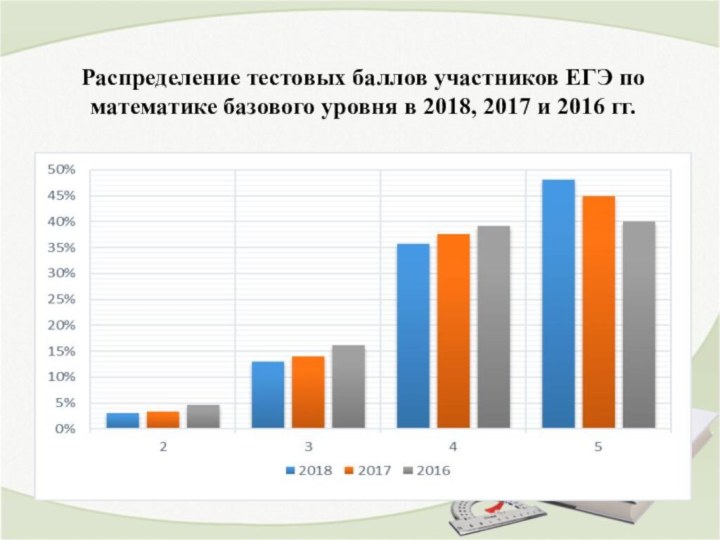









Слайд 2 Распределение тестовых баллов участников ЕГЭ по математике базового
уровня в 2018, 2017 и 2016 гг.
Слайд 3
Распределение участников экзамена по группам
группа 1 – от
0 до 6 баллов
«2»
группа 2 – от 7
до 11 баллов «3»
группа 3 – от 12 до 16 баллов
«4»
группа 4 – от 17 до 20 баллов
«5»
Слайд 4
Результаты выполнения заданий КИМ
Группа 3
Большую часть заданий
выполняют в диапазоне от 80% до 90%. Помимо заданий 13, 17 и 20, сложных и для более подготовленных участников, определенные трудности вызвали задания 14 (график функции), 15 (планиметрия), 16 (стереометрия), 19 (свойства чисел). Группа 4
Результат, близкий к максимальному или максимально возможный: они набрали от 17 до 20 баллов. В этой группе результаты выполнения почти всех заданий близки к 100%. Исключение составляют задания 13 (стереометрия) и 17 (решение неравенства) – их выполнили около 80%, а также задание 20 – выполнили около половины из участников этой группы.
Группа 1
75%- задания 11 и 12
Примерно 67% - задание 9
Около 50% - задания 6 и 18
21%-33% -задания 1и 4
10%-20% - задания2,3,5,7,8,14
Менее 10% - задания10,13,15,16,17,19,20.
Группа 2
Выше 80% - задания 9,11,12
50%-75% - задания 1,3,4,6,8, и 18
35%-50% - задания2,5,7,10,14
10%-25% -задания13,15,16,17,19,20
Наибольшие затруднения вызывают в этой группе геометрические задачи, логарифмические неравенства, свойства чисел.
Слайд 5
ЕГЭ по математике профильного уровня
В 2018 г. минимальный
балл не набрали 7,48% участников экзамена, в 2017 г.
– 14,35%, то есть этот показатель улучшился практически вдвое.
Слайд 6
Результаты выполнения заданий КИМ
Более 60% участников профильного экзамена
набрали от 6 до 11 первичных баллов (27–61 т.б.).
Это означает, что из первых 12 заданий базового и повышенного уровней с кратким ответом они выполнили не более 11 заданий. Так, они не смогли показать результат при выполнении даже одного из заданий повышенного уровня сложности с полным решением .С заданиями части 1 справляются 76–99% участников из этой группы, исключение составляют задания 7 (график производной) и 8 (стереометрия), с ними в этой группе справляются от трети до половины участников соответственно.
Из заданий части 2 наибольший результат был получен при выполнении задания 9 (преобразование степенных выражений) .
Задание 13 (решение тригонометрического уравнения) выполнили 7% выпускников из этой группы. С заданиями 14–19 в этой группе справились менее 1,5% участников.
Слайд 7 Существенно лучше результаты участников экзамена из группы с
хорошей подготовкой (12–19 п.б. / 62–80 т.б.). Они выполняют
задания 1–6, 9, 11 с результатом, близким к максимальному, задания 7, 8, 10, 12, 13 в диапазоне 75–90%; треть из этой группы справились с решением логарифмического неравенства (задание 15); четверть – со стереометрической задачей (задание 14). С наиболее сложными заданиями 16–19 эти участники справились в диапазоне 1,6–7%, при этом самым сложным оказалось задание 18 (система с параметром), а более простым – планиметрическая задача.Максимально возможные результаты группы высокобалльников очевидны. Как и в других группах, заметно небольшое снижение результатов по заданиям 7 и 8. Видимые различия начинаются с задания 14, с которым справились 81% участников этой группы, с заданием 15 – 87%, с заданием 16 – 53%, с заданием 17 – 49%, с заданием 18 – 31% и с заданием 19 – 26%.
Слайд 8 Рекомендации по совершенствованию преподавания математики с учетом результатов
ЕГЭ 2018 г.
Результаты экзамена, представленные
по группам, позволяют говорить о сложности заданий для экзаменуемых с тем или иным уровнем Поэтому так важно при обучении и подготовке к экзамену понимать те трудности, с которыми столкнутся обучающиеся, и работать дифференцированно, то есть с каждой группой учащихся отдельно. Задания по сложности должны быть адекватными для конкретной группы, то есть у учеников должен быть шанс и когнитивный ресурс выполнить задание, прибегнув к помощи учителя, одноклассников, справочников и прочих источников дополнительной информации. Что касается экзаменационных заданий, то лишена всякого смысла практика, когда ученику, который слабо справляется с заданиями части 1 экзамена профильного уровня, выдаются последние задания из части 2. Нужна грамотная диагностика уровня подготовки каждого ученика и обеспечение его именно теми заданиями, с которыми он, исходя из этого уровня, может справиться. Слайд 9 Важно также знать, что бесконечное решение задач, которые
ученик уже давно научился решать, также никак не повлияет
на качество его математической подготовки. Более того, натаскивание сыграет с ним злую шутку на экзамене – не позволит заметить незначительные изменения в условии задачи и скорректировать решение соответствующим образом. Именно это ярко отразилось на результатах выполнения задания 17 профильного варианта (экономическая задача) и является существенным фактором снижения процента участников, набравших полный балл за задание: увидев на известной позиции знакомую, как им показалось, задачу, многие участники не прочитали полностью и внимательно ее условие и допустили существенные ошибки, следуя «типовому алгоритму».Сложность задания относительна, следовательно, можно попытаться на нее влиять. Например, абстрактность задачи можно снизить, если использовать наглядные представления. Правда, именно с этим у большинства выпускников возникают проблемы. Результаты выполнения заданий как базового, так и профильного варианта экзамена говорят о недостатках в формировании пространственного мышления учащихся.
Прежде всего, это негативно отражается на решении стереометрических задач.
Слайд 10 Недостаток графических, геометрических представлений отражается и на результатах
выполнения заданий из других разделов курса математики, в частности
из математического анализа. Не более половины участников экзамена могут по графику производной найти точку экстремума (профильный экзамен) и по графику функции дать характеристику ее производной (базовый экзамен). Для этого необходимо также умение переформулировать условие с формального языка на графический и наоборот.Дело в том, что графические представления в данном случае тесно связаны с понятийной стороной вопроса о поведении функции и ее производной, именно поэтому целесообразно не натаскивать учащихся на каждое из данных заданий, а формировать общее понимание понятия производной функции, не забывать о содержательной стороне, переходя к алгоритмической, тем более что задачи на понимание смысла и применение производной функции ежегодно включаются в задания ЕГЭ по математике. Надо понимать, что представление о производной и ее применении к исследованию функций можно получить, основываясь преимущественно на наглядных представлениях о скорости, об изменении величины и о касательной к гладкой линии.