Слайд 2
Задача о школьной викторине
На школьной викторине участникам
предложили 20 вопросов. За правильный ответ ученику ставилось 12
очков, а за неправильный списывали 10 очков. Сколько правильных ответов дал один из учеников, если он ответил на все вопросы и набрал
86 очков.
Слайд 3
Решение
Всего 20 вопросов. Пусть х ответов было правильных,
тогда (20 – х) ответов неправильных.
12х – 10(20
– х) = 86,
х = 13
Ответ: 13 правильных
ответов.
Слайд 4
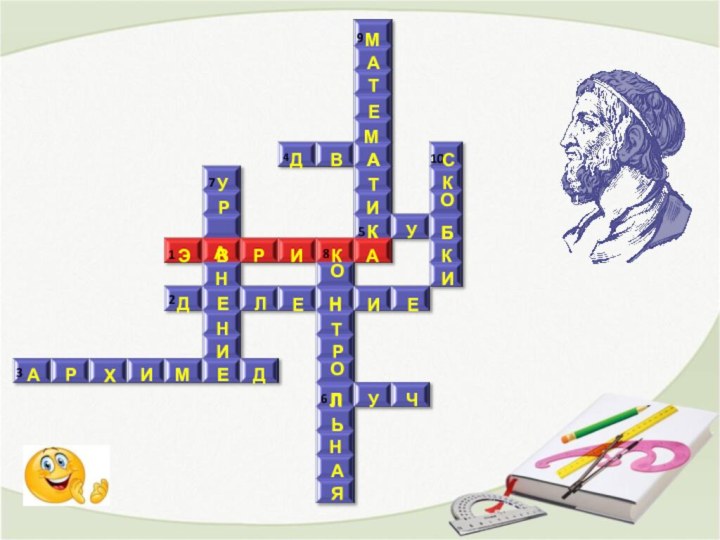
. Кроссворд «И в шутку, и всерьез»
По горизонтали:
1. ?.
2. Арифметическое действие.
3. Ученый – математик.
4. Самая нелюбимая оценка ученика.
5. Прямоугольный параллелепипед, у которого все ребра равны.
6. Геометрическая фигура, которая дружит с солнцем.
По вертикали:
7. Равенство, содержащее переменную.
8. Проверка учеников на выживание.
9. Ум в порядок приводит.
10. Забор для математических действий.
Слайд 7
Задача Синдбада
- морехода
Синдбад – мореход приплыл на остров. На
нем живут только правдолюбы ( они говорять только правду) и лжецы (они говорять только ложь). Синдбада сопровождал житель этого острова. Скоро они увидели еще одноо жителя. Синдбад послал своего сопровождающего узнать, кто этот житель – правдолюб или лжец. Сопровождающий вернулся и сказал, что тот говорит, что он лжец. Кем был сопровождающий –
правдолюб или лжец?
Слайд 8
Отгадка
Если житель был правдолюбом, то он об этом
сказал бы сопровождающему. Если бы житель был лжец, то
он тоже сказал бы, что он правдолюб. Таким образом, ответ о жителе – правдолюб. А сопровождающий сказал Синдбаду, что житель – лжец. Поэтому сопровождающий – лжец
Слайд 11
Кто сказал, что в науке поэзии нет?
Нужно
только понять и увидеть.
Художники – математики
Задача пиратов
Шесть пиратов захватили
Купеческое судно. Добыча была богатой – меньше чем сто одинаковых слитков золота. Начали пираты делить добычу, но один слиток оказался лишним. Пираты начали ссориться и в драке одного пирата убили. Снова стали делить добычу, но снова один слиток оказался лишним. Снова в драке погиб один пират. Так было до тех пор, пока в конце-концов остался только один пират, да и тот умер от ран. Сколько слитков было?
Слайд 14
Решение:
Если вначале было бы на один слиток
меньше, то деление состоялось бы. Число меньше 100, делящееся
на 2, 3, 4, 5, 6 – это число 60. Всего было 60+1=61 слиток золота.
Слайд 15
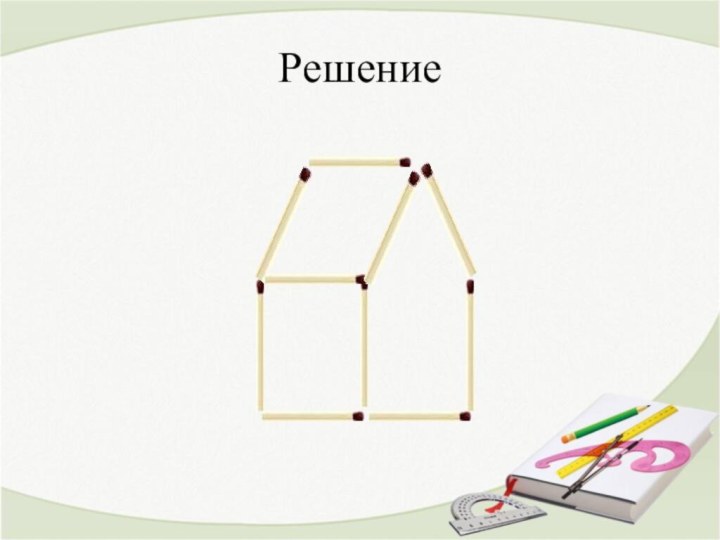
Из спичек построен дом. Переложите 2 спички так,
чтобы дом повернулся другой стороной.
Слайд 17
Задача 2
В бутылке, стакане, кувшине и банке находятся
молоко, лимонад, квас и вода. Известно, что вода и
молоко не в бутылке, сосуд с лимонадом стоит между кувшином и сосудом с квасом, в банке не лимонад и не вода. Стакан стоит около банки и сосуда с молоком. В какой сосуд налита каждая из жидкостей?
Слайд 18
Ответ
молоко в кувшине, лимонад в бутылке, квас
в банке,
вода в стакане.
Слайд 19
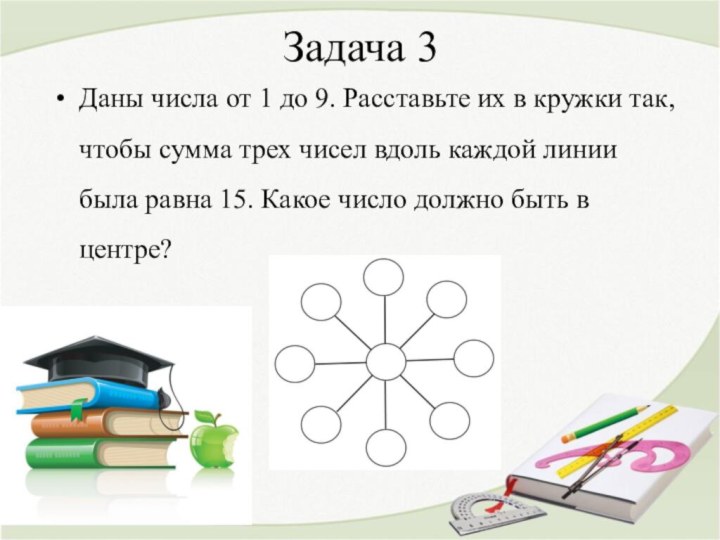
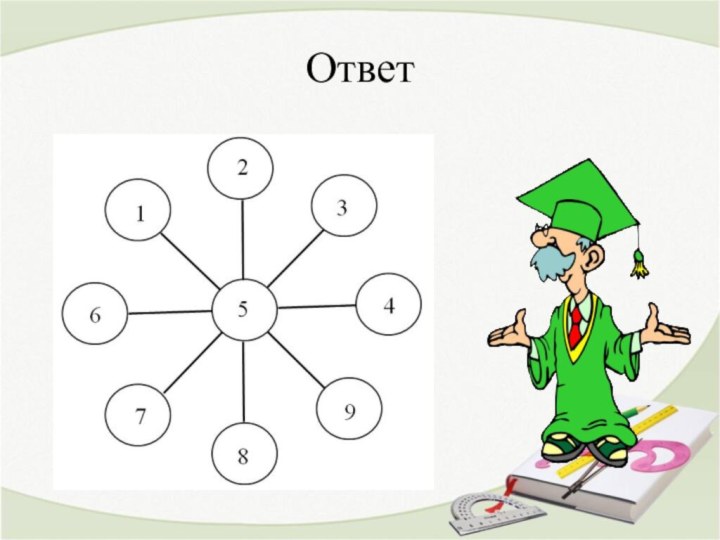
Задача 3
Даны числа от 1 до 9. Расставьте
их в кружки так, чтобы сумма трех чисел вдоль
каждой линии была равна 15. Какое число должно быть в центре?
Слайд 21
Задача на принцип Дирихле
В школе 33 класса,
1150 учеников. Найдется ли класс, в котором меньше 35
учеников?
Слайд 22
Решение
. Допустим, что во всех классах не менее
35 учеников, тогда во всей школе будет не менее
чем 35 ∙ 33 = 1155 (учеников), что противоречит условию задачи. Значит, в школе найдется класс, в котором менее чем 35 учеников.
Слайд 23
Еще один вопрос вопрос
Имеются две сковородки на которой
можно пожарить только один блин.
Какое минимальное время понадобиться
для обжаривания 3 блинов с двух сторон, если на обжаривание с одной стороны тратиться 1 минута?